Giải bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất.
Bác Dũng đầu tư không quá 1,2 tỉ đồng vào hai loại cổ phiếu: cổ phiếu A dự kiến chi trả cổ tức bằng tiền với tỉ lệ 5%; cổ phiếu B rủi ro cao hơn dự kiến chi trả cổ tức bằng tiền với tỉ lệ 12%. Giá cổ phiếu A là 30 000 đồng/1 cổ phiếu, giá cổ phiếu B là 40 000 đồng/1 cổ phiếu. Để giảm thiểu rủi ro, bác Dũng quyết định mua số lượng cổ phiếu B không quá 10 000 cổ phiếu. Hỏi bác Dũng nên đầu tư mỗi loại bao nhiêu cổ phiếu để lợi nhuận thu được là lớn nhất.
Đề bài
Bác Dũng đầu tư không quá 1,2 tỉ đồng vào hai loại cổ phiếu: cổ phiếu A dự kiến chi trả cổ tức bằng tiền với tỉ lệ 5%; cổ phiếu B rủi ro cao hơn dự kiến chi trả cổ tức bằng tiền với tỉ lệ 12%. Giá cổ phiếu A là 30 000 đồng/1 cổ phiếu, giá cổ phiếu B là 40 000 đồng/1 cổ phiếu. Để giảm thiểu rủi ro, bác Dũng quyết định mua số lượng cổ phiếu B không quá 10 000 cổ phiếu. Hỏi bác Dũng nên đầu tư mỗi loại bao nhiêu cổ phiếu để lợi nhuận thu được là lớn nhất.
Phương pháp giải - Xem chi tiết
Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:
Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình
\(\left\{ \begin{array}{l}{a_1}x + {b_1}y \le {c_1}\\{a_2}x + {b_2}y \le {c_2}\\...\\{a_k}x + {b_k}y \le {c_k}\end{array} \right.\)
Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.
Bước 3: Kết luận.
Lời giải chi tiết
Gọi \(x\) là số cổ phiếu A và \(y\) là số cổ phiếu B bác Dũng cần mua \((x \in N;y \in N)\)
Lợi nhuận bác Dũng thu được là \(T = 30000x.5\% + 40000y.12\% \) (đồng) hay \(T = 1500x + 4800y\) (đồng)
Khi đó, số tiền bác Dũng cần chi ra là \(30000x + 40000y\) (đồng)
Vì bác Dũng muốn đầu tư không quá 1,2 tỉ nên ta có \(30000x + 40000y \le 1200000000\) hay \(3x + 4y \le 120000.\)
Vì lượng cổ phiếu B không quá 10000 cổ phiếu nên ta có \(y \le 10000.\)
Để lợi nhuận thu được là lớn nhất ta có bài toán quy hoạch tuyến tính sau:
\(\left\{ \begin{array}{l}\max (T = 1500x + 4800y)\\3x + 4y \le 120000\\y \le 10000\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là các số thực) sau:
\(\left\{ \begin{array}{l}3x + 4y \le 120000\\y \le 10000\\x \ge 0\\y \ge 0\end{array} \right.\) (II)
 |
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 1500x + 4800y\) khi \((x,y)\) thoả mãn hệ bất phương trình (II).
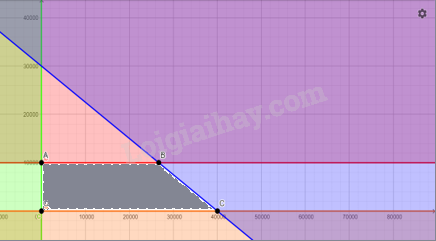
Bước 1. Xác định miền nghiệm của hệ bất phương trình (I)
Miền nghiệm là miền tứ giác OABC với toạ độ các đỉnh \(O(0;0);A(0;10000);\)\(B\left( {\frac{{80000}}{3};10000} \right);C(40000;0).\)
Bước 2. Tính giá trị biểu thức \(T(x,y) = 1500x + 4800y\) tại các đỉnh của tứ giác OABC: \(T(0;0) = 0;T(0;10000) = 48000000;\) \(T\left( {\frac{{80000}}{3};10000} \right) = 88000000;T(40000;0) = 60000000.\)
Bước 3. Ta đã biết biểu thức \(T = 1500x + 4800y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được ở bước 2 kết hợp với điều kiện \(x,y\) là các số tự nhiên ta được giá trị lớn nhất cần tìm là \(T(40000;0) = 60000000.\)
Vậy bác Dũng nên đầu tư mua 40 000 cổ phiếu loại A để thu được lợi nhuận lớn nhất.
Giải bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều: Tổng quan và Phương pháp giải
Bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn luyện và củng cố kiến thức về một chủ đề cụ thể. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững lý thuyết, hiểu rõ các công thức và phương pháp liên quan. Tusach.vn sẽ cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ cách tiếp cận và giải quyết bài toán.
Nội dung bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Bài 5 thường bao gồm các dạng bài tập sau:
- Dạng 1: Bài tập về... (Ví dụ: Giải phương trình, bất phương trình)
- Dạng 2: Bài tập về... (Ví dụ: Tìm giá trị lớn nhất, giá trị nhỏ nhất)
- Dạng 3: Bài tập về... (Ví dụ: Ứng dụng đạo hàm vào các bài toán thực tế)
Lời giải chi tiết bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Bài 5: (Đề bài cụ thể của bài 5 sẽ được trình bày ở đây)
Lời giải:
- Bước 1: Phân tích đề bài và xác định yêu cầu.
- Bước 2: Áp dụng kiến thức và công thức liên quan.
- Bước 3: Thực hiện các phép tính và biến đổi đại số.
- Bước 4: Kiểm tra lại kết quả và đưa ra kết luận.
(Giải thích chi tiết từng bước, kèm theo các ví dụ minh họa cụ thể)
Mẹo giải nhanh và hiệu quả
Để giải bài tập Toán 12 nhanh và hiệu quả, bạn nên:
- Nắm vững lý thuyết và công thức.
- Luyện tập thường xuyên với nhiều dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm giải toán.
- Tham khảo lời giải của các bài tập tương tự.
Lưu ý quan trọng
Khi giải bài tập Toán 12, bạn cần chú ý:
- Đọc kỹ đề bài và xác định đúng yêu cầu.
- Sử dụng đúng đơn vị đo.
- Kiểm tra lại kết quả trước khi đưa ra kết luận.
Tusach.vn - Đồng hành cùng bạn trên con đường học tập
Tusach.vn là website cung cấp tài liệu học tập, lời giải bài tập và các thông tin hữu ích cho học sinh, sinh viên. Chúng tôi luôn cố gắng cập nhật nội dung mới nhất và cung cấp dịch vụ tốt nhất cho người dùng. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Bảng tổng hợp các công thức liên quan (Ví dụ)
| Công thức | Mô tả |
|---|---|
| f'(x) | Đạo hàm của hàm số f(x) |
| ∫f(x)dx | Tích phân của hàm số f(x) |
Hy vọng với lời giải chi tiết và những chia sẻ trên, bạn đã hiểu rõ cách giải bài 5 trang 28 Chuyên đề học tập Toán 12 - Cánh diều. Chúc bạn học tập tốt!