Đề bài
Trong một phản ứng hoá học, lượng khí \({\rm{C}}{{\rm{O}}_{\rm{2}}}\) thoát ra \(V(t)\) được tính theo thời gian \(t\) bằng công thức:
\(V(t) = \frac{{0,2{k_1}}}{{{k_1} - {k_2}}}\left( {{e^{ - {k_2}t}} - {e^{ - {k_1}t}}} \right),\)
Trong đó \(V(t)\) được tính theo đơn vị mililít và \(t\) được tính theo đơn vị giây; \({k_1},{k_2}\) là các hằng số sao cho \({k_1} > {k_2} > 0\).
Lượng khí \({\rm{C}}{{\rm{O}}_{\rm{2}}}\) thoát ra trong phản ứng đó có giá trị lớn nhất là bao nhiêu?
Phương pháp giải - Xem chi tiết
+) Vẽ bảng biến thiên của hàm số \(V(t) = \frac{{0,2{k_1}}}{{{k_1} - {k_2}}}\left( {{e^{ - {k_2}t}} - {e^{ - {k_1}t}}} \right),\)với \(t \in (0; + \infty )\).
+) Ta sẽ tìm giá trị lớn nhất của hàm số \(V(t)\).
Lời giải chi tiết
Xét hàm số \(V(t) = \frac{{0,2{k_1}}}{{{k_1} - {k_2}}}\left( {{e^{ - {k_2}t}} - {e^{ - {k_1}t}}} \right),\) với \({k_1} > {k_2} > 0\) và \(t \in (0; + \infty )\).
Ta có \(V'(t) = \frac{{0,2{k_1}}}{{{k_1} - {k_2}}}\left( { - {k_2}{e^{ - {k_2}t}} + {k_1}{e^{ - {k_1}t}}} \right),\)
Do đó \(V'(t) = 0 \Leftrightarrow \frac{{0,2{k_1}}}{{{k_1} - {k_2}}}\left( { - {k_2}{e^{ - {k_2}t}} + {k_1}{e^{ - {k_1}t}}} \right) = 0 \Leftrightarrow {k_2}{e^{ - {k_2}t}} = {k_1}{e^{ - {k_1}t}}\)
\({e^{({k_2} - {k_1})t}} = \frac{{{k_2}}}{{{k_1}}} \Leftrightarrow ({k_2} - {k_1})t = ln\left( {\frac{{{k_2}}}{{{k_1}}}} \right) \Leftrightarrow t = \frac{{\ln \left( {\frac{{{k_2}}}{{{k_1}}}} \right)}}{{{k_2} - {k_1}}}.\)
Đặt \({t_0} = \frac{{\ln \left( {\frac{{{k_2}}}{{{k_1}}}} \right)}}{{{k_2} - {k_1}}}.\)
Ta có bảng biến thiên của hàm số
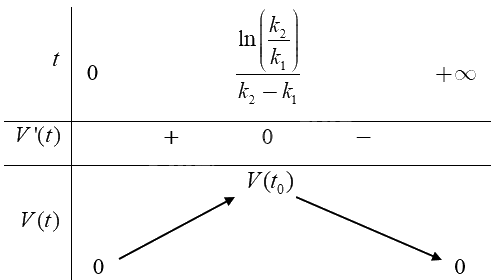
Căn cứ vào bảng biến thiên ta có \(\mathop {\max }\limits_{(0; + \infty )} = V({t_0}) = \frac{{0,2{k_1}}}{{{k_1} - {k_2}}}\left[ {{{\left( {\frac{{{k_2}}}{{{k_1}}}} \right)}^{\frac{{ - {k_2}}}{{{k_2} - {k_1}}}}} - {{\left( {\frac{{{k_2}}}{{{k_1}}}} \right)}^{\frac{{ - {k_1}}}{{{k_2} - {k_1}}}}}} \right]\) tại \(t = {t_0} = \frac{{\ln \left( {\frac{{{k_2}}}{{{k_1}}}} \right)}}{{{k_2} - {k_1}}}.\)
Vậy lượng khí \({\rm{C}}{{\rm{O}}_{\rm{2}}}\) thoát ra trong phản ứng đó có giá trị lớn nhất là \(\frac{{0,2{k_1}}}{{{k_1} - {k_2}}}\left[ {{{\left( {\frac{{{k_2}}}{{{k_1}}}} \right)}^{\frac{{ - {k_2}}}{{{k_2} - {k_1}}}}} - {{\left( {\frac{{{k_2}}}{{{k_1}}}} \right)}^{\frac{{ - {k_1}}}{{{k_2} - {k_1}}}}}} \right]\) (mililit).

