Giải mục 1 trang 13 Chuyên đề học tập Toán 12 - Cánh diều
Tổng quan nội dung
Giải mục 1 trang 13 Chuyên đề học tập Toán 12 - Cánh Diều
Tusach.vn cung cấp lời giải chi tiết và dễ hiểu cho mục 1 trang 13 trong Chuyên đề học tập Toán 12 của nhà xuất bản Cánh Diều. Bài giải được các giáo viên có kinh nghiệm biên soạn, đảm bảo tính chính xác và giúp học sinh hiểu rõ bản chất vấn đề.
Chúng tôi luôn cập nhật nhanh chóng và đầy đủ các bài giải Toán 12, hỗ trợ tối đa cho quá trình học tập của bạn.
Xét phép thử (T): “Một vận động viên bắn một phát súng vào mục tiêu”. Gọi (X) là số lần bắn trúng mục tiêu. Khi đó, (X) là biến ngẫu nhiên rời rạc nhận giá trị thuộc tập hợp ({ 0,1} ). Giả sử (P(X = 1) = p(0 < p < 1)). Suy ra (P(X = 0) = 1 - p). Lập bảng phân bố xác suất của biến ngẫu nhiêu rời rạc (X).
Hoạt động 1
Trả lời câu hỏi Hoạt động 1 trang 13 Chuyên đề học tập Toán 12 Cánh diều
Xét phép thử \(T\): “Một vận động viên bắn một phát súng vào mục tiêu”. Gọi \(X\) là số lần bắn trúng mục tiêu. Khi đó, \(X\) là biến ngẫu nhiên rời rạc nhận giá trị thuộc tập hợp \(\{ 0,1\} \).
Giả sử \(P(X = 1) = p(0 < p < 1)\). Suy ra \(P(X = 0) = 1 - p\).
Lập bảng phân bố xác suất của biến ngẫu nhiêu rời rạc \(X\).
Phương pháp giải:
+ Lập bảng phân bố xác suất với \(X\) nhận các giá trị 0,1
+ \(P(X = 1) = p\) ; \(P(X = 0) = 1 - p\)
Lời giải chi tiết:
Ta có \(P(X = 1) = p\) ; \(P(X = 0) = 1 - p\). Vậy biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
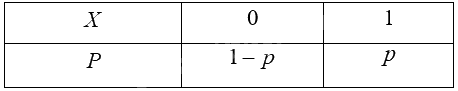
- Hoạt động 1
Trả lời câu hỏi Hoạt động 1 trang 13 Chuyên đề học tập Toán 12 Cánh diều
Xét phép thử \(T\): “Một vận động viên bắn một phát súng vào mục tiêu”. Gọi \(X\) là số lần bắn trúng mục tiêu. Khi đó, \(X\) là biến ngẫu nhiên rời rạc nhận giá trị thuộc tập hợp \(\{ 0,1\} \).
Giả sử \(P(X = 1) = p(0 < p < 1)\). Suy ra \(P(X = 0) = 1 - p\).
Lập bảng phân bố xác suất của biến ngẫu nhiêu rời rạc \(X\).
Phương pháp giải:
+ Lập bảng phân bố xác suất với \(X\) nhận các giá trị 0,1
+ \(P(X = 1) = p\) ; \(P(X = 0) = 1 - p\)
Lời giải chi tiết:
Ta có \(P(X = 1) = p\) ; \(P(X = 0) = 1 - p\). Vậy biến ngẫu nhiên rời rạc \(X\) có bảng phân bố xác suất như sau:
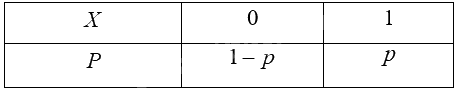
Giải mục 1 trang 13 Chuyên đề học tập Toán 12 - Cánh Diều: Hướng dẫn chi tiết và dễ hiểu
Chào mừng các em học sinh đến với phần giải bài tập mục 1 trang 13 Chuyên đề học tập Toán 12 - Cánh Diều. Đây là một phần quan trọng trong chương trình học, đòi hỏi các em phải nắm vững kiến thức nền tảng và kỹ năng giải quyết vấn đề. Tusach.vn sẽ đồng hành cùng các em để giải quyết những khó khăn trong quá trình học tập.
Nội dung chính của mục 1 trang 13
Mục 1 trang 13 Chuyên đề học tập Toán 12 - Cánh Diều thường tập trung vào một chủ đề cụ thể trong chương trình. Để giải quyết các bài tập trong mục này, các em cần:
- Nắm vững định nghĩa, tính chất và các công thức liên quan đến chủ đề.
- Hiểu rõ yêu cầu của từng bài tập.
- Áp dụng các kiến thức đã học để giải quyết bài tập một cách chính xác và hiệu quả.
Giải chi tiết các bài tập trong mục 1 trang 13
Dưới đây là giải chi tiết các bài tập trong mục 1 trang 13 Chuyên đề học tập Toán 12 - Cánh Diều:
Bài 1: (Ví dụ minh họa - cần thay thế bằng nội dung thực tế)
Đề bài: (Ví dụ: Tính đạo hàm của hàm số y = x^2 + 2x + 1)
Lời giải:
- Sử dụng quy tắc đạo hàm của tổng: (u + v)' = u' + v'
- Sử dụng quy tắc đạo hàm của lũy thừa: (x^n)' = nx^(n-1)
- Áp dụng các quy tắc trên để tính đạo hàm của từng thành phần trong hàm số.
- Kết hợp các kết quả để tìm đạo hàm của hàm số y = x^2 + 2x + 1.
Kết quả: y' = 2x + 2
Bài 2: (Ví dụ minh họa - cần thay thế bằng nội dung thực tế)
Đề bài: (Ví dụ: Tìm cực trị của hàm số y = x^3 - 3x + 2)
Lời giải:
- Tính đạo hàm bậc nhất y' của hàm số.
- Tìm các điểm cực trị bằng cách giải phương trình y' = 0.
- Xác định loại cực trị (cực đại hoặc cực tiểu) bằng cách sử dụng đạo hàm bậc hai y''.
- Tính giá trị của hàm số tại các điểm cực trị.
Kết quả: (Ví dụ: Hàm số đạt cực đại tại x = -1, giá trị cực đại là y = 4; Hàm số đạt cực tiểu tại x = 1, giá trị cực tiểu là y = 0)
Lưu ý khi giải bài tập
Để đạt kết quả tốt nhất khi giải bài tập mục 1 trang 13 Chuyên đề học tập Toán 12 - Cánh Diều, các em cần:
- Đọc kỹ đề bài và xác định rõ yêu cầu.
- Sử dụng các công thức và định lý một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
- Tham khảo các nguồn tài liệu khác để hiểu rõ hơn về chủ đề.
Tusach.vn – Người bạn đồng hành đáng tin cậy
Tusach.vn luôn nỗ lực cung cấp những lời giải chi tiết, chính xác và dễ hiểu nhất cho các em học sinh. Chúng tôi hy vọng rằng với sự hỗ trợ của Tusach.vn, các em sẽ học tập tốt hơn và đạt được những thành công trong học tập.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.
| Chủ đề | Liên kết |
|---|---|
| Giải Toán 12 Cánh Diều | https://tusach.vn/toan-12-canh-dieu |
| Chuyên đề học tập Toán 12 | https://tusach.vn/chuyen-de-toan-12 |