Giải bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất.
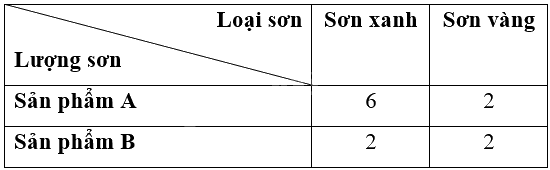
Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 3 (đơn vị: kg/1 sản phẩm). Người ta dự định sử dụng không quán 12 kg sơn xanh và không quá 8 kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Mỗi sản phẩm loại A lãi 10 triệu đồng và mỗi sản phẩm loại B lãi 8 triệu đồng. Tính khối lượng sản phẩm từng loại cần sơn sao cho số tiền lãi thu được là lớn nhất.
Đề bài
Người ta cần sơn hai loại sản phẩm A, B bằng hai loại sơn: sơn xanh, sơn vàng. Lượng sơn để sơn mỗi loại sản phẩm đó được cho ở Bảng 3 (đơn vị: kg/1 sản phẩm).
Người ta dự định sử dụng không quán 12 kg sơn xanh và không quá 8 kg sơn vàng để sơn tất cả các sản phẩm của hai loại đó. Mỗi sản phẩm loại A lãi 10 triệu đồng và mỗi sản phẩm loại B lãi 8 triệu đồng. Tính khối lượng sản phẩm từng loại cần sơn sao cho số tiền lãi thu được là lớn nhất.
Phương pháp giải - Xem chi tiết
Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:
Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình
\(\left\{ \begin{array}{l}{a_1}x + {b_1}y \le {c_1}\\{a_2}x + {b_2}y \le {c_2}\\...\\{a_k}x + {b_k}y \le {c_k}\end{array} \right.\)
Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.
Bước 3: Kết luận.
Lời giải chi tiết
Gọi \(x,y\) lần lượt là số sản phẩm loại A và loại B người đó cần sơn \((x \in N;y \in N)\)
Số tiền lãi người đó thu được là \(T = 10x + 8y\) (triệu đồng)
Vì người đó sử dụng không quá 12 kg sơn xanh nên ta có \(6x + 2y \le 12;\)
Vì người đó sử dụng không quá 8 kg sơn vàng nên ta có \(2x + 2y \le 8;\)
Do người đó muốn số tiền lãi thu được là lớn nhất nên ta có bài toán quy hoạch tuyến tính \(\left\{ \begin{array}{l}\max (T = 10x + 8y)\\6x + 2y \le 12\\2x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là số thực) sau:
\(\left\{ \begin{array}{l}6x + 2y \le 12\\2x + 2y \le 8\\x \ge 0\\y \ge 0\end{array} \right.\) (II)
 |
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 10x + 8y\) khi \((x,y)\) thoả mãn bất phương trình (II)
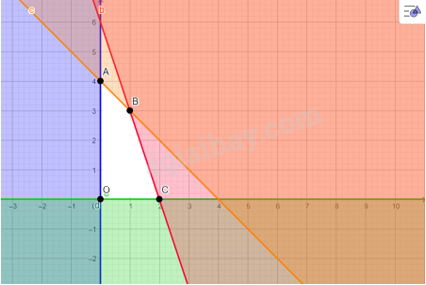
Bước 1. Xác định miền nghiệm của hệ bất phương trình (II)
Miền nghiệm là miền tứ giác OABC với toạ độ các đỉnh \(O(0;0);\) \(A(0;4);\) \(B(1;3)\); \(C(2;0).\)
Bước 2. Tính giá trị biểu thức \(T(x,y) = 10x + 8y\) tại các đỉnh của tứ giác này: \(T(0;0) = 0;\) \(T(0;4) = 32;\) \(T(1;3) = 34;\) \(T(2;0) = 20.\)
Bước 3. Ta đã biết biểu thức \(T = 10x + 8y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của \(T\) ở bước 2, ta được giá trị lớn nhất cần tìm là \(T(1;3) = 34.\)
Bước 4. Vì 1 và 3 đều là các số tự nhiên nên cặp số \((1;3)\) là nghiệm của bài toán (I).
Vậy để số tiền lãi thu được là lớn nhất thì cần sơn 1 sản phẩm loại A và 3 sản phẩm loại B.
Giải bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều: Tổng quan và Phương pháp giải
Bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về một chủ đề cụ thể. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững lý thuyết, hiểu rõ các công thức và phương pháp liên quan. Tusach.vn sẽ cung cấp lời giải chi tiết, từng bước, giúp bạn hiểu rõ cách tiếp cận và giải quyết bài toán.
Nội dung bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Bài 3 thường bao gồm các dạng bài tập sau:
- Dạng 1: Bài tập về... (Ví dụ: Giải phương trình, bất phương trình)
- Dạng 2: Bài tập về... (Ví dụ: Tìm giá trị lớn nhất, giá trị nhỏ nhất)
- Dạng 3: Bài tập về... (Ví dụ: Chứng minh bất đẳng thức)
Lời giải chi tiết bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều
Câu a: (Giả sử đây là nội dung câu a của bài 3)
Giải:
...
Câu b: (Giả sử đây là nội dung câu b của bài 3)
Giải:
...
Mẹo giải nhanh và hiệu quả
Để giải bài tập Toán 12 nhanh và hiệu quả, bạn nên:
- Đọc kỹ đề bài: Xác định rõ yêu cầu của bài toán.
- Xác định kiến thức cần sử dụng: Liên hệ bài toán với các kiến thức đã học.
- Lập kế hoạch giải: Xác định các bước cần thực hiện để giải bài toán.
- Kiểm tra lại kết quả: Đảm bảo kết quả của bạn là chính xác.
Ví dụ minh họa
Ví dụ: (Ví dụ về một bài tập tương tự)
Giải:
...
Luyện tập thêm
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập tương tự trong sách giáo khoa, sách bài tập hoặc trên các trang web học tập trực tuyến.
Bảng tổng hợp công thức liên quan
| Công thức | Mô tả |
|---|---|
| Công thức 1 | Giải thích công thức 1 |
| Công thức 2 | Giải thích công thức 2 |
Kết luận
Hy vọng với lời giải chi tiết và những hướng dẫn trên, bạn đã hiểu rõ cách giải bài 3 trang 28 Chuyên đề học tập Toán 12 - Cánh diều. Chúc bạn học tập tốt và đạt kết quả cao trong kỳ thi!
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục kiến thức. Hãy truy cập website của chúng tôi để xem thêm nhiều bài giải và tài liệu học tập hữu ích khác.