Giải Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 - Cánh diều
Tổng quan nội dung
Giải Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 - Cánh Diều
Tusach.vn cung cấp lời giải chi tiết và dễ hiểu cho Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12, bộ sách Cánh Diều. Bài giải được các giáo viên có kinh nghiệm biên soạn, đảm bảo tính chính xác và giúp học sinh nắm vững kiến thức.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, tusach.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán.
Một công ty kinh doanh đồ uống sản xuất hai loại nước sinh tố theo công thức sau: Trong 1 lít nước sinh tố loại thứ nhất có 0,7 lít nước anh đào; 0,3 lít nước cam và bán với giá là 24 000 đồng/lít. Trong 1 lít nước sinh tố loại thứ hai có 0,4 lít nước anh đào; 0,6 lít nước cam và bán với giá là 18 000 đồng/lít. Công ty có 120 lít nước anh đào và 150 lít nước cam. Hỏi công ty phải sản xuất bao nhiêu lít nước sinh tố mỗi loại sao cho tổng số tiền công ty thu được là nhiều nhất?
Hoạt động mở đầu
Trả lời câu hỏi Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 Cánh diều
Một công ty kinh doanh đồ uống sản xuất hai loại nước sinh tố theo công thức sau:
Trong 1 lít nước sinh tố loại thứ nhất có 0,7 lít nước anh đào; 0,3 lít nước cam và bán với giá là 24 000 đồng/lít.
Trong 1 lít nước sinh tố loại thứ hai có 0,4 lít nước anh đào; 0,6 lít nước cam và bán với giá là 18 000 đồng/lít.
Công ty có 120 lít nước anh đào và 150 lít nước cam.
Hỏi công ty phải sản xuất bao nhiêu lít nước sinh tố mỗi loại sao cho tổng số tiền công ty thu được là nhiều nhất?
Phương pháp giải:
Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:
Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình
\(\left\{ \begin{array}{l}{{a}_{1}}x+{{b}_{1}}y\le {{c}_{1}} \\{{a}_{2}}x+{{b}_{2}}y\le {{c}_{2}}\\...\\{{a}_{k}}x+{{b}_{k}}y\le {{c}_{k}}\end{array} \right.\)
Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.
Bước 3: Kết luận.
Lời giải chi tiết:
Gọi \(x,y\) lần lượt là số lít nước sinh tố loại thứ nhất và loại thứ hai mà công ty dự định sản xuất (\(x \ge 0;y \ge 0\))
Tổng số tiền công ty thu được khi bán \(x\) lít nước sinh tố loại thứ nhất và \(y\) lít nước sinh tố loại tứ hai là \(T = 24x + 18y\) (nghìn đồng).
Số lít nước anh đào có trong \(x\) lít nước sinh tố loại thứ nhất và có trong \(y\) lít nước sinh tố loại tứ hai là \(0,7x + 0,4y\) (lít)
Số lít nước anh cam có trong \(x\) lít nước sinh tố loại thứ nhất và có trong \(y\) lít nước sinh tố loại tứ hai là \(0,3x + 0,6y\) (lít)
Vì công ty có 120 lít nước anh đào và 150 lít nước cam nên lượng nguyên liệu sử dụng không vượt qua mức dự trữ trên do đó ta có hệ bất phương trình \(\left\{ \begin{array}{l}0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\end{array} \right.\)
Để tổng số tiền công ty thu được là nhiều nhất thì ta có bài toán quy hoạch tuyến tính sau: \(\left\{ \begin{array}{l}\max (T = 24x + 18y)\\0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là các số thực) sau:
\(\left\{ \begin{array}{l}0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\\x \ge 0\\y \ge 0\end{array} \right.\)(II) | 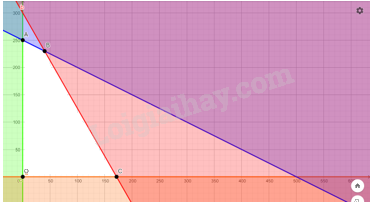 |
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 24x + 18y\) khi \((x,y)\) là nghiệm của hệ bất phương trình (II).
Bước 1. Xác định miền nghiệm của hệ bất phương trình (II)
Miền nghiệm là miền tứ giác OABC với \(O(0;0);\) \(A(0;250);\) \(B(40;230)\); \(C\left( {\frac{{1200}}{7};0} \right)\)
Bước 2. Tính giá trị biểu thức \(T(x,y) = 24x + 18y\) tại các đỉnh của tứ giác này: \(T(0;0) = 0;\) \(T(0;250) = 4500;\) \(T(40;230) = 5100;\) \(T\left( {\frac{{1200}}{7};0} \right) = \frac{{28800}}{7}.\)
Bước 3. Ta đã biết biểu thức \(T = 10x + 8y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của \(T\) ở bước 2, ta được giá trị lớn nhất cần tìm là \(T(40;230) = 5100\)
Bước 4. Vì 40 và 230 đều thỏa mãn yêu cầu bài toán nên nên cặp số \((40;230)\) là nghiệm của bài toán (I).
Vậy để số công ty thu được nhiều tiền nhất thì cần sản xuất 40 lít nước loại thứ nhất và 230 lít nước loại thứ hai.
- Hoạt động mở đầu
Trả lời câu hỏi Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 Cánh diều
Một công ty kinh doanh đồ uống sản xuất hai loại nước sinh tố theo công thức sau:
Trong 1 lít nước sinh tố loại thứ nhất có 0,7 lít nước anh đào; 0,3 lít nước cam và bán với giá là 24 000 đồng/lít.
Trong 1 lít nước sinh tố loại thứ hai có 0,4 lít nước anh đào; 0,6 lít nước cam và bán với giá là 18 000 đồng/lít.
Công ty có 120 lít nước anh đào và 150 lít nước cam.
Hỏi công ty phải sản xuất bao nhiêu lít nước sinh tố mỗi loại sao cho tổng số tiền công ty thu được là nhiều nhất?
Phương pháp giải:
Đưa bài toán về bài toán quy hoạch tuyến tính sau đó giải bài toán quy hoạch tuyến tính theo các bước sau:
Bước 1: Xác định miền nghiệm \((S)\) của hệ bất phương trình
\(\left\{ \begin{array}{l}{{a}_{1}}x+{{b}_{1}}y\le {{c}_{1}} \\{{a}_{2}}x+{{b}_{2}}y\le {{c}_{2}}\\...\\{{a}_{k}}x+{{b}_{k}}y\le {{c}_{k}}\end{array} \right.\)
Bước 2: Trong tất cả các điểm thuộc \((S)\) tìm điểm \((x,y)\) sao cho biểu thức \(T(x,y)\) có giá trị lớn nhất hoặc nhỏ nhất.
Bước 3: Kết luận.
Lời giải chi tiết:
Gọi \(x,y\) lần lượt là số lít nước sinh tố loại thứ nhất và loại thứ hai mà công ty dự định sản xuất (\(x \ge 0;y \ge 0\))
Tổng số tiền công ty thu được khi bán \(x\) lít nước sinh tố loại thứ nhất và \(y\) lít nước sinh tố loại tứ hai là \(T = 24x + 18y\) (nghìn đồng).
Số lít nước anh đào có trong \(x\) lít nước sinh tố loại thứ nhất và có trong \(y\) lít nước sinh tố loại tứ hai là \(0,7x + 0,4y\) (lít)
Số lít nước anh cam có trong \(x\) lít nước sinh tố loại thứ nhất và có trong \(y\) lít nước sinh tố loại tứ hai là \(0,3x + 0,6y\) (lít)
Vì công ty có 120 lít nước anh đào và 150 lít nước cam nên lượng nguyên liệu sử dụng không vượt qua mức dự trữ trên do đó ta có hệ bất phương trình \(\left\{ \begin{array}{l}0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\end{array} \right.\)
Để tổng số tiền công ty thu được là nhiều nhất thì ta có bài toán quy hoạch tuyến tính sau: \(\left\{ \begin{array}{l}\max (T = 24x + 18y)\\0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\\x \ge 0\\y \ge 0\end{array} \right.\) (I)
Xét hệ bất phương trình bậc nhất hai ẩn (\(x,y\) là các số thực) sau:
\(\left\{ \begin{array}{l}0,7x + 0,3y \le 120\\0,3x + 0,6y \le 150\\x \ge 0\\y \ge 0\end{array} \right.\)(II) | 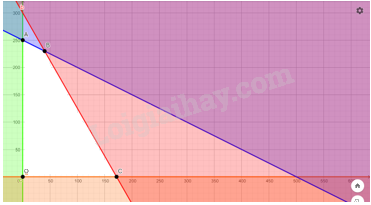 |
Ta cần tìm giá trị lớn nhất của biểu thức \(T = 24x + 18y\) khi \((x,y)\) là nghiệm của hệ bất phương trình (II).
Bước 1. Xác định miền nghiệm của hệ bất phương trình (II)
Miền nghiệm là miền tứ giác OABC với \(O(0;0);\) \(A(0;250);\) \(B(40;230)\); \(C\left( {\frac{{1200}}{7};0} \right)\)
Bước 2. Tính giá trị biểu thức \(T(x,y) = 24x + 18y\) tại các đỉnh của tứ giác này: \(T(0;0) = 0;\) \(T(0;250) = 4500;\) \(T(40;230) = 5100;\) \(T\left( {\frac{{1200}}{7};0} \right) = \frac{{28800}}{7}.\)
Bước 3. Ta đã biết biểu thức \(T = 10x + 8y\) đạt giá trị lớn nhất tại cặp số thực \((x,y)\) là toạ độ một trong các đỉnh của tứ giác OABC. So sánh bốn giá trị thu được của \(T\) ở bước 2, ta được giá trị lớn nhất cần tìm là \(T(40;230) = 5100\)
Bước 4. Vì 40 và 230 đều thỏa mãn yêu cầu bài toán nên nên cặp số \((40;230)\) là nghiệm của bài toán (I).
Vậy để số công ty thu được nhiều tiền nhất thì cần sản xuất 40 lít nước loại thứ nhất và 230 lít nước loại thứ hai.
Giải Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 - Cánh Diều: Hướng dẫn chi tiết và dễ hiểu
Hoạt động mở đầu trang 20 trong Chuyên đề học tập Toán 12 Cánh Diều đóng vai trò quan trọng trong việc khơi gợi hứng thú học tập và giúp học sinh tiếp cận kiến thức mới một cách tự nhiên. Hoạt động này thường đặt ra một tình huống thực tế hoặc một câu hỏi gợi mở, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết. Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho hoạt động này, giúp các em học sinh hiểu rõ bản chất vấn đề và tự tin hơn trong quá trình học tập.
Nội dung chính của Hoạt động mở đầu trang 20
Hoạt động mở đầu trang 20 thường tập trung vào việc ôn lại kiến thức cũ, chuẩn bị cho việc học các khái niệm mới trong chuyên đề. Cụ thể, hoạt động này có thể yêu cầu học sinh:
- Nhắc lại các định nghĩa, tính chất, công thức đã học.
- Giải các bài tập vận dụng kiến thức cũ.
- Phân tích một tình huống thực tế liên quan đến kiến thức đã học.
Lời giải chi tiết Hoạt động mở đầu trang 20
Để giúp học sinh hiểu rõ hơn về cách giải Hoạt động mở đầu trang 20, tusach.vn xin trình bày lời giải chi tiết như sau:
(Giải thích chi tiết từng bước giải, kèm theo hình ảnh minh họa nếu cần thiết. Ví dụ:)
- Bước 1: Phân tích đề bài và xác định yêu cầu.
- Bước 2: Vận dụng kiến thức đã học để giải quyết bài toán.
- Bước 3: Kiểm tra lại kết quả và đưa ra kết luận.
Tại sao nên tham khảo lời giải tại tusach.vn?
Tusach.vn là một website học tập uy tín, cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 12 Cánh Diều. Khi tham khảo lời giải tại tusach.vn, học sinh sẽ nhận được những lợi ích sau:
- Lời giải được biên soạn bởi các giáo viên có kinh nghiệm.
- Giải thích chi tiết từng bước giải, giúp học sinh hiểu rõ bản chất vấn đề.
- Có hình ảnh minh họa trực quan, giúp học sinh dễ dàng hình dung bài toán.
- Cập nhật lời giải mới nhất, đảm bảo tính chính xác và phù hợp với chương trình học.
Mở rộng kiến thức và luyện tập thêm
Sau khi đã nắm vững lời giải Hoạt động mở đầu trang 20, học sinh nên luyện tập thêm các bài tập tương tự để củng cố kiến thức. Tusach.vn cung cấp một kho bài tập Toán 12 Cánh Diều phong phú, đa dạng, giúp học sinh rèn luyện kỹ năng giải toán và chuẩn bị tốt cho các kỳ thi.
Bảng tổng hợp các chuyên đề Toán 12 Cánh Diều:
| Chuyên đề | Số trang |
|---|---|
| Đạo hàm | 100 |
| Tích phân | 80 |
| Số phức | 60 |
| Nguồn: tusach.vn | |
Hy vọng rằng lời giải Hoạt động mở đầu trang 20 Chuyên đề học tập Toán 12 Cánh Diều của tusach.vn sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!