Giải bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều
Tổng quan nội dung
Giải bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều
Tusach.vn xin giới thiệu lời giải chi tiết bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
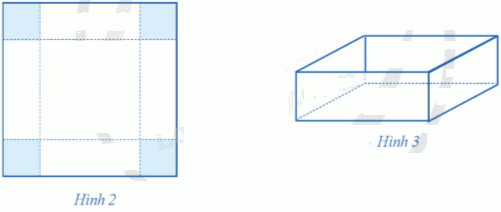
Bạn Hà có một tấm bìa hình vuông cạnh 60 cm (Hình 2). Bạn muốn làm một cái hộp đựng đồ có dạng hình hộp chữ nhật mà có thể để được vào một ngăn sách có dạng hình hộp chữ nhật, đáy là hình vuông cạnh 37 cm, chiều cao bằng 28 cm. Bạn cắt bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng (x) (cm), rồi gập lại thành một cái hộp không nắp (Hình 3). Tìm số nguyên dương (x) để làm được cái hộp đựng đồ có thể tích lớn nhất.
Đề bài
Bạn Hà có một tấm bìa hình vuông cạnh 60 cm (Hình 2). Bạn muốn làm một cái hộp đựng đồ có dạng hình hộp chữ nhật mà có thể để được vào một ngăn sách có dạng hình hộp chữ nhật, đáy là hình vuông cạnh 37 cm, chiều cao bằng 28 cm. Bạn cắt bốn góc của tấm bìa đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\) (cm), rồi gập lại thành một cái hộp không nắp (Hình 3). Tìm số nguyên dương \(x\) để làm được cái hộp đựng đồ có thể tích lớn nhất.
Phương pháp giải - Xem chi tiết
Thiết lập hàm số tính thể tích hộp và tìm giá trị lớn nhất của hàm số đó.
Lời giải chi tiết
Cạnh đáy hình vuông của chiếc hộp không nắp là \(60 - 2x\) (cm).
Khi đó ta có \(60 - 2x \le 37\) hay \(x \ge 11,5.\)
Chiều cao của chiếc hộp không nắp là \(x\) (cm). Khi đó ta có \(x \le 28.\)
Diện tích đáy của chiếc hộp không nắp là \({(60 - 2x)^2}\) (\({\rm{c}}{{\rm{m}}^{\rm{2}}}\)).
Thể tích của chiếc hộp không nắp là \(x{(60 - 2x)^2} = x(3600 - 240x + 4{x^2}) = 3600x - 240{x^2} + 4{x^3}\) (\({\rm{c}}{{\rm{m}}^{\rm{3}}}\)).
Xét hàm số \(f(x) = 3600x - 240{x^2} + 4{x^3}\) với \(11,5 \le x \le 28.\)
Ta có \(f'(x) = 3600 - 480x + 12{x^2}.\)
Xét \(f'(x) = 0 \Leftrightarrow 3600 - 480x + 12{x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10(ktm)\\x = 30(ktm)\end{array} \right.\)
Ta có bảng biến thiên:
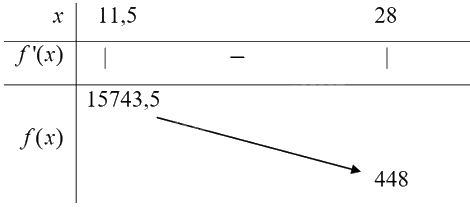
Căn cứ vào yêu cầu bài toán ta có \(\mathop {\max }\limits_{(0; + \infty )} f(x) = f(11,5) = 15743,5\) tại \(x = 11,5.\)
Vậy \(x = 11,5\) thì cái hộp có thể tích lớn nhất.
Giải bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều: Tổng quan và Phương pháp giải
Bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều thuộc chương trình học Toán 12, tập trung vào việc ôn tập và củng cố kiến thức về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các công thức đạo hàm cơ bản, quy tắc tính đạo hàm của hàm số hợp, hàm ẩn và các ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Nội dung chi tiết bài 1 trang 35
Bài 1 thường bao gồm các dạng bài tập sau:
- Tính đạo hàm của hàm số: Yêu cầu tính đạo hàm của các hàm số đơn thức, đa thức, hàm lượng giác, hàm mũ, hàm logarit và các hàm số phức tạp hơn.
- Áp dụng quy tắc đạo hàm: Vận dụng quy tắc đạo hàm của hàm hợp, đạo hàm của hàm ẩn, đạo hàm của hàm số lượng giác ngược.
- Giải phương trình đạo hàm: Tìm nghiệm của phương trình đạo hàm để xác định các điểm cực trị, điểm uốn của đồ thị hàm số.
- Ứng dụng đạo hàm: Sử dụng đạo hàm để khảo sát sự biến thiên của hàm số, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Lời giải chi tiết bài 1 trang 35 (Cánh diều)
Dưới đây là lời giải chi tiết cho từng phần của bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều:
Câu a:
Đề bài: Tính đạo hàm của hàm số f(x) = x3 - 2x2 + 5x - 1.
Lời giải:
f'(x) = 3x2 - 4x + 5
Câu b:
Đề bài: Tính đạo hàm của hàm số g(x) = sin(2x + 1).
Lời giải:
g'(x) = cos(2x + 1) * 2 = 2cos(2x + 1)
Câu c:
Đề bài: Tìm đạo hàm của hàm số y = ex * cos(x).
Lời giải:
y' = ex * cos(x) + ex * (-sin(x)) = ex(cos(x) - sin(x))
Mẹo giải nhanh và hiệu quả
Để giải nhanh và hiệu quả các bài tập về đạo hàm, bạn nên:
- Nắm vững các công thức đạo hàm cơ bản: Đạo hàm của các hàm số đơn thức, đa thức, hàm lượng giác, hàm mũ, hàm logarit.
- Thành thạo các quy tắc đạo hàm: Quy tắc đạo hàm của hàm hợp, đạo hàm của hàm ẩn, đạo hàm của hàm số lượng giác ngược.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài tập và rèn luyện kỹ năng giải toán.
- Sử dụng máy tính bỏ túi: Máy tính bỏ túi có thể giúp bạn tính toán nhanh chóng và chính xác các giá trị đạo hàm.
Tài liệu tham khảo hữu ích
Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
- Các trang web học Toán trực tuyến: Tusach.vn, Vietjack, Hoc24,...
- Các video bài giảng trên YouTube: Các kênh dạy Toán uy tín.
- Các diễn đàn Toán học: Nơi bạn có thể trao đổi kiến thức và kinh nghiệm với các bạn học khác.
Kết luận
Hy vọng với lời giải chi tiết và các mẹo giải nhanh trên, các bạn học sinh đã có thể tự tin giải bài 1 trang 35 Chuyên đề học tập Toán 12 - Cánh diều. Chúc các bạn học tập tốt và đạt kết quả cao trong kỳ thi!