Đề thi học kì 2 Toán 11 Cánh diều - Đề số 4
Tổng quan nội dung
Đề thi học kì 2 Toán 11 Cánh diều - Đề số 4
Tusach.vn xin giới thiệu Đề thi học kì 2 Toán 11 Cánh diều - Đề số 4, một tài liệu ôn tập quan trọng dành cho học sinh lớp 11. Đề thi này được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, giúp học sinh rèn luyện kỹ năng giải quyết vấn đề và củng cố kiến thức đã học.
Đề bài
Tính giá trị của biểu thức \(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}}\):
- A.\(288\)
- B.\(\frac{{32}}{9}\)
- C.\(\frac{2}{9}\)
- D.\(18\)
Trong các hình sau, hình nào là dạng đồ thị của hàm số\(y = {\log _a}x,0 < a < 1\)
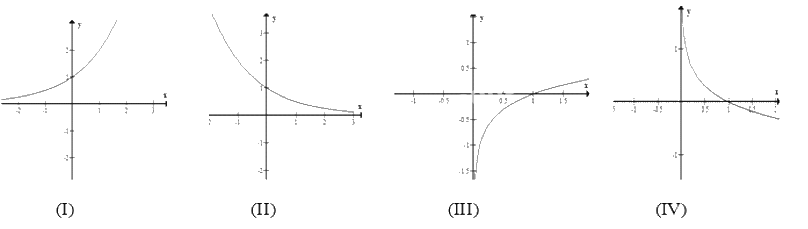
- A.(I).
- B.
(II).
- C.(IV).
- D.(III).
Cho hình chóp \(SABC\) có \(SA \bot \left( {ABC} \right).\) Gọi \(H,{\rm{ }}K\) lần lượt là trực tâm các tam giác \(SBC\) và\(ABC\). Mệnh đề nào sai trong các mệnh đề sau?
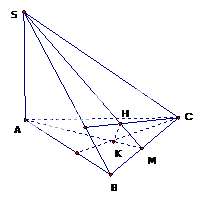
- A.\(BC \bot \left( {SAH} \right).\)
- B.\(HK \bot \left( {SBC} \right).\)
- C.\(BC \bot \left( {SAB} \right).\)
- D.
\(SH,{\rm{ }}AK{\rm{ }} , {\rm{ }}BC\) đồng quy tại một điểm
Cho tứ diện SABC trong đó SA, SB, SC vuông góc với nhau từng đôi một và SA = 3a, SB = a, SC = 2a. Khoảng cách từ A đến BC bằng?
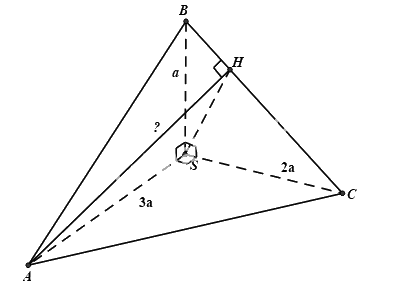
- A.
\(\frac{{3a\sqrt 2 }}{2}\).
- B.
\(\frac{{7a\sqrt 5 }}{5}\).
- C.
\(\frac{{8a\sqrt 3 }}{3}\).
- D.
\(\frac{{5a\sqrt 6 }}{6}\).
Tại một cuộc hội thảo quốc tế có 50 nhà khoa học trong đó có 31 người thành thạo tiếng Anh, 21 người thành thạo tiếng Pháp và 5 người thành thạo cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một người dự hội thảo. Xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là:
- A.\(\frac{{47}}{{50}}\)
- B.\(\frac{{37}}{{50}}\)
- C.\(\frac{{39}}{{50}}\)
- D.\(\frac{{41}}{{50}}\)
Cho hàm số \(y = - {x^3} + 3x - 2\) có đồ thị \(\left( C \right).\)Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung là
- A.\(y = - 2x + 1\)
- B.\(y = 2x + 1\)
- C.\(y = 3x - 2\)
- D.\(y = - 3x - 2\)
Cho hàm số \(y = {\sin ^2}x\). Khi đó đạo hàm y’ là
- A.\(y' = {\cos ^2}x\)
- B.\(y' = \sin 2x\)
- C.\(y' = \frac{{ - 3}}{{{{\sin }^2}x}} + 1\)
- D.\(y' = \frac{3}{{{{\sin }^2}x}}\)
Hàm số \(y = \sqrt {2 + 2{x^2}} \)có đạo hàm \(y' = \frac{{a + bx}}{{\sqrt {2 + 2{x^2}} }}\). Khi đó \(S = a - 2b\) có kết quả bằng
- A.\(S = - 4\)
- B.\(S = 10\)
- C.\(S = - 6\)
- D.\(S = 8\)
Hàm số \(y = \frac{{{x^2} + x}}{{x - 1}}\)có đạo hàm \(y' = \frac{{a{x^2} + bx + c}}{{{{(x - 1)}^2}}}\). Khi đó \(S = a + b + c\) có kết quả là:
- A.1
- B.2
- C.5
- D.2
Một chất điểm chuyển động có phương trình \(s\left( t \right) = {t^2} + 1\) (\(t\) tính bằng giây, \(s\) tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng
- A.\(1m/s.\)
- B.\(6m/s.\)
- C.\(4m/s.\)
- D.\(0m/s.\)
Hai người cùng bắn vào 1 bia. Người thứ nhất có xác suất bắn trúng là 60%, xác suất bắn trúng của người thứ 2 là 70%. Xác suất để cả hai người cùng bắn trật bằng:
- A.0,56
- B.0,21
- C.0,42
- D.0,48
Hàm số \(y = {x^5}\) có đạo hàm là:
- A.\(y' = 5{x^6}\)
- B.\(y' = 4{x^5}\)
- C.\(y' = 5x\)
- D.\(y' = 5{x^4}\)
Cho mẫu số liệu về thời gian (phút) đi từ nhà đến trường của một số học sinh như sau:

a) Cỡ mẫu của mẫu số liệu = 40
b) Mốt của mẫu số liệu thuộc nhóm \(\left[ {20;25} \right)\)
c) Mốt của mẫu số liệu thuộc nhóm \(\left[ {30;35} \right)\)
d) Mốt của mẫu số liệu là \({M_0} = 22,08\)
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x + 1}}{{3x}}(C)\)
a) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Oy là: \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Ox là là\(y = - \frac{1}{3}x - \frac{1}{3}\)
c) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) tại giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là: \(y = - 3x + \frac{7}{3}\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = - \frac{1}{3}\) là \(y = - \frac{1}{3}x + 1\) và \(y = - \frac{1}{3}x - \frac{1}{3}\)
Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm của cạnh BC. AH, IJ là đường cao tam giác AID.
a) \(BC \bot (AID)\)
b) \(AH \bot (BCD)\)
c) IJ là đường vuông góc chung của AD và BC
d) H là trọng tâm tam giác BCD
Trong đợt kiểm tra cuối học kì II lớp 11 của các trường trung học phổ thông, thống kê cho thấy có 93% học sinh tỉnh X đạt yêu cầu; 87% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y. Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập
a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là\(0,7809\)
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là \(0,0091\)
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là \(0,1818\)
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là \(0,9909\)
Tính giới hạn: \(I = \mathop {lim}\limits_{x \to - 3} \frac{{{x^2} + 2x - 3}}{{{x^2} + 5x + 6}}\)
Cho hàm số : \(y = 5{x^4} - 3{x^3} + 6x - \sqrt 7 \). Tính \(f'\left( 0 \right)\).
Cho hình chóp tứ giác đều\(S.ABCD\)có tất cả các cạnh bằng \(a\). Tính khoảng cách từ đỉnh \(S\) đến mặt phẳng \((ABCD).\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\).Cạnh bên \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\sqrt 2 \).Góc giữa đường thẳng \(SC\)và mặt phẳng \(\left( {ABCD} \right)\)bằng
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) với \(a,b,c \in \mathbb{R}\). Biết rằng đồ thị hàm số đi qua hai điểm \(A\left( {1; - 3} \right)\) và \(B\left( {2;3} \right)\), đồng thời tiếp tuyến của đồ thị tại điểm có hoành độ bằng \( - 1\) có hệ số góc bằng 2. Tính tổng \(S = a + b + c\).
Cho hàm số \(y = \frac{{x - 2}}{{x + 3}}\) có đồ thị \(\left( C \right).\) Tìm điểm \(M\) trên đồ thị \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)tạo với hai trục tọa độ một tam giác có diện tích bằng \(\frac{{18}}{5}.\)
Lời giải và đáp án
Tính giá trị của biểu thức \(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}}\):
- A.\(288\)
- B.\(\frac{{32}}{9}\)
- C.\(\frac{2}{9}\)
- D.\(18\)
Đáp án : B
Sử dụng công thức lũy thừa
\(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}} = \frac{{{4^{5 + \sqrt 3 }}{{.3}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}} = \frac{{{2^{10 + 2\sqrt 3 }}{{.3}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}} = \frac{{{2^5}}}{{{3^2}}} = \frac{{32}}{9}\)
Đáp án B.
Trong các hình sau, hình nào là dạng đồ thị của hàm số\(y = {\log _a}x,0 < a < 1\)
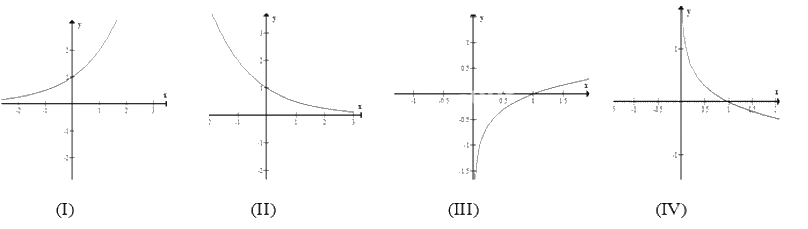
- A.(I).
- B.
(II).
- C.(IV).
- D.(III).
Đáp án : B
Hàm số \(y = {\log _a}x\) có đồ thị luôn đi qua điểm (1;0) và nghịch biến khi 0 <a<1
Do 0<a<1 nên đồ thị hàm số có chiều đi xuống từ trái qua phải
Đồ thị luôn đi qua điểm (1;0)
Đáp án B.
Cho hình chóp \(SABC\) có \(SA \bot \left( {ABC} \right).\) Gọi \(H,{\rm{ }}K\) lần lượt là trực tâm các tam giác \(SBC\) và\(ABC\). Mệnh đề nào sai trong các mệnh đề sau?
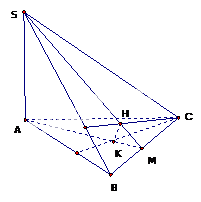
- A.\(BC \bot \left( {SAH} \right).\)
- B.\(HK \bot \left( {SBC} \right).\)
- C.\(BC \bot \left( {SAB} \right).\)
- D.
\(SH,{\rm{ }}AK{\rm{ }} , {\rm{ }}BC\) đồng quy tại một điểm
Đáp án : C
Sử dụng định lý đường thẳng vuông góc mặt phẳng
a)
\(\left\{ \begin{array}{l}BC \bot SA\,\,(Do\,\,SA \bot (ABC))\\BC \bot SH\\SA,SH \subset (SAH)\\SA \cap SH\end{array} \right. \Rightarrow BC \bot (SAH)\)
b)\(\left\{ \begin{array}{l}CK \bot SA\,\,\\CK \bot AB\\SA,AB \subset (SAB)\\SA \cap AB\end{array} \right. \Rightarrow CK \bot (SAB) \Rightarrow CK \bot SB\)
Lại có: \(\left\{ \begin{array}{l}SB \bot CK - cmt\,\,\\SB \bot CH\\CH,CK \subset (CKH)\\CH \cap CK\end{array} \right. \Rightarrow SB \bot (CKH) \Rightarrow SB \bot HK\)
Ta có: \(\left\{ \begin{array}{l}HK \bot SB - cmt\,\,\\HK \bot BC\,(Do\,BC \bot (SAB))\\SB,BC \subset (SBC)\\SB \cap BC\end{array} \right. \Rightarrow HK \bot (SBC)\)
c)Do \(CK \bot (SAB)\)nên BC không thể vuông góc với (SAB)
d) Gọi M là giao điểm của SH và BC. Do \(BC \bot (SAH)\) nên \(BC \bot AM\) hay đường thẳng AM trùng với đường thẳng AK. Hay SH, AK, BC đồng quy
Đáp án C.
Cho tứ diện SABC trong đó SA, SB, SC vuông góc với nhau từng đôi một và SA = 3a, SB = a, SC = 2a. Khoảng cách từ A đến BC bằng?
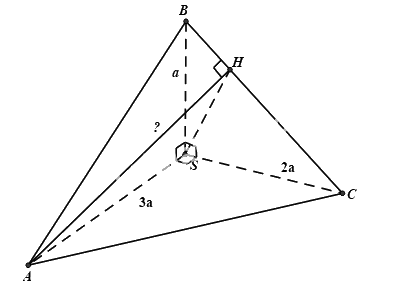
- A.
\(\frac{{3a\sqrt 2 }}{2}\).
- B.
\(\frac{{7a\sqrt 5 }}{5}\).
- C.
\(\frac{{8a\sqrt 3 }}{3}\).
- D.
\(\frac{{5a\sqrt 6 }}{6}\).
Đáp án : B
Sử dụng phương pháp tính khoảng cách từ đường thẳng tới mặt phẳng
Dựng \(AH \bot BC \Rightarrow d(A,BC) = AH\)
\(\begin{array}{l}\left\{ \begin{array}{l}SA \bot (SBC)\\AH \bot BC\end{array} \right. \Rightarrow SA \bot BC\\ \Rightarrow BC \bot (SAH) \Rightarrow BC \bot SH\end{array}\)
Xét tam giác SBC vuông tại S có SH là đường cao ta có:
\(\begin{array}{l}\frac{1}{{S{H^2}}} = \frac{1}{{S{B^2}}} + \frac{1}{{S{C^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{4{a^2}}} = \frac{5}{{4{a^2}}} \Rightarrow S{H^2} = \frac{{4{a^2}}}{5}\\ \Rightarrow SH = \frac{{2a\sqrt 5 }}{5}\end{array}\)
Ta có: \(SA \bot (SBC) \Rightarrow SA \bot SH \Rightarrow \Delta SAH\)vuông tại S
Áp dụng hệ thức lượng trong \(\Delta SAH\) vuông tại S ta có:
\(A{H^2} = S{A^2} + S{H^2} = 9{a^2} + \frac{{4{a^2}}}{5} = \frac{{49{a^2}}}{5} \Rightarrow AH = \frac{{7a\sqrt 5 }}{5}\)
Đáp án B.
Tại một cuộc hội thảo quốc tế có 50 nhà khoa học trong đó có 31 người thành thạo tiếng Anh, 21 người thành thạo tiếng Pháp và 5 người thành thạo cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một người dự hội thảo. Xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là:
- A.\(\frac{{47}}{{50}}\)
- B.\(\frac{{37}}{{50}}\)
- C.\(\frac{{39}}{{50}}\)
- D.\(\frac{{41}}{{50}}\)
Đáp án : A
Sử dụng quy tắc cộng xác suất
Gọi A là biến cố “Người được chọn thành thạo tiếng Anh”; B là biến cố “Người được chọn thành thạo tiếng Pháp”.
Biến cố: “Người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc Pháp” là biến cố hợp của A và B.
Khi đó P(A) = \(P(A) = \frac{{31}}{{50}};P(B) = \frac{{21}}{{50}};P(AB) = \frac{5}{{50}} = \frac{1}{{10}}\)
Ta có: P(A ∪ B) = P(A) + P(B) – P(AB) = \(\frac{{31}}{{50}} + \frac{{21}}{{50}} - \frac{1}{{10}} = \frac{{47}}{{50}}\)
Vậy xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là \(\frac{{47}}{{50}}\)
Đáp án A.
Cho hàm số \(y = - {x^3} + 3x - 2\) có đồ thị \(\left( C \right).\)Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung là
- A.\(y = - 2x + 1\)
- B.\(y = 2x + 1\)
- C.\(y = 3x - 2\)
- D.\(y = - 3x - 2\)
Đáp án : C
Đạo hàm của hàm số\(y = f(x)\) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm \({M_0}({x_0};f({x_0}))\)
Khi đó phương trình tiếp tuyến của (C) tại điểm M0 là: \(y = f'({x_0})(x - {x_0}) + f({x_0})\)
\(y' = \left( { - {x^3} + 3x - 2} \right)' = - 3{x^2} + 3\)
Giao điểm của \(\left( C \right)\) với trục tung là \(M(0; - 2)\)
Phương trình tiếp tuyến của \(\left( C \right)\) tại \(M(0; - 2)\) là: \(y = y'(0)(x - 0) + ( - 2) = 3x - 2\)
Đáp án C.
Cho hàm số \(y = {\sin ^2}x\). Khi đó đạo hàm y’ là
- A.\(y' = {\cos ^2}x\)
- B.\(y' = \sin 2x\)
- C.\(y' = \frac{{ - 3}}{{{{\sin }^2}x}} + 1\)
- D.\(y' = \frac{3}{{{{\sin }^2}x}}\)
Đáp án : B
Sử dụng công thức đạo hàm của hàm hợp.
\(y' = \left( {{{\sin }^2}x} \right)' = 2\sin x.c{\rm{os}}x = \sin 2x\)
Đáp án B.
Hàm số \(y = \sqrt {2 + 2{x^2}} \)có đạo hàm \(y' = \frac{{a + bx}}{{\sqrt {2 + 2{x^2}} }}\). Khi đó \(S = a - 2b\) có kết quả bằng
- A.\(S = - 4\)
- B.\(S = 10\)
- C.\(S = - 6\)
- D.\(S = 8\)
Đáp án : A
Sử dụng công thức đạo hàm của hàm hợp
\(\begin{array}{l}y' = \left( {\sqrt {2 + 2{x^2}} } \right)' = \frac{{\left( {2 + 2{x^2}} \right)'}}{{2\sqrt {2 + 2{x^2}} }} = \frac{{4x}}{{2\sqrt {2 + 2{x^2}} }} = \frac{{2x}}{{\sqrt {2 + 2{x^2}} }}\\ \Rightarrow a = 0,b = 2\\ \Rightarrow S = a - 2b = - 4\end{array}\)
Đáp án A.
Hàm số \(y = \frac{{{x^2} + x}}{{x - 1}}\)có đạo hàm \(y' = \frac{{a{x^2} + bx + c}}{{{{(x - 1)}^2}}}\). Khi đó \(S = a + b + c\) có kết quả là:
- A.1
- B.2
- C.5
- D.2
Đáp án : B
Sử dụng công thức đạo hàm của hàm hợp
\(\begin{array}{l}y' = \left( {\frac{{{x^2} + x}}{{x - 1}}} \right)' = \frac{{\left( {{x^2} + x} \right)'(x - 1) - ({x^2} + x)(x - 1)'}}{{{{(x - 1)}^2}}} = \frac{{(2x + 1)(x - 1) - ({x^2} + x)}}{{{{(x - 1)}^2}}} = \frac{{{x^2} - 2x - 1}}{{{{(x - 1)}^2}}}\\ \Rightarrow a = 1;b = - 2,c = - 1\\ \Rightarrow S = a + b + c = - 2\end{array}\)
Đáp án B.
Một chất điểm chuyển động có phương trình \(s\left( t \right) = {t^2} + 1\) (\(t\) tính bằng giây, \(s\) tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng
- A.\(1m/s.\)
- B.\(6m/s.\)
- C.\(4m/s.\)
- D.\(0m/s.\)
Đáp án : B
Phương trình vận tốc của chất điểm: \(v(t) = s'(t)\)
\(s'\left( t \right) = \left( {{t^2} + 1} \right)' = 2t\)
Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng \(v\left( 3 \right) = 2.3 = 6(m/s)\)
Đáp án B.
Hai người cùng bắn vào 1 bia. Người thứ nhất có xác suất bắn trúng là 60%, xác suất bắn trúng của người thứ 2 là 70%. Xác suất để cả hai người cùng bắn trật bằng:
- A.0,56
- B.0,21
- C.0,42
- D.0,48
Đáp án : C
Sử dụng quy tắc nhân xác suất \(P(AB) = P(A).P(B)\)
Gọi A là biến cố “người thứ nhất bắn trúng”
B là biến cố “người thứ hai bắn trúng”
AB là biến cố “cả hai người đều bắn trúng”
Suy ra \(P(A) = 0,6;P(B) = 0,7\)
Ta có: \(P(AB) = 0,6.0,7 = 0,42\)
Đáp án C.
Hàm số \(y = {x^5}\) có đạo hàm là:
- A.\(y' = 5{x^6}\)
- B.\(y' = 4{x^5}\)
- C.\(y' = 5x\)
- D.\(y' = 5{x^4}\)
Đáp án : D
Sử dụng công thức đạo hàm của hàm hợp
\(y' = \left( {{x^5}} \right)' = 5{x^4}\)
Đáp án D.
Cho mẫu số liệu về thời gian (phút) đi từ nhà đến trường của một số học sinh như sau:

a) Cỡ mẫu của mẫu số liệu = 40
b) Mốt của mẫu số liệu thuộc nhóm \(\left[ {20;25} \right)\)
c) Mốt của mẫu số liệu thuộc nhóm \(\left[ {30;35} \right)\)
d) Mốt của mẫu số liệu là \({M_0} = 22,08\)
a) Cỡ mẫu của mẫu số liệu = 40
b) Mốt của mẫu số liệu thuộc nhóm \(\left[ {20;25} \right)\)
c) Mốt của mẫu số liệu thuộc nhóm \(\left[ {30;35} \right)\)
d) Mốt của mẫu số liệu là \({M_0} = 22,08\)
Sử dụng công thức tính Mốt
Tần số lớn nhất là 12 nên nhóm chứa mốt là nhóm [20; 25). Ta có j = 2, a2 = 20, m2 = 12, m1 = 7, m3 = 5, h = 25 – 20 = 5
Khi đó
\({M_0} = {a_2} + \frac{{{m_2} - {m_1}}}{{\left( {{m_2} - {m_1}} \right) + \left( {{m_2} - {m_3}} \right)}}.5 = 20 + \frac{{12 - 7}}{{(12 - 7) + (12 - 5)}}.5 = \frac{{265}}{{12}} \approx 22,08\)
Vậy Mo ≈ 22,08.
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x + 1}}{{3x}}(C)\)
a) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Oy là: \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Ox là là\(y = - \frac{1}{3}x - \frac{1}{3}\)
c) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) tại giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là: \(y = - 3x + \frac{7}{3}\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = - \frac{1}{3}\) là \(y = - \frac{1}{3}x + 1\) và \(y = - \frac{1}{3}x - \frac{1}{3}\)
a) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Oy là: \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Ox là là\(y = - \frac{1}{3}x - \frac{1}{3}\)
c) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) tại giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là: \(y = - 3x + \frac{7}{3}\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = - \frac{1}{3}\) là \(y = - \frac{1}{3}x + 1\) và \(y = - \frac{1}{3}x - \frac{1}{3}\)
Bước 1: Gọi M(x0; f(x0)) là tọa độ tiếp điểm của tiếp tuyến của (C) thì f'(x0) = k
Bước 2: Giải phương trình f'(x0) = k với ẩn là x0.
Bước 3:Phương trình tiếp tuyến của (C) có dạng y = k(x – x0) + f(x0).
\(y' = f'(x) = \left( {\frac{{x + 1}}{{3x}}} \right)' = \frac{{ - 1}}{{3{x^2}}}\)
Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm của cạnh BC. AH, IJ là đường cao tam giác AID.
a) \(BC \bot (AID)\)
b) \(AH \bot (BCD)\)
c) IJ là đường vuông góc chung của AD và BC
d) H là trọng tâm tam giác BCD
a) \(BC \bot (AID)\)
b) \(AH \bot (BCD)\)
c) IJ là đường vuông góc chung của AD và BC
d) H là trọng tâm tam giác BCD
Sử dụng định lý đường thẳng vuông góc với mặt phẳng
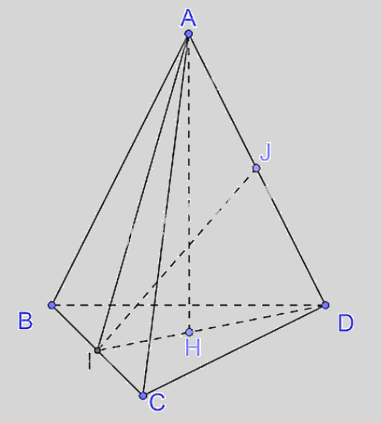
a) Vì tam giác ABC cân tại A, AI là trung tuyến nên AI đồng thời là đường cao hay AI \( \bot \)
Vì tam giác BCD cân tại D, DI là trung tuyến nên DI đồng thời là đường cao hay DI \( \bot \) BC.
Có AI \( \bot \)BC và DI \( \bot \) BC nên BC \( \bot \) (AID).
b) Do AH là đường cao của tam giác AID nên AH \( \bot \)
Vì BC \( \bot \) (AID) nên BC \( \bot \) AH mà AH\( \bot \)DI nên AH \( \bot \) (BCD).
c) Vì BC \( \bot \)(AID) nên BC \( \bot \)IJ, mà IJ là đường cao của tam giác AID nên IJ \( \bot \) Do đó IJ là đường vuông góc chung của AD và BC.
d) Tam giác BCD cân nên H không là trọng tâm tam giác BCD
Trong đợt kiểm tra cuối học kì II lớp 11 của các trường trung học phổ thông, thống kê cho thấy có 93% học sinh tỉnh X đạt yêu cầu; 87% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y. Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập
a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là\(0,7809\)
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là \(0,0091\)
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là \(0,1818\)
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là \(0,9909\)
a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là\(0,7809\)
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là \(0,0091\)
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là \(0,1818\)
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là \(0,9909\)
Sử dụng công thức nhân xác suất cho hai biến cố độc lập
Xác suất để học sinh tỉnh X không đạt yêu cầu là \(100\% - 93\% = 7\% = 0,07\)
Xác suất để học sinh tỉnh Y không đạt yêu cầu là \(100\% - 87\% = 13\% = 0,13\)
Gọi A là biến cố: “Học sinh tỉnh X đạt yêu cầu”
B là biến cố: “Học sinh tỉnh Y đạt yêu cầu”
Khi đó ta có: \(P(A) = 0,93;P(B) = 0,87;P(\overline A ) = 0,07;P(\overline B ) = 0,13\)
a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là:
\(P(AB) = P(A).P(B) = 0,93.0,87 = 0,8091\)
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là
\(P(\overline {AB} ) = P(\overline A ).P(\overline B ) = 0,07.0,13 = 0,0091\)
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là:
\(P(A\overline B ) + P(\overline A B) = 0,93.0,13 + 0,07.0,87 = 0,1818\)
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là:
\(P(A \cup B) = P(A) + P(B) - P(AB) = 0,93 + 0,87 - 0,8091 = 0,9909\)
Tính giới hạn: \(I = \mathop {lim}\limits_{x \to - 3} \frac{{{x^2} + 2x - 3}}{{{x^2} + 5x + 6}}\)
Sử dụng phương pháp phân tích thành nhân tử
\(I = \mathop {lim}\limits_{x \to - 3} \frac{{{x^2} + 2x - 3}}{{{x^2} + 5x + 6}} = \mathop {lim}\limits_{x \to - 3} \frac{{(x + 3)(x - 1)}}{{(x + 3)(x + 2)}}\)
\( = \mathop {lim}\limits_{x \to - 3} \frac{{x - 1}}{{x + 2}} = 4\)
Cho hàm số : \(y = 5{x^4} - 3{x^3} + 6x - \sqrt 7 \). Tính \(f'\left( 0 \right)\).
Sử dụng công thức tính đạo hàm của hàm hợp
\(\begin{array}{l}y' = 20{x^3} - 9{x^2} + 6\\y'(0) = 6\end{array}\)
Cho hình chóp tứ giác đều\(S.ABCD\)có tất cả các cạnh bằng \(a\). Tính khoảng cách từ đỉnh \(S\) đến mặt phẳng \((ABCD).\)
\(d(S,(ABCD)) = SO\)
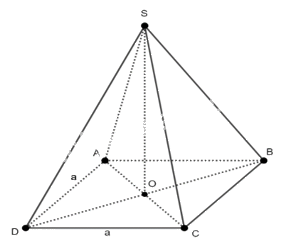
Gọi \(O\) là tâm của hình vuông \(ABCD.\) Suy ra \(SO \bot (ABCD)\) hay \(SO \bot BD\)
Xét hình vuông \(ABCD\) cạnh \(a,\) ta có \(AD = AB = a.\)
Suy ra \(BD = a\sqrt 2 \)(đường chéo hình vuông)\( \Rightarrow OD = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác vuông \(SDO\)vuông tại \(O,\) áp dụng định lý Pitago ta có: \(S{D^2} = S{O^2} + O{D^2} \Rightarrow S{O^2} = S{D^2} - O{D^2} = {a^2} - {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = \frac{{{a^2}}}{2} \Rightarrow SO = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d(S,(ABCD)) = SO = \frac{{a\sqrt 2 }}{2}.\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\).Cạnh bên \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\sqrt 2 \).Góc giữa đường thẳng \(SC\)và mặt phẳng \(\left( {ABCD} \right)\)bằng
Sử dụng phương pháp xác định góc giữa đường thẳng và mặt phẳng
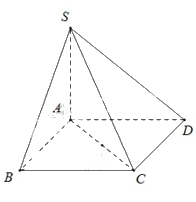
\(\left( {\widehat {SC,\left( {ABCD} \right)}} \right) = \left( {\widehat {SC,AC}} \right) = \widehat {SCA}\)
Tam giác \(SAC\) có \(SA \bot AC,SA = AC = a\sqrt 2 \) Suy ra \(\widehat {SCA} = {45^0}.\)
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) với \(a,b,c \in \mathbb{R}\). Biết rằng đồ thị hàm số đi qua hai điểm \(A\left( {1; - 3} \right)\) và \(B\left( {2;3} \right)\), đồng thời tiếp tuyến của đồ thị tại điểm có hoành độ bằng \( - 1\) có hệ số góc bằng 2. Tính tổng \(S = a + b + c\).
Viết phương trình hàm số biết đồ thị hàm số đi qua A và B; đồng thời là tiếp tuyến có hoành độ bằng -1 có hệ số góc bằng 2.
Từ đó lập hệ phương trình 3 ẩn tương ứng
Đồ thị hàm số đi qua điểm \(A\left( {1; - 3} \right)\) nên \( - 3 = a + b + c\) \(\left( 1 \right)\)
Đồ thị hàm số đi qua điểm \(B\left( {2;3} \right)\) nên \(16a + 4b + c = 3\) \(\left( 2 \right)\)
Tiếp tuyến của đồ thị tại điểm có hoành độ bằng \( - 1\) có hệ số góc bằng 2 nên \(f'\left( { - 1} \right) = 2 \Leftrightarrow - 4a - 2b = - 2 \Leftrightarrow 2a + b = 1\) \(\left( 3 \right)\)
Từ \(\left( 1 \right)\), \(\left( 2 \right)\), \(\left( 3 \right)\) ta có hệ phương trình:
\(\left\{ \begin{array}{l}a + b + c = - 3\\16a + 4b + c = 3\\2a + b = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 3\\c = - 1\end{array} \right.\)
Vậy \(S = -3\).
Cho hàm số \(y = \frac{{x - 2}}{{x + 3}}\) có đồ thị \(\left( C \right).\) Tìm điểm \(M\) trên đồ thị \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)tạo với hai trục tọa độ một tam giác có diện tích bằng \(\frac{{18}}{5}.\)
Gọi tọa độ điểm M thuộc \(\left( C \right)\). Lập phương trình tính diện tích tam giác
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\)
Gọi \(M\left( {a;\frac{{a - 2}}{{a + 3}}} \right) \in \left( C \right)\).
\(y' = \frac{5}{{{{\left( {x + 3} \right)}^2}}}\)
Phương trình tiếp tuyến của \(\left( C \right)\) tại \(M\): \(y = \frac{5}{{{{\left( {a + 3} \right)}^2}}}\left( {x - a} \right) + \frac{{a - 2}}{{a + 3}}{\rm{ }}\left( \Delta \right)\)
\(A = Ox \cap \Delta \Rightarrow A\left( {\frac{{ - {a^2} + 4a + 6}}{5};0} \right)\)
\(B = Oy \cap \Delta \Rightarrow B\left( {0;\frac{{{a^2} - 4a - 6}}{{{{\left( {a + 3} \right)}^2}}}} \right)\)
\(\begin{array}{l}{S_{OAB}} = \frac{1}{2}OA.OB \Leftrightarrow \frac{1}{2}\left| {\frac{{ - {a^2} + 4a + 6}}{5}} \right|.\left| {\frac{{{a^2} - 4a - 6}}{{{{\left( {a + 3} \right)}^2}}}} \right| = \frac{{18}}{5}\\ \Leftrightarrow {\left( {{a^2} - 4a - 6} \right)^2} = 36{\left( {a + 3} \right)^2}\\ \Leftrightarrow \left[ \begin{array}{l}{a^2} - 10a - 24 = 0\\{a^2} + 2a + 12 = 0:vn\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 12\\a = - 2\end{array} \right.\end{array}\)
Vậy \(M\left( {12;\frac{2}{3}} \right)\) hoặc \(M\left( { - 2; - 4} \right).\)
Đề thi học kì 2 Toán 11 Cánh diều - Đề số 4: Tổng quan và Hướng dẫn Ôn tập
Học kì 2 Toán 11 là giai đoạn quan trọng để học sinh củng cố kiến thức nền tảng và chuẩn bị cho các kỳ thi quan trọng. Đề thi học kì 2 Toán 11 Cánh diều - Đề số 4 đóng vai trò là công cụ hỗ trợ đắc lực cho quá trình ôn tập này. Bài viết này sẽ cung cấp thông tin chi tiết về đề thi, cấu trúc, nội dung và hướng dẫn ôn tập hiệu quả.
Cấu trúc Đề thi học kì 2 Toán 11 Cánh diều - Đề số 4
Đề thi thường bao gồm các phần chính sau:
- Phần trắc nghiệm: Kiểm tra kiến thức cơ bản và khả năng vận dụng nhanh các công thức, định lý.
- Phần tự luận: Đòi hỏi học sinh trình bày chi tiết lời giải, áp dụng kiến thức vào giải quyết các bài toán phức tạp.
Tỷ lệ phân bổ điểm giữa hai phần có thể khác nhau tùy theo quy định của từng trường, nhưng thường phần tự luận chiếm tỷ trọng cao hơn.
Nội dung Đề thi học kì 2 Toán 11 Cánh diều - Đề số 4
Nội dung đề thi bao gồm các chủ đề chính sau:
- Hàm số lượng giác: Khảo sát hàm số, phương trình lượng giác, bất phương trình lượng giác.
- Đạo hàm: Khái niệm đạo hàm, các quy tắc tính đạo hàm, ứng dụng đạo hàm trong việc khảo sát hàm số.
- Giới hạn: Khái niệm giới hạn, các tính chất của giới hạn, tính giới hạn của hàm số.
- Hình học giải tích: Đường thẳng, đường tròn, elip, hypebol, parabol.
- Phép biến hình: Phép tịnh tiến, phép quay, phép dời hình, phép đồng dạng.
Hướng dẫn Ôn tập hiệu quả cho Đề thi học kì 2 Toán 11 Cánh diều - Đề số 4
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các công thức, định lý và ví dụ minh họa.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau, từ dễ đến khó, để rèn luyện kỹ năng giải quyết vấn đề.
- Sử dụng các tài liệu ôn tập: Tham khảo các đề thi tham khảo, đề thi năm trước và các tài liệu ôn tập khác để làm quen với cấu trúc và nội dung đề thi.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, hãy hỏi thầy cô giáo, bạn bè hoặc tham gia các diễn đàn, nhóm học tập trực tuyến.
- Lập kế hoạch ôn tập: Chia nhỏ nội dung ôn tập thành các phần nhỏ hơn và lập kế hoạch ôn tập cụ thể để đảm bảo ôn tập đầy đủ và hiệu quả.
Tầm quan trọng của việc giải Đề thi học kì 2 Toán 11 Cánh diều - Đề số 4
Việc giải đề thi này không chỉ giúp học sinh làm quen với cấu trúc đề thi mà còn giúp học sinh đánh giá được trình độ hiện tại của mình và xác định những kiến thức còn yếu để tập trung ôn tập. Đồng thời, việc giải đề thi còn giúp học sinh rèn luyện kỹ năng làm bài thi, quản lý thời gian và giảm bớt áp lực tâm lý khi bước vào phòng thi.
Tusach.vn – Nguồn tài liệu ôn thi Toán 11 uy tín
Tusach.vn tự hào là một trong những nguồn cung cấp tài liệu ôn thi Toán 11 uy tín và chất lượng. Chúng tôi cung cấp đầy đủ các loại tài liệu ôn tập, bao gồm đề thi, bài tập, đáp án, video bài giảng và các tài liệu tham khảo khác. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác và chuẩn bị tốt nhất cho kỳ thi học kì 2 Toán 11!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Hàm số lượng giác | Cao |
| Đạo hàm | Cao |
| Giới hạn | Trung bình |
| Hình học giải tích | Trung bình |
| Nguồn: Tusach.vn | |