Đề thi học kì 2 Toán 11 Cánh diều - Đề số 2
Tổng quan nội dung
Đề thi học kì 2 Toán 11 Cánh diều - Đề số 2
Tusach.vn xin giới thiệu Đề thi học kì 2 Toán 11 Cánh diều - Đề số 2, một tài liệu ôn tập quan trọng dành cho học sinh lớp 11. Đề thi được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo.
Đề thi này không chỉ giúp các em làm quen với dạng đề mà còn rèn luyện kỹ năng giải quyết bài toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Đề bài
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\)có nghiệm là
- A.
\(x = - 1\)
- B.
\(x = 1,\,\,x = 4\)
- C.
\(x = - 1,\,\,x = 4\)
- D.
\(x = 0,\,\,x = 3\)
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm\(M( - 2;6).\) Phương trình của (d) là
- A.y = -11x +30.
- B.y = 13x + 34.
- C.y = -11x – 16.
- D.y = 13x – 18.
Tính thời gian trung bình giải bài tập của học sinh lớp 11A được cho trong bảng sau:

- A.17
- B.15
- C.13,4
- D.14,3
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
- A.
\({\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^{}}}}\)
- B.
\({\left( {k.u} \right)^\prime } = k.u'\)
- C.
\({\left( {u + v} \right)^\prime } = u' + v'\)
- D.
\(\left( {u.v} \right)' = u'.v + u.v'\)
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\)là
- A.
\(y' = \frac{3}{{{{\left( { - x + 1} \right)}^2}}}\)
- B.
\(y' = \frac{1}{{{{\left( {x - 1} \right)}^2}}}\)
- C.
\(y' = \frac{{ - 1}}{{{{\left( {1 - x} \right)}^2}}}\)
- D.
\(y' = \frac{{ - 3}}{{{{\left( {1 - x} \right)}^2}}}\)
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm x0 = 1 thì m bằng:
- A.-1
- B.1
- C.2
- D.0
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
- A.
\(y' = 4{x^3} - 3x + 2\)
- B.
\(y' = 4{x^4} - 6x + 2\)
- C.
\(y' = 4{x^3} - 6x + 3\)
- D.
\(y' = 4{x^3} - 6x + 2\)
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
- A.
\( - \frac{1}{2}\)
- B.
\( + \infty \)
- C.
\(\frac{a}{3}\)
- D.
\( - \infty \)
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
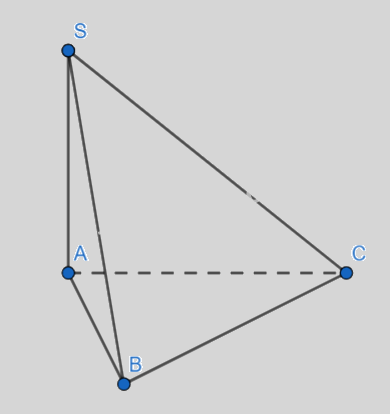
- A.
\(90^\circ .\)
- B.
\(60^\circ .\)
- C.
\(45^\circ .\)
- D.
\(30^\circ .\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
- A.
\((SDC) \bot (SAC)\)
- B.
\((SCD) \bot (SAD)\)
- C.
\((SBD) \bot (SAC)\)
- D.
\((SBC) \bot (SAC)\)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
- A.
\(AC \bot (SBD)\)
- B.
\(AB \bot (SAD)\)
- C.
\(AC \bot (SBD)\)
- D.
\(SO \bot (ABCD)\)
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\)bằng
- A.232.
- B.72.
- C.152.
- D.-75.
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
Cho mẫu số liệu về cân nặng (kg) của 45 học sinh lớp 11A được cho bởi bảng sau:

a) Tứ phân vị thứ nhất \({Q_1}\) là 47
b) Trung vị \({M_e}\) là 51,4
c) Tứ phân vị thứ ba \({Q_3}\) là 54,2
d) Mốt \({M_o} = 20\)
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) \(d((MNP),(ABC)) = h\)
b) \(d(NP,(ABC)) = \frac{h}{2}\)
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d) \((MNP)//(ABC)\)
Cho hàm số \(y = \sin x\)
a) Đạo hàm của hàm số là \(y' = - cosx\)
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Tính giới hạn: \(\mathop {lim}\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}}\).
Cho hàm số: \(y = {\left( {{x^4} - 1} \right)^4}\). Tính \(y'(1)\)
Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{x - 1}}\,\,\,\;khi\,\,x \ne 1\\1 - mx\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\)liên tục tại điểm\({x_0} = 1\)
Cho hình chóp S.ABCD đáy là hình vuông cạnh a , cạnh bên SA \( \bot \)(ABCD) và
SA = a\(\sqrt 2 \). Tính tan của góc giữa hai mp (SBC) và (ABCD).
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\). Tìm tọa độ điểm M thuộc đồ thị sao cho khoảng cách từ điểm \(I( - 1;2)\)tới tiếp tuyến của đồ thị tại M là lớn nhất.
Với mức tiêu thụ thức ăn cho cá hàng ngày của hộ gia đình A không đổi như dự định thì lượng thức ăn dự trữ sẽ hết sau 50 ngày. Nhưng trên thực tế, mức tiêu thụ thức ăn tăng thêm 3% từ ngày đầu tiên và cứ tiếp tục như vậy, ngày sau tăng thêm 3% so với ngày kề trước đó. Hỏi thực tế, lượng thức ăn dự trữ đó sẽ hết sau bao nhiêu ngày? (làm tròn đến hàng đơn vị).
Lời giải và đáp án
Cho hàm số \(f(x) = \frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6.\) Phương trình \(f'(x) = 0\)có nghiệm là
- A.
\(x = - 1\)
- B.
\(x = 1,\,\,x = 4\)
- C.
\(x = - 1,\,\,x = 4\)
- D.
\(x = 0,\,\,x = 3\)
Đáp án : C
Sử dụng công thức đạo hàm.
\(\begin{array}{l}f'(x) = \left( {\frac{{{x^3}}}{3} - \frac{3}{2}{x^2} - 4x + 6} \right)' = 3{x^2} - 3x - 4 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 4\end{array} \right.\end{array}\)
Đáp án C.
Gọi (d) là tiếp tuyến của đồ thị hàm số\(y = f(x) = - {x^3} + x\) tại điểm\(M( - 2;6).\) Phương trình của (d) là
- A.y = -11x +30.
- B.y = 13x + 34.
- C.y = -11x – 16.
- D.y = 13x – 18.
Đáp án : C
Phương trình tiếp tuyến với đồ thị (C): \(y = f(x) = - {x^3} + x\) tại điểm \(M({x_0};f({x_0})).\)là:
\(y = f'(x{}_0)(x - x{}_0) + f(x{}_0)\)
Trong đó:
\(M({x_0};f({x_0}))\) gọi là tiếp điểm.
\(k = f'(x{}_0)\)là hệ số góc.
\(y' = f'(x) = \left( { - {x^3} + x} \right)' = - 3{x^2} + 1\)
Phương trình tiếp tuyến của đồ thị \(y = f(x) = - {x^3} + x\)tại điểm \(M({x_0};f({x_0})).\)
\(y' = f'( - 2)(x + 2) + 6 = - 11(x + 2) + 6 = - 11x - 16\)
Đáp án C.
Tính thời gian trung bình giải bài tập của học sinh lớp 11A được cho trong bảng sau:

- A.17
- B.15
- C.13,4
- D.14,3
Đáp án : C
Sử dụng công thức tính số trung bình của mẫu số liệu
Trong mỗi khoảng thời gian, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có bảng sau:

Tổng số học sinh là n = 45. Thời gian trung bình giải bài toán của học sinh lớp 11 A là:
\(\overline x = \frac{{6.9 + 17.12 + 17.15 + 5.18}}{{45}} = \frac{{67}}{5} = 13,4\) (phút)
Đáp án C.
Cho \(u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\); với k là hằng số. Hãy chọn khẳng định sai?
- A.
\({\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^{}}}}\)
- B.
\({\left( {k.u} \right)^\prime } = k.u'\)
- C.
\({\left( {u + v} \right)^\prime } = u' + v'\)
- D.
\(\left( {u.v} \right)' = u'.v + u.v'\)
Đáp án : A
Áp dụng công thức tính đạo hàm.
Ta có:
\({\left( {\frac{1}{v}} \right)^\prime } = - \frac{{v'}}{{{v^2}}}\).
\({\left( {k.u} \right)^\prime } = k.u'\).
\({\left( {u + v} \right)^\prime } = u' + v'\).
\(\left( {u.v} \right)' = u'.v + u.v'\).
Vậy đáp án A sai.
Đạo hàm của hàm số \(y = \frac{{2x - 1}}{{1 - x}}\)là
- A.
\(y' = \frac{3}{{{{\left( { - x + 1} \right)}^2}}}\)
- B.
\(y' = \frac{1}{{{{\left( {x - 1} \right)}^2}}}\)
- C.
\(y' = \frac{{ - 1}}{{{{\left( {1 - x} \right)}^2}}}\)
- D.
\(y' = \frac{{ - 3}}{{{{\left( {1 - x} \right)}^2}}}\)
Đáp án : B
Sử dụng công thức tính đạo hàm của hàm phân thức: \(y' = \left( {\frac{{ax + b}}{{cx + d}}} \right)' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\)
\(y' = \left( {\frac{{2x - 1}}{{1 - x}}} \right)' = \left( {\frac{{2x - 1}}{{ - x + 1}}} \right)' = \frac{1}{{{{\left( { - x + 1} \right)}^2}}}\)
Đáp án B.
Cho hàm số: \(f(x) = \left\{ \begin{array}{l}\frac{{{x^2} - 1}}{{x - 1}}\quad khi\;x \ne 1\\m\quad \quad \quad khi\;x = 1\end{array} \right.\) . Để f(x) liên tục tại điểm x0 = 1 thì m bằng:
- A.-1
- B.1
- C.2
- D.0
Đáp án : C
Điều kiện để hàm số liên tục tại \(x = {x_0}\):
\(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\)
Hàm số đã cho xác định trên R
Ta có:
\(\begin{array}{l}f(1) = m\\\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{1}{{x + 1}} = \frac{1}{2}\end{array}\)
Hàm số liên tục tại \(x = 1\) khi \(f(1) = \mathop {\lim }\limits_{x \to 1} f(x) \Leftrightarrow m = \frac{1}{2}\)
Vậy khi m = 2 thì hàm số liên tục tại \(x = 1\)
Đáp án C.
Tìm đạo hàm của hàm số sau \(y = {x^4} - 3{x^2} + 2x - 1\)
- A.
\(y' = 4{x^3} - 3x + 2\)
- B.
\(y' = 4{x^4} - 6x + 2\)
- C.
\(y' = 4{x^3} - 6x + 3\)
- D.
\(y' = 4{x^3} - 6x + 2\)
Đáp án : D
Sử dụng công thức tính đạo hàm của hàm hợp
\(y' = 4{x^3} - 6x + 2\)
Đáp án D.
Cho hàm số \(f(x) = \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}},(a \in R,a \ne 0)\). Khi đó \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) bằng
- A.
\( - \frac{1}{2}\)
- B.
\( + \infty \)
- C.
\(\frac{a}{3}\)
- D.
\( - \infty \)
Đáp án : A
Nhận dạng: \(\mathop {\lim }\limits_{x \to \infty } \frac{{f(x)}}{{g(x)}}\)
TH1: Nếu f(x) , g(x) là các đa thức thì chia cả tử và mẫu cho lũy thừa cao nhất của x.
TH2: Nếu f(x) , g(x) chứa căn thì có thể chia cả tử và mẫu cho lũy thừa cao nhất của x hoặc nhân lượng liên hợp
\(\mathop {\lim }\limits_{x \to \infty } f(x) = \mathop {\lim }\limits_{x \to \infty } \frac{{a{x^2} + 4x + 3}}{{3x - 2a{x^2}}} = \mathop {\lim }\limits_{x \to \infty } \frac{{{x^2}(a + \frac{4}{x} + \frac{3}{{{x^2}}})}}{{{x^2}( - 2a + \frac{3}{x})}} = \frac{a}{{ - 2a}} = \frac{{ - 1}}{2}\)
Đáp án A.
Cho hình chóp \(S.ABC\) có đáy ABC là tam giác vuông tại B và SA vuông góc mặt đáy \(\left( {ABC} \right)\), \(SB = 2a\), \(AB = a\)( tham khảo hình vẽ). Tính góc giữa SB và \(mp\left( {ABC} \right)\)
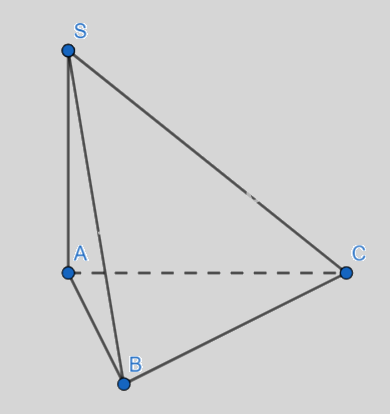
- A.
\(90^\circ .\)
- B.
\(60^\circ .\)
- C.
\(45^\circ .\)
- D.
\(30^\circ .\)
Đáp án : B
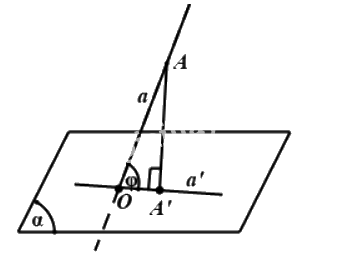
Bước 1: Tìm giao điểm O của đường thẳng a và \((\alpha )\)
Bước 2: Xác định hình chiếu A’ của điểm A xuống \((\alpha )\)
Bước 3: Suy ra: \(\left( {AO,(\alpha )} \right) = \left( {AO,A'O} \right) = \widehat {AOA'}\)
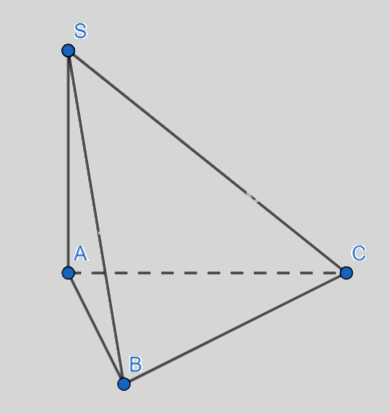
Do \(SA \bot (ABC)\)nên A là hình chiếu của S lên (ABC)
Ta có: \(\left( {SB,(ABC)} \right) = (SB,AB)\)
Xét \(\Delta SAB\) vuông tại A có:
\(\begin{array}{l}\tan \left( {SB,AB} \right) = \tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{\sqrt {S{B^2} - A{B^2}} }}{{AB}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3 \\ \Rightarrow \widehat {SBA} = {60^0}\end{array}\)
Đáp án B.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng?
- A.
\((SDC) \bot (SAC)\)
- B.
\((SCD) \bot (SAD)\)
- C.
\((SBD) \bot (SAC)\)
- D.
\((SBC) \bot (SAC)\)
Đáp án : B
Sử dụng định lý đường thẳng vuông góc với mặt phẳng và hai mặt phẳng vuông góc với nhau
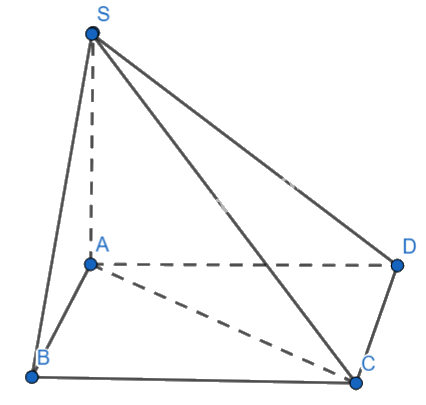
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\\SA,AD \subset (SAD)\\SA \cap AD\end{array} \right. \Rightarrow CD \bot (SAD)\\CD \subset (SCD) \Rightarrow (SCD) \bot (SAD)\end{array}\)
Đáp án B.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC, SB = SD. Khẳng định nào sau đây đúng ?
- A.
\(AC \bot (SBD)\)
- B.
\(AB \bot (SAD)\)
- C.
\(AC \bot (SBD)\)
- D.
\(SO \bot (ABCD)\)
Đáp án : C
Sử dụng định lý đường thẳng vuông góc với mặt phẳng
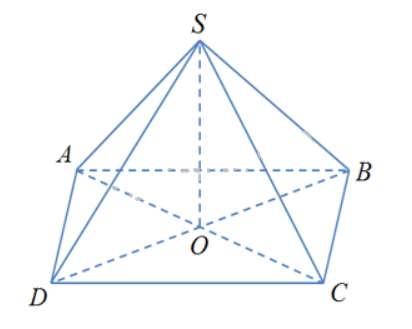
Ta có:
\(\left\{ \begin{array}{l}AC \bot BD\\AC \bot SO\\BD,SO \subset (SBD)\\BD \cap SO\end{array} \right. \Rightarrow AC \bot (SBD)\)
Đáp án C.
Với hàm số \(g\left( x \right) = \frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}};\,g'\left( 2 \right)\)bằng
- A.232.
- B.72.
- C.152.
- D.-75.
Đáp án : B
Sử dụng phương tính đạo hàm của hàm hợp
\(\begin{array}{l}g'\left( x \right) = \left[ {\frac{{\left( {2x + 1} \right){{\left( {2 - 3x} \right)}^2}}}{{x - 1}}} \right]' = \left( {\frac{{18{x^3} - 15{x^2} - 4x + 4}}{{x - 1}}} \right)'\\ = \frac{{\left( {18{x^3} - 15{x^2} - 4x + 4} \right)'(x - 1) - (18{x^3} - 15{x^2} - 4x + 4)(x - 1)'}}{{{{\left( {x - 1} \right)}^2}}}\\ = \frac{{36{x^3} - 69{x^2} + 30x}}{{{{\left( {x - 1} \right)}^2}}}\\g'\left( 2 \right) = 72\end{array}\)
Đáp án B.
Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
a) Xác suất để 3 viên bi lấy ra đều màu đỏ là \(\frac{{14}}{{285}}\)
b) Xác suất để 3 viên bi lấy ra có không quá hai màu là \(\frac{{43}}{{57}}\)
c) Xác suất để 3 viên bi lấy ra đều có màu vàng là \(\frac{1}{7}\)
d) Xác suất để 3 viên bi lấy ra có đủ cả ba màu là \(\frac{{14}}{{57}}\)
Sử dụng các quy tắc đếm để xác định số phần tử của không gian mẫu và biến cố
Không gian mẫu: \((\Omega ) = C_{20}^3 = 1140\)
a) Gọi A là biến cố: “3 viên bi lấy ra đều màu đỏ”; \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{C_8^3}}{{C_{20}^3}} = \frac{{56}}{{1140}} = \frac{{14}}{{285}}\)
b) B là biến cố: “3 viên bi lấy ra có không quá hai màu”
TH1: Số cách lấy ra 3 viên bi lấy ra chỉ có một màu: \(C_8^3 + C_7^3 + C_5^3 = 101\)
TH2: Số cách lấy ra 3 viên bi lấy ra chỉ có đúng hai màu: \(\left[ {C_{15}^3 - \left( {C_8^3 + C_7^3} \right)} \right] + \left[ {C_{13}^3 - \left( {C_8^3 + C_5^3} \right)} \right] + \left[ {C_{12}^3 - \left( {C_5^3 + C_7^3} \right)} \right] = 759\)
Nên: \(P(B) = \frac{{n(B)}}{{n(\Omega )}} = \frac{{101 + 759}}{{1140}} = \frac{{43}}{{57}}\)
c) C là biến cố: “3 viên bi lấy ra đều có màu vàng”; \(P(C) = \frac{{n(C)}}{{n(\Omega )}} = \frac{{C_5^3}}{{C_{20}^3}} = \frac{{10}}{{1140}} = \frac{1}{{114}}\)
d) D là biến cố: “3 viên bi lấy ra có đủ cả ba màu”: \(P(D) = \frac{{n(D)}}{{n(\Omega )}} = \frac{{C_8^1.C_7^1.C_5^1}}{{C_{20}^3}} = \frac{{280}}{{1140}} = \frac{{14}}{{57}}\)
Cho mẫu số liệu về cân nặng (kg) của 45 học sinh lớp 11A được cho bởi bảng sau:

a) Tứ phân vị thứ nhất \({Q_1}\) là 47
b) Trung vị \({M_e}\) là 51,4
c) Tứ phân vị thứ ba \({Q_3}\) là 54,2
d) Mốt \({M_o} = 20\)
a) Tứ phân vị thứ nhất \({Q_1}\) là 47
b) Trung vị \({M_e}\) là 51,4
c) Tứ phân vị thứ ba \({Q_3}\) là 54,2
d) Mốt \({M_o} = 20\)
Sử dụng công thức tính tứ phân vị của mẫu số liệu và Mốt
Cỡ mẫu là n = 7 + 10 + 20 + 6 + 2 = 45
Gọi x1, x2, ….., x45 là cân nặng của 45 học sinh và giả sử dãy này đã được sắp xếp theo thứ tự tăng dần.
Khi đó, trung vị là x23. Do giá trị x23 thuộc nhóm [50; 55) nên nhóm này chứa trung vị.
Do đó p = 3; a3 = 50, m3 = 20; m1 + m2 = 7 + 10 = 17; a4 – a3 = 55 – 50 = 5
Khi đó
\({M_e} = {a_3} + \frac{{\frac{n}{2} - ({m_1} + {m_2})}}{{{m_3}}}({a_4} - {a_3}) = 50 + \frac{{\frac{{45}}{2} - 17}}{{20}}.5 \approx 51,4\).
Vậy Me = 51,4.
Từ Me = 51,4, suy ra Q2 = 51,4.
- Tứ phân vị thứ nhất Q1 là trung vị của nửa dãy bên trái Q2 nên \({Q_1} = \frac{{{x_{11}} + {x_{12}}}}{2}\)
Do x11 và x12 đều thuộc nhóm [45; 50) nên nhóm này chứa Q1. Do đó, p = 2, a2 = 45, m2 = 10, m1 = 7; a3 – a2 = 5.
Ta có \({Q_1} = {a_2} + \frac{{\frac{n}{4} - {m_1}}}{{{m_2}}}({a_3} - {a_2}) = 45 + \frac{{\frac{{45}}{2} - 7}}{{10}}.5 \approx 47,1\)
- Tứ phân vị thứ ba Q3 là trung vị của nửa dãy bên phải Q2 nên \({Q_3} = \frac{{{x_{34}} + {x_{35}}}}{2}\).
Do x34 và x35 đều thuộc nhóm [50; 55) nên nhóm này chứa Q3. Do đó, p = 3, a3 = 50, m3 = 20, m1 + m2 = 7 + 10 = 17; a4 – a3 = 55 – 50 = 5.
Ta có \({Q_3} = {a_3} + \frac{{\frac{{3n}}{4} - ({m_1} + {m_2})}}{{{m_3}}}({a_4} - {a_3}) = 50 + \frac{{\frac{{3.45}}{4} - 17}}{{20}}.5 \approx 54,2\) .
Vậy tứ phân vị: Q1 ≈ 47,1; Q2 ≈ 51,4; Q3 ≈ 54,2.
- Ta thấy tần số lớn nhất là 20 nên nhóm chứa mốt là nhóm [50; 55).
Ta có j = 3, a3 = 50, m3 = 20, m2 = 10, m4 = 6, h = 55 – 50 = 5
Khi đó
\({M_0} = {a_3} + \frac{{{m_3} - {m_2}}}{{\left( {{m_3} - {m_2}} \right) + \left( {{m_3} - {m_4}} \right)}}h = 50 + \frac{{20 - 10}}{{(20 - 10) + (20 - 6)}}.5 \approx 52,1\)
Vậy Mo ≈ 52,1.
Cho hình chóp S.ABC có SA ⊥ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) \(d((MNP),(ABC)) = h\)
b) \(d(NP,(ABC)) = \frac{h}{2}\)
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d) \((MNP)//(ABC)\)
a) \(d((MNP),(ABC)) = h\)
b) \(d(NP,(ABC)) = \frac{h}{2}\)
c) \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d) \((MNP)//(ABC)\)
Sử dụng phương pháp tính khoảng cách từ điểm đến mặt phẳng và khoảng cách từ đường thẳng đến mặt phẳng
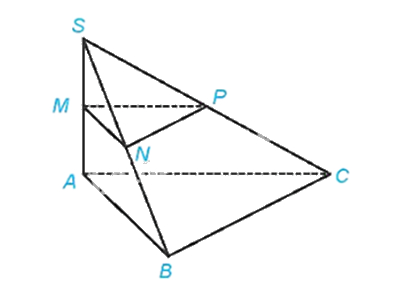
a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB nên MN là đường trung bình của tam giác SAB. Suy ra \(MN//AB\),do đó \(MN//(ABC)\)
Xét tam giác SBC có N là trung điểm của SB, P là trung điểm của SC nên PN là đường trung bình của tam giác SBC. Suy ra \(PN//BC\),do đó \(PN//(ABC)\)
Khi đó, \(d((MNP),(ABC)) = d(M,(ABC))\)
Vì \(SA \bot (ABC)\) nên \(MA \bot (ABC)\). Do đó \(d(M,(ABC)) = MA\)
Vì M là trung điểm SA nên \(AM = \frac{{SA}}{2} = \frac{h}{2}\)
Do đó \(d((MNP),(ABC)) = \frac{h}{2}\)
b) Vì \(PN//(ABC)\) nên \(d(NP,(ABC)) = d(N,(ABC))\)
Vì \(MN//(ABC)\) nên \(d(N,(ABC)) = d(M,(ABC)) = MA = \frac{h}{2}\)
Vậy \(d(N,(ABC)) = \frac{h}{2}\)
c) Vì tam giác ABC là tam giác vuông tại B nên \(BC \bot AB\)
Vì \(SA \bot (ABC)\) nên \(SA \bot BC\)mà \(BC \bot AB\) nên \(BC \bot (SAB)\), suy ra \((SBC) \bot (SAB)\)
Kẻ \(AH \bot SB\) tại H
Vì \(\left\{ \begin{array}{l}(SBC) \bot (SAB)\\(SBC) \cap (SAB) = SB\\AH \subset (SAB)\\AH \bot SB\end{array} \right. \Rightarrow AH \bot (SBC)\)
Khi đó \(d(A,(SBC)) = AH\)\(\)
Vì \(SA \bot (SBC)\) nên \(SA \bot AB\)
Xét tam giác SAB vuông tại A, AH là đường cao, có:
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{a^2}{h^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Vậy \(d(A,(SBC)) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
d)\(MN//(ABC)\) mà \(MN \subset (MNP) \Rightarrow (MNP)//(ABC)\)
Cho hàm số \(y = \sin x\)
a) Đạo hàm của hàm số là \(y' = - cosx\)
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
a) Đạo hàm của hàm số là \(y' = - cosx\)
b) Biểu thức \(y'(\frac{\pi }{2}) = 0\)
c) Biểu thức \(y''(\frac{\pi }{2}) = 0\)
d) Biểu thức \({y^{(2024)}} = \sin (x + 1012\pi )\)
Sử dụng công thức tính đạo hàm của hàm số lượng giác
a) \(y' = (\sin x)' = cosx\)
b) \(y'(\frac{\pi }{2}) = \cos \frac{\pi }{2} = 0\)
c) \(\begin{array}{l}y'' = \left( {cosx} \right)' = - \sin x\\y''\left( {\frac{\pi }{2}} \right) = - 1\end{array}\)
d) \(\begin{array}{l}{y^{(n)}} = \sin (x + n\frac{\pi }{2})\\{y^{(2024)}} = \sin (x + 1012\pi )\end{array}\)
Tính giới hạn: \(\mathop {lim}\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}}\).
Sử dụng phương pháp nhân liên hợp và phân tích thành nhân tử.
\(\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt {4x + 1} - 3}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {\sqrt {4x + 1} - 3} \right)\left( {\sqrt {4x + 1} + 3} \right)}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{(4x + 1) - 9}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}}\)
\( = \mathop {\lim }\limits_{x \to 2} \frac{{4x - 8}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{4(x - 2)}}{{\left( {x - 2} \right)\left( {\sqrt {4x + 1} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{4}{{\sqrt {4x + 1} + 3}} = \frac{4}{{\sqrt {4.2 + 1} + 3}} = \frac{2}{3}\).
Cho hàm số: \(y = {\left( {{x^4} - 1} \right)^4}\). Tính \(y'(1)\)
Sử dụng công thức tính đạo hàm của hàm hợp
\(\begin{array}{l}y' = \left[ {{{\left( {{x^4} - 1} \right)}^4}} \right]' = 4.{\left( {{x^4} - 1} \right)^3}.4{x^3} = 16{x^3}{\left( {{x^4} - 1} \right)^3}\\y'(1) = 0\end{array}\)
Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 3x + 2}}{{x - 1}}\,\,\,\;khi\,\,x \ne 1\\1 - mx\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\)liên tục tại điểm\({x_0} = 1\)
Bước 1:Tính \(f({x_0}) = {f_2}({x_0})\)
Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} {f_1}(x) = L\)
Bước 3: Nếu \({f_2}({x_0}) = L\) thì hàm số f(x) liên tục tại \({x_0}\)
Nếu \({f_2}({x_0}) \ne L\)thì hàm số f(x) không liên tục tại \({x_0}\).
(Đối với bài toán tìm tham số m để hàm số liên tục tại x0, ta thay bước 3 thành: Giải phương trình L = f2(x0), tìm m)
Hàm số đã cho xác định trên R
Ta có: \(f(1) = 1 - m\)
\(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x - 1)(x - 2)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (x - 2) = - 1\)
Để hàm số liên tục tại x = 1 khi \(f(1) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} - 3x + 2}}{{x - 1}} \Leftrightarrow 1 - m = - 1 \Leftrightarrow m = 2\)
Cho hình chóp S.ABCD đáy là hình vuông cạnh a , cạnh bên SA \( \bot \)(ABCD) và
SA = a\(\sqrt 2 \). Tính tan của góc giữa hai mp (SBC) và (ABCD).
Sử dụng phương pháp tính góc giữa hai mặt phẳng
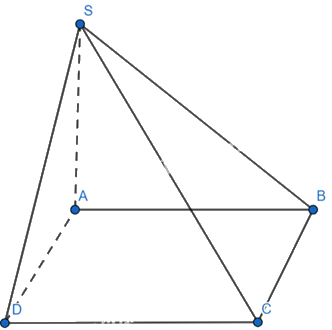
\(\begin{array}{l}\left\{ \begin{array}{l}BC \bot AB\,\\BC \bot SA\,\,(Do\,\,SA \bot (ABCD))\\AB,SA \subset (SAB)\\AB \cap SA\end{array} \right. \Rightarrow BC \bot (SAB)\\ \Rightarrow BC \bot SB\end{array}\)\(SA \bot (ABCD) \Rightarrow SA \bot AB\)
Ta có: \(\left\{ \begin{array}{l}(SBC) \cap (ABCD) = BC\\SB \subset (SBC),SB \bot BC\\AB \subset (ABCD),AB \bot BC\end{array} \right. \Rightarrow \left( {(SBC),(ABCD)} \right) = (SB,AB)\)
Do \(SA \bot (ABCD) \Rightarrow SA \bot AB\). Xét tam giác SAB vuông tại A có:
\(\tan (SB,AB) = \tan \widehat {SBA} = \frac{{SA}}{{AB}} = \frac{{a\sqrt 2 }}{a} = \sqrt 2 \)
Cho hàm số \(y = \frac{{2x - 1}}{{x + 1}}\). Tìm tọa độ điểm M thuộc đồ thị sao cho khoảng cách từ điểm \(I( - 1;2)\)tới tiếp tuyến của đồ thị tại M là lớn nhất.
Lập biểu thức tính khoảng cách từ điểm \(I( - 1;2)\) tới tiếp tuyển của đồ thị
Sử dụng BĐT Cauchy để tìm giá trị lớn nhất của biểu thức
Giả sử \(M({x_0};2 - \frac{3}{{{x_0} + 1}}) \in (C)\). PTTT của (C) tại M là:
\(y = \frac{3}{{{{({x_0} + 1)}^2}}}(x - {x_0}) + 2 - \frac{3}{{{x_0} + 1}}\,\,\,(\Delta )\)
Hay \(\begin{array}{l}(\Delta ):\,\,\,\frac{3}{{{{({x_0} + 1)}^2}}}x - y + \left[ {\frac{{3{x_0}}}{{{{({x_0} + 1)}^2}}} + 2 - \frac{3}{{{x_0} + 1}}} \right] = 0\,\,\,\\(\Delta ):\,\frac{3}{{{{({x_0} + 1)}^2}}}x - y + 2 - \frac{3}{{{{({x_0} + 1)}^2}}} = 0\\d(I,\Delta ) = \frac{{|\frac{3}{{{{({x_0} + 1)}^2}}}{x_0} - (2 - \frac{3}{{{x_0} + 1}}) + 2 - \frac{3}{{{{({x_0} + 1)}^2}}}|}}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^4}}} + 1} }} = \frac{{6|{x_0} + 1|}}{{\sqrt {9 + {{({x_0} + 1)}^4}} }} = \frac{6}{{\sqrt {\frac{9}{{{{({x_0} + 1)}^2}}} + {{({x_0} + 1)}^2}} }}\end{array}\)
Áp dụng BĐT Cauchy: \(\frac{9}{{{{({x_0} + 1)}^2}}} + {({x_0} + 1)^2} \ge 2\sqrt 9 = 6 \Rightarrow d \le \sqrt 6 \)
Dấu “=” xảy ra khi \(\frac{9}{{{{({x_0} + 1)}^2}}} = {({x_0} + 1)^2} \Leftrightarrow {x_0} = - 1 \pm \sqrt 3 \)
Vậy có hai điểm cần tìm là \(M( - 1 + \sqrt 3 ;2 - \sqrt 3 )\) hoặc \(M( - 1 - \sqrt 3 ;2 + \sqrt 3 )\)
Với mức tiêu thụ thức ăn cho cá hàng ngày của hộ gia đình A không đổi như dự định thì lượng thức ăn dự trữ sẽ hết sau 50 ngày. Nhưng trên thực tế, mức tiêu thụ thức ăn tăng thêm 3% từ ngày đầu tiên và cứ tiếp tục như vậy, ngày sau tăng thêm 3% so với ngày kề trước đó. Hỏi thực tế, lượng thức ăn dự trữ đó sẽ hết sau bao nhiêu ngày? (làm tròn đến hàng đơn vị).
Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(M{(1 + r\% )^{k - 1}},k \in N*\)
Trong đó:
M: là lượng thứ ăn trang trại ăn hết trong mỗi ngày
r (%): là % mức tiêu thụ thức ăn tăng thêm mỗi ngày
Theo dự định, mỗi ngày, trang trại ăn hết: \(1:50 = \frac{1}{{50}}\)(lượng thức ăn)
Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là: \(\frac{1}{{50}}{(1 + 3\% )^{k - 1}},k \in N*\)
Xác định số tự nhiên n nhỏ nhât để:
\(\begin{array}{l}\frac{1}{{50}} + \frac{1}{{50}}(1 + 3\% ) + \frac{1}{{50}}{(1 + 3\% )^2} + ... + \frac{1}{{50}}{(1 + 3\% )^{n - 1}} \ge 1\\ \Leftrightarrow \frac{1}{{50}}(1 + 1,03 + 1,{03^2} + ... + 1,{03^{n - 1}}) \ge 1\\ \Leftrightarrow \frac{1}{{50}}.\frac{{1,{{03}^{n - 1}} - 1}}{{1,03 - 1}} \ge 1 \Leftrightarrow 1,{03^{n - 1}} - 1 \ge 1,5 \Leftrightarrow 1,{03^{n - 1}} \ge 2,5 \Leftrightarrow n - 1 \ge {\log _{1,03}}2,5 \Leftrightarrow n \ge 31,99 \Rightarrow {n_{Min}} = 32\end{array}\)
Đề thi học kì 2 Toán 11 Cánh diều - Đề số 2: Tổng quan và Hướng dẫn Ôn tập
Học kì 2 Toán 11 là giai đoạn quan trọng, đánh dấu sự chuyển đổi từ kiến thức cơ bản lên các khái niệm nâng cao hơn. Việc chuẩn bị kỹ lưỡng cho kỳ thi học kì là điều cần thiết để đảm bảo kết quả tốt nhất. Đề thi học kì 2 Toán 11 Cánh diều - Đề số 2 do tusach.vn cung cấp là một công cụ hỗ trợ đắc lực cho quá trình ôn tập của bạn.
Cấu trúc Đề thi
Đề thi này được xây dựng theo cấu trúc đề thi học kì 2 Toán 11 của Bộ Giáo dục và Đào tạo, bao gồm các phần:
- Phần trắc nghiệm: Kiểm tra kiến thức cơ bản và khả năng nhận biết các khái niệm toán học.
- Phần tự luận: Đánh giá khả năng vận dụng kiến thức để giải quyết các bài toán phức tạp hơn.
Nội dung Đề thi
Đề thi bao gồm các chủ đề chính sau:
- Hàm số lượng giác: Các khái niệm về hàm số lượng giác, đồ thị hàm số lượng giác, phương trình lượng giác.
- Đạo hàm: Khái niệm đạo hàm, các quy tắc tính đạo hàm, ứng dụng của đạo hàm trong việc khảo sát hàm số.
- Giới hạn: Khái niệm giới hạn, các tính chất của giới hạn, tính giới hạn của hàm số.
- Hình học giải tích: Phương trình đường thẳng, phương trình đường tròn, đường conic.
- Phép biến hình: Phép tịnh tiến, phép quay, phép dời hình, phép đồng dạng.
Tại sao nên chọn Đề thi học kì 2 Toán 11 Cánh diều - Đề số 2 của tusach.vn?
- Chất lượng: Đề thi được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và độ khó phù hợp.
- Đáp án chi tiết: Kèm theo đề thi là đáp án chi tiết, giúp bạn hiểu rõ cách giải và tự đánh giá kết quả.
- Dễ dàng tải về: Bạn có thể dễ dàng tải đề thi về máy tính hoặc điện thoại để ôn tập mọi lúc mọi nơi.
- Miễn phí: Đề thi được cung cấp hoàn toàn miễn phí tại tusach.vn.
Hướng dẫn Ôn tập hiệu quả
Để đạt kết quả tốt nhất trong kỳ thi học kì 2 Toán 11, bạn nên:
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các công thức và định lý quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng đề.
- Sử dụng đề thi thử: Làm các đề thi thử để đánh giá trình độ và xác định những kiến thức còn yếu.
- Hỏi thầy cô giáo: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo để được giải đáp.
Bảng so sánh các dạng bài tập thường gặp
| Dạng bài tập | Mức độ khó | Lời khuyên |
|---|---|---|
| Giải phương trình lượng giác | Trung bình | Nắm vững các công thức lượng giác cơ bản. |
| Khảo sát hàm số bằng đạo hàm | Khó | Luyện tập nhiều bài tập về đạo hàm. |
| Tính giới hạn của hàm số | Trung bình - Khó | Hiểu rõ các quy tắc tính giới hạn. |
Tusach.vn hy vọng rằng Đề thi học kì 2 Toán 11 Cánh diều - Đề số 2 sẽ là một người bạn đồng hành hữu ích trên con đường chinh phục môn Toán của bạn. Chúc bạn ôn tập tốt và đạt kết quả cao trong kỳ thi sắp tới!