Đề thi học kì 2 Toán 9 - Đề số 4
Tổng quan nội dung
Đề thi học kì 2 Toán 9 - Đề số 4
Chào mừng các em học sinh lớp 9 đến với Đề thi học kì 2 Toán 9 - Đề số 4 do tusach.vn biên soạn.
Đề thi này được thiết kế bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề bài
Giá trị của hàm số \(y = \frac{1}{2}{x^2}\), tại \(x = 2\) là
- A.
– 2.
- B.
2.
- C.
-1.
- D.
1.
Cho phương trình \(3{x^2} - 10x + 3 = 0\,\) có hai nghiệm \({x_1};{x_2}\) mà \({x_1} < {x_2}\) . Giá trị biểu thức \(3{x_1} + {x_2}\) bằng
- A.
\(2\).
- B.
\(3\).
- C.
\(4\).
- D.
\(\frac{{28}}{3}\).
Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình:
\({x^2} - 6x + 5 = 0\).
- A.
\(\frac{1}{6}\).
- B.
3.
- C.
6.
- D.
7.
Quay 150 lần một tấm bìa hình tròn được chia thành 4 hình quạt với các màu xanh, đỏ, tím, vàng. Quan sát mũi tên chỉ vào hình quạt màu gì và ghi lại, thu được kết quả như sau:
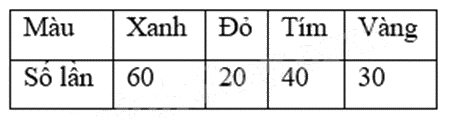
Ước lượng xác suất mũi tên chỉ vào hình quạt màu vàng là:
- A.
30%.
- B.
15%.
- C.
60%.
- D.
20%.
Bạn Hà gieo một con xúc xắc liên tiếp hai lần. Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là \(7\)” có số kết quả thuận lợi là
- A.
\(2\).
- B.
\(3\).
- C.
\(6\).
- D.
\(5\).
Diện tích đường tròn ngoại tiếp tam giác ABC vuông tại A có AB = 6cm, AC = 8cm là:
- A.
\(50\pi {\rm{c}}{{\rm{m}}^{\rm{2}}}\).
- B.
\(10\pi {\rm{c}}{{\rm{m}}^{\rm{2}}}\).
- C.
\(25\pi {\rm{c}}{{\rm{m}}^{\rm{2}}}\).
- D.
\(100\pi {\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Cho hình vẽ. Biết HA là tiếp tuyến của (O); I là trung điểm của BC và \(\widehat {AHB} = 45^\circ \). Số đo \(\widehat {IOA}\) bằng?
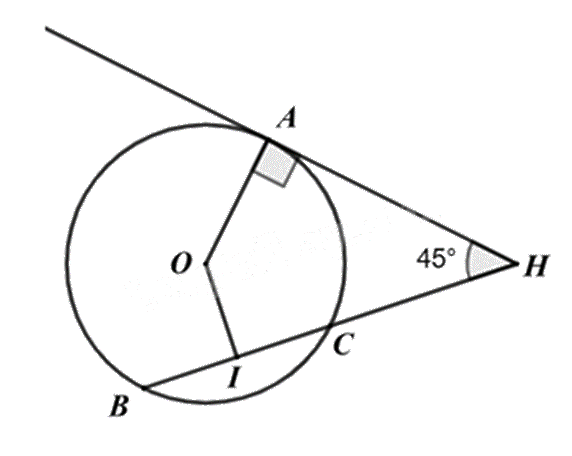
- A.
\(130^\circ \).
- B.
\(135^\circ \).
- C.
\(145^\circ \).
- D.
\(150^\circ \).
Đa giác đều là
- A.
một đa giác lồi có các góc bằng nhau.
- B.
một đa giác lồi có các cạnh bằng nhau.
- C.
một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.
- D.
một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.
Cho vòng quay mặt trời gổm 8 cabin như hình vẽ. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiểu kim đồng hổ quanh tâm bao nhiêu độ?

- A.
\(45^\circ \).
- B.
\(60^\circ \).
- C.
\(90^\circ \).
- D.
\(135^\circ \).
Cho hình trụ nội tiếp trong hình lập phương có cạnh bằng 40 cm (như hình vẽ). Khẳng định nào sau đây sai?
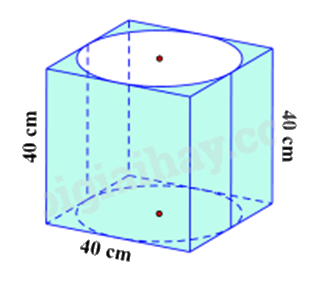
- A.
Đường kính đáy hình trụ là 20 cm.
- B.
Chiều cao của hình trụ là 40 cm.
- C.
Đường kính đáy hình trụ là 40 cm.
- D.
Cả B và C đều đúng.
Cho hình nón có đỉnh S, đường sinh \(SA = 2a\), O là tâm đường tròn đáy. Biết \(\widehat {SAO} = 60^\circ \), diện tích toàn phần của hình nón bằng:
- A.
\(4\pi {a^2}\).
- B.
\(3\pi {a^2}\).
- C.
\(2\pi {a^2}\).
- D.
\(\pi {a^2}\).
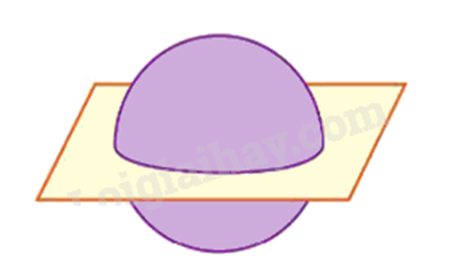
Quan sát hình sau cho biết phần chung giữa mặt phẳng và hình cầu là hình gì?

- A.
Hình vuông.
- B.
Hình chữ nhật.
- C.
Hình tròn.
- D.
Hình thang.
Một mảnh đất hình tam giác vuông có chu vi là \(60\,m\) và có cạnh huyền là \(25\,m\). Giả sử độ dài một cạnh góc vuông là \(t\,(m,\,0 < t < 25)\).
a) Tổng độ dài hai cạnh góc vuông của mảnh đất hình tam giác vuông là \(25\,\,m\).
b) Độ dài cạnh góc vuông còn lại của mảnh đất hình tam giác vuông được biểu diễn là: \(25 - t\,\,(m)\).
c) Độ dài hai cạnh góc vuông của mảnh đất hình tam giác vuông đó \(20\,m\,\,,\,\,15\,m\).
d) Trên mảnh ruộng đó người ta đem trồng lúa, mỗi mét vuông thu hoạch được \(0,8\,kg\) thóc. Số kg thóc thu hoạch được là \(240\,kg\).
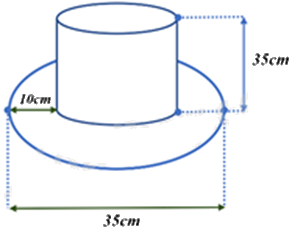
Một cái mũ bằng vải của nhà ảo thuật với kích thước như hình vẽ.
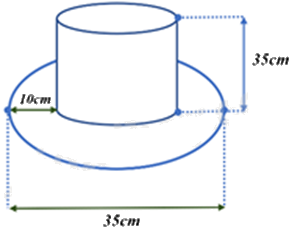
a) Bán kính đáy là 7,0cm.
b) Diện tích vải để làm ống mũ là \(581,15\pi \left( {c{m^2}} \right)\).
c) Diện tích vải để làm vành mũ là: \(240\pi \left( {c{m^2}} \right)\).
d) Tổng diện tích vải cần để làm cái mũ đó. Biết rằng tỉ lệ vải khâu (may) hao (tốn) khi may mũ là 12%. Cho biết \(\pi = 3,14\) (làm tròn đến hàng đơn vị) là \(2923\left( {c{m^2}} \right)\).
Phương trình \(2m{x^2} - \left( {2m + 1} \right)x - 3 = 0\) có nghiệm là \(x = 2\). Tính giá trị biểu thức \(A = 4{m^2} - m + 2025\).
Đáp án:
Bạn An phỏng vấn một số bạn học sinh cùng trường về loại nước uống yêu thích nhất. Kết quả được cho ở bảng sau:

Tần số tương đối biểu diễn mẫu số liệu điều tra về trà sữa là bao nhiêu phần trăm?
Đáp án:
Trong một trò chơi xúc xắc, một người chơi lần lượt gieo hai viên xúc xắc. Tính xác suất cho biến cố B: “Hai viên xúc xắc đều ra số chẵn”. (viết dưới dạng số thập phân)
Đáp án:
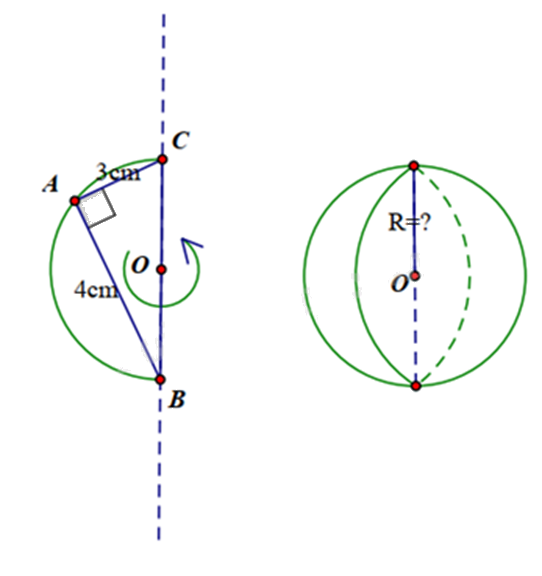
Tam giác ABC vuông tại A có AB = 4cm, AB = 3cm nội tiếp nửa đường tròn tâm O đường kính BC. Khi quay nửa hình tròn tâm O bán kính R quanh đường kính BC cố định ta thu được một hình cầu có bán kính là bao nhiêu cm? (viết dưới dạng số thập phân)
Đáp án:
a) Biết đồ thị của hàm số \(y = \left( {1 + 3a} \right){x^2}\) đi qua điểm \(M\left( { - 2;28} \right)\). Tìm a.
b) Cho phương trình \({x^2} + 2x - 2 = 0\) có hai nghiệm phân biệt \({x_1};{x_2}\). Không giải phương trình, hãy tính giá trị biểu thức \(A = {x_1}\left( {x_2^2 - 2} \right) - {x_1} - {x_2}\).
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O. Kẻ AH vuông góc với BC tại H, kẻ HE vuông góc với AB tại E, kẻ HD vuông góc với AC tại D.
a) Chứng minh tứ giác AEHD là tứ giác nội tiếp.
b) Vẽ đường kính AK của đường tròn (O). Chứng minh AE.AK = AH.AC.
Một cái thùng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của thùng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của thùng, có đỉnh là tâm của miệng thùng (xem hình minh họa). Biết rằng có 12 lít nước vào thùng thì đầy thùng (nước không chảy được vào bên trong phễu), tính thể tích của phễu.
Lời giải và đáp án
Giá trị của hàm số \(y = \frac{1}{2}{x^2}\), tại \(x = 2\) là
- A.
– 2.
- B.
2.
- C.
-1.
- D.
1.
Đáp án : B
Thay \(x = 2\) vào hàm số để tính giá trị.
Thay \(x = 2\) vào hàm số \(y = \frac{1}{2}{x^2}\) ta được:
\(y = \frac{1}{2}{.2^2} = 2\).
Đáp án B
Cho phương trình \(3{x^2} - 10x + 3 = 0\,\) có hai nghiệm \({x_1};{x_2}\) mà \({x_1} < {x_2}\) . Giá trị biểu thức \(3{x_1} + {x_2}\) bằng
- A.
\(2\).
- B.
\(3\).
- C.
\(4\).
- D.
\(\frac{{28}}{3}\).
Đáp án : C
Cách 1.(Đối với bài tập trắc nghiệm) Sử dụng máy tính cầm tay để tính hai nghiệm, sau đó thay vào biểu thức để tính giá trị.
Cách 2. Tính \(\Delta \) hoặc \(\Delta '\) của phương trình.
Biểu diễn hai nghiệm của phương trình theo \(\Delta \) hoặc \(\Delta '\).
Cách 1.
Sử dụng máy tính cầm tay ta tính được hai nghiệm của phương trình:
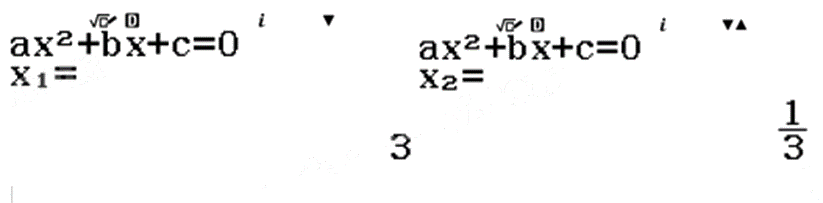
Vì \({x_1} < {x_2}\) nên \({x_1} = \frac{1}{3};{x_2} = 3\).
Giá trị biểu thức \(3{x_1} + {x_2}\) bằng: \(3.\frac{1}{3} + 3 = 4\).
Cách 2. Phương trình \(3{x^2} - 10x + 3 = 0\,\) có \(\Delta = {10^2} - 4.3.3 = 64 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1} = \frac{{10 - \sqrt {64} }}{{2.3}} = \frac{1}{3};{x_2} = \frac{{10 + \sqrt {64} }}{{2.3}} = 3\) với \({x_1} < {x_2}\).
Suy ra giá trị biểu thức \(3{x_1} + {x_2}\) bằng: \(3.\frac{1}{3} + 3 = 4\).
Đáp án C
Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình:
\({x^2} - 6x + 5 = 0\).
- A.
\(\frac{1}{6}\).
- B.
3.
- C.
6.
- D.
7.
Đáp án : C
Phương trình có dạng \({x^2} - Sx + P = 0\) là phương trình có nghiệm là hai số mà tổng của chúng bằng S và tích của chúng bằng P.
Phương trình \({x^2} - 6x + 5 = 0\) có dạng \({x^2} - Sx + P = 0\) nên tổng hai nghiệm (nếu có) của phương trình là \(S = 6\).
Đáp án C
Quay 150 lần một tấm bìa hình tròn được chia thành 4 hình quạt với các màu xanh, đỏ, tím, vàng. Quan sát mũi tên chỉ vào hình quạt màu gì và ghi lại, thu được kết quả như sau:
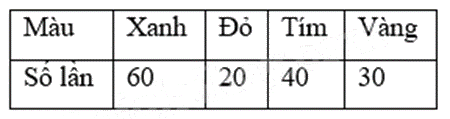
Ước lượng xác suất mũi tên chỉ vào hình quạt màu vàng là:
- A.
30%.
- B.
15%.
- C.
60%.
- D.
20%.
Đáp án : D
Từ bảng trên ta có thể ước lượng xác suất mũi tên chỉ vào hình quạt vàng bằng tỉ số giữa số lần quay vào hình quạt màu vàng với tổng số lần quay.
Số lần mũi tên chỉ vào hình quạt màu vàng là 30.
Tổng số lần quay là 150 lần.
Ước lượng xác xuất mũi tên chỉ vào hình quạt màu vàng là: \(\frac{{30}}{{150}}.100\% = 20\% \)
Đáp án D
Bạn Hà gieo một con xúc xắc liên tiếp hai lần. Biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là \(7\)” có số kết quả thuận lợi là
- A.
\(2\).
- B.
\(3\).
- C.
\(6\).
- D.
\(5\).
Đáp án : C
Xác định các kết quả có tổng bằng 7.
Các kết quả thuận lợi của biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc là \(7\)” là: (1;6), (2;5), (3;4), (4;3), (5;2), (6;1).
Vậy có 6 kết quả thuận lợi cho biến cố.
Đáp án C
Diện tích đường tròn ngoại tiếp tam giác ABC vuông tại A có AB = 6cm, AC = 8cm là:
- A.
\(50\pi {\rm{c}}{{\rm{m}}^{\rm{2}}}\).
- B.
\(10\pi {\rm{c}}{{\rm{m}}^{\rm{2}}}\).
- C.
\(25\pi {\rm{c}}{{\rm{m}}^{\rm{2}}}\).
- D.
\(100\pi {\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Đáp án : C
Tính cạnh huyền của tam giác bằng định lí Pythagore.
Bán kính đường tròn ngoại tiếp tam giác vuông bằng một nửa cạnh huyền.
Diện tích đường tròn tính bằng công thức: \(S = \pi {r^2}\)
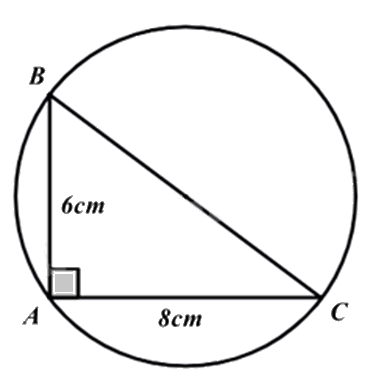
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\) suy ra \(BC = \sqrt {100} = 10\left( {cm} \right)\)
Do đó độ dài bán kính đường tròn ngoại tiếp tam giác ABC là: \(\frac{{10}}{2} = 5\left( {cm} \right)\).
Vậy diện tích đường tròn là: \(S = \pi {.5^2} = 25\pi \left( {c{m^2}} \right)\)
Đáp án C
Cho hình vẽ. Biết HA là tiếp tuyến của (O); I là trung điểm của BC và \(\widehat {AHB} = 45^\circ \). Số đo \(\widehat {IOA}\) bằng?
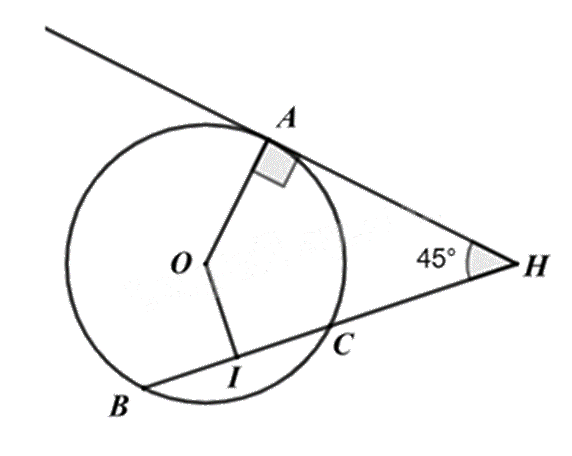
- A.
\(130^\circ \).
- B.
\(135^\circ \).
- C.
\(145^\circ \).
- D.
\(150^\circ \).
Đáp án : B
Chứng minh OAHI là tứ giác nội tiếp nên \(\widehat {IOA} + \widehat {AHI} = 180^\circ \). Ta tính được \(\widehat {IOA}\)
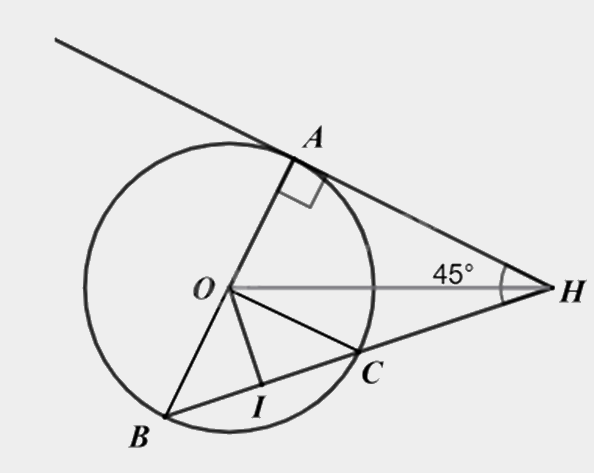
Vì HA là tiếp tuyến của (O) nên \(OA \bot AH\) suy ra tam giác OAH vuông ở A.
Do đó tam giác OAH nội tiếp đường tròn đường kính OH. (1)
Vì O cách đều hai điểm B, C (OB = OC), I cách đều hai điểm B, C (I là trung điểm của BC) nên OI là đường trung trực của BC. Suy ra \(OI \bot BC\).
Suy ra tam giác OIH vuông tại I nên tam giác OIH nội tiếp đường tròn đường kính OH. (2)
Từ (1) và (2) suy ra \(O,A,H,I\) cùng thuộc đường tròn đường kính OH hay OAHI là tứ giác nội tiếp.
Do đó \(\widehat {IOA} + \widehat {AHI} = 180^\circ \)
Suy ra \(\widehat {IOA} = 180^\circ - \widehat {AHI} = 180^\circ - 45^\circ = 135^\circ \).
Đáp án B
Đa giác đều là
- A.
một đa giác lồi có các góc bằng nhau.
- B.
một đa giác lồi có các cạnh bằng nhau.
- C.
một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.
- D.
một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.
Đáp án : C
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.
Theo khái niệm của đa giác đều thì đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.
Đáp án C
Cho vòng quay mặt trời gổm 8 cabin như hình vẽ. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiểu kim đồng hổ quanh tâm bao nhiêu độ?
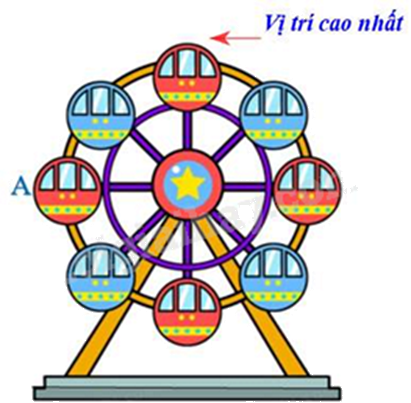
- A.
\(45^\circ \).
- B.
\(60^\circ \).
- C.
\(90^\circ \).
- D.
\(135^\circ \).
Đáp án : C
Xác định \(\alpha ^\circ \) trong phép quay thuận chiều biến điểm A thành điểm ở vị trí cao nhất.
Vì vòng quay mặt trời có 8 cabin nên là bát giác đều. Suy ra mỗi góc ở tâm có số đo là \(\frac{{360^\circ }}{8} = 45^\circ \).
Khi đó phép quay biến điểm A thành điểm ở vị trí cao nhất là: \(45^\circ .2 = 90^\circ \).
Đáp án C
Cho hình trụ nội tiếp trong hình lập phương có cạnh bằng 40 cm (như hình vẽ). Khẳng định nào sau đây sai?

- A.
Đường kính đáy hình trụ là 20 cm.
- B.
Chiều cao của hình trụ là 40 cm.
- C.
Đường kính đáy hình trụ là 40 cm.
- D.
Cả B và C đều đúng.
Đáp án : D
Quan sát hình vẽ để xác định các đặc điểm của hình trụ.
Quan sát hình vẽ ta thấy:
Chiều cao của hình trụ là 40 cm. Suy ra đáp án B đúng.
Đường kính đáy hình trụ là 40 cm. Suy ra đáp án A sai, C đúng.
Đáp án D
Cho hình nón có đỉnh S, đường sinh \(SA = 2a\), O là tâm đường tròn đáy. Biết \(\widehat {SAO} = 60^\circ \), diện tích toàn phần của hình nón bằng:
- A.
\(4\pi {a^2}\).
- B.
\(3\pi {a^2}\).
- C.
\(2\pi {a^2}\).
- D.
\(\pi {a^2}\).
Đáp án : B
Áp dụng tỉ số lượng giác vào tam giác SOA vuông tại O để tính bán kính đáy.
Sử dụng công thức tính diện tích toàn phần của hình nón: \({S_{tp}} = \pi rl + \pi {r^2}\).
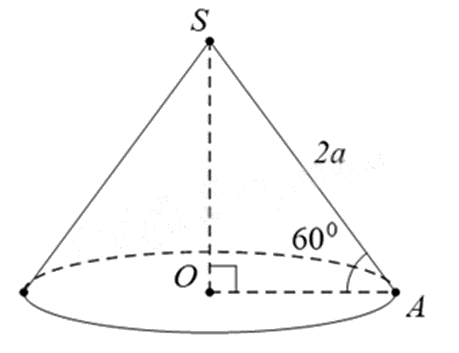
Xét tam giác SOA có SO là đường cao của hình nón nên tam giác SOA vuông tại O. Do đó:
\(\cos \widehat {SAO} = \frac{{OA}}{{SA}}\) nên \(OA = SA.\cos 60^\circ = 2a.\frac{1}{2} = a\).
Diện tích toàn phần của hình nón là:
\({S_{tp}} = \pi rl + \pi {r^2} = \pi .a.2a + \pi {a^2} = 3\pi {a^2}\).
Đáp án B
Quan sát hình sau cho biết phần chung giữa mặt phẳng và hình cầu là hình gì?
- A.
Hình vuông.
- B.
Hình chữ nhật.
- C.
Hình tròn.
- D.
Hình thang.
Đáp án : C
Dựa vào kiến thức về phần chung giữa mặt phẳng và hình cầu.
Phần chung giữa mặt phẳng và hình cầu là hình tròn.
Đáp án C
Một mảnh đất hình tam giác vuông có chu vi là \(60\,m\) và có cạnh huyền là \(25\,m\). Giả sử độ dài một cạnh góc vuông là \(t\,(m,\,0 < t < 25)\).
a) Tổng độ dài hai cạnh góc vuông của mảnh đất hình tam giác vuông là \(25\,\,m\).
b) Độ dài cạnh góc vuông còn lại của mảnh đất hình tam giác vuông được biểu diễn là: \(25 - t\,\,(m)\).
c) Độ dài hai cạnh góc vuông của mảnh đất hình tam giác vuông đó \(20\,m\,\,,\,\,15\,m\).
d) Trên mảnh ruộng đó người ta đem trồng lúa, mỗi mét vuông thu hoạch được \(0,8\,kg\) thóc. Số kg thóc thu hoạch được là \(240\,kg\).
a) Tổng độ dài hai cạnh góc vuông của mảnh đất hình tam giác vuông là \(25\,\,m\).
b) Độ dài cạnh góc vuông còn lại của mảnh đất hình tam giác vuông được biểu diễn là: \(25 - t\,\,(m)\).
c) Độ dài hai cạnh góc vuông của mảnh đất hình tam giác vuông đó \(20\,m\,\,,\,\,15\,m\).
d) Trên mảnh ruộng đó người ta đem trồng lúa, mỗi mét vuông thu hoạch được \(0,8\,kg\) thóc. Số kg thóc thu hoạch được là \(240\,kg\).
a) Từ chu vi và độ dài cạnh huyền ta tính được tổng độ dài 2 cạnh còn lại.
b) Theo ý a ta có tổng độ dài hai cạnh còn lại nên ta biểu diễn được độ dài cạnh góc vuông còn lại theo \(t\).
c) Áp dụng định lí Pythagore vào tam giác vuông để tính độ dài hai cạnh góc vuông của tam giác.
d) Sử dụng công thức tính diện tích tam giác vuông: \(S = \frac{1}{2}\). tích hai cạnh góc vuông.
Số kg thóc thu hoạch được = diện tích mảnh đất . 0,8 (kg).
a) Sai
Vì mảnh đất hình tam giác vuông có chu vi là \(60\,m\) và có cạnh huyền là \(25\,m\) nên tổng độ dài hai cạnh góc vuông của mảnh đất hình tam giác vuông là:
\(60 - 25 = 35\,(m)\).
b) Sai
Tổng độ dài hai cạnh góc vuông của mảnh đất hình tam giác vuông là \(35\,m\).
Độ dài một cạnh góc vuông là \(t\,(m,\,0 < t < 25)\).
Độ dài cạnh góc vuông còn lại của mảnh đất hình tam giác vuông được biểu diễn là: \(35 - t\,\,(m)\).
c) Đúng
Áp dụng định lí Pythagore vào tam giác vuông, ta được:
\({(35 - t)^2} + {t^2} = {25^2}\)
\({t^2} - 70t + 1225 + {t^2} = 625\)
\(2{t^2} - 70t + 600 = 0\)
\({t^2} - 35t + 300 = 0\).
Giải phương trình, ta được \({t_1} = 20\) (tmđk), \({t_2} = 15\) (tmđk)
Vậy độ dài hai cạnh góc vuông của mảnh đất hình tam giác vuông đó \(20\,m\,\,,\,\,15\,m\).
d) Sai
Diện tích mảnh ruộng hình tam giác vuông là \(\frac{1}{2} \cdot 20 \cdot 15 = 150\,({m^2})\)
Số kg thóc thu hoạch được là: \(0,8.150 = 120\,(kg)\).
Đáp án: SSĐS
Một cái mũ bằng vải của nhà ảo thuật với kích thước như hình vẽ.
a) Bán kính đáy là 7,0cm.
b) Diện tích vải để làm ống mũ là \(581,15\pi \left( {c{m^2}} \right)\).
c) Diện tích vải để làm vành mũ là: \(240\pi \left( {c{m^2}} \right)\).
d) Tổng diện tích vải cần để làm cái mũ đó. Biết rằng tỉ lệ vải khâu (may) hao (tốn) khi may mũ là 12%. Cho biết \(\pi = 3,14\) (làm tròn đến hàng đơn vị) là \(2923\left( {c{m^2}} \right)\).
a) Bán kính đáy là 7,0cm.
b) Diện tích vải để làm ống mũ là \(581,15\pi \left( {c{m^2}} \right)\).
c) Diện tích vải để làm vành mũ là: \(240\pi \left( {c{m^2}} \right)\).
d) Tổng diện tích vải cần để làm cái mũ đó. Biết rằng tỉ lệ vải khâu (may) hao (tốn) khi may mũ là 12%. Cho biết \(\pi = 3,14\) (làm tròn đến hàng đơn vị) là \(2923\left( {c{m^2}} \right)\).
a) Từ đường kính vành mũ ta tính được bán kính ống mũ.
b) Diện tích vải để làm ống mũ = diện tích xung quanh + diện tích đáy phía trên của mũ.
c) Diện tích vành mũ là diện tích hình vành khuyên: \({S_{vk}} = \pi \left( {{R^2} - {r^2}} \right)\) (\(R > r\) )
d) Tính (diện tích vải để làm ống mũ + diện tích vải để làm vành mũ).(100% + 12%).
a) Sai
Ống mũ của nhà ảo thuật là hình trụ với chiều cao 35 cm, bán kính đáy:
\(R = \frac{{35 - 2.10}}{2} = 7,5{\kern 1pt} cm\)
b) Đúng
Diện tích vải để làm ống mũ là:
\({S_1} = 2\pi Rh + \pi {R^2} = 2\pi .7,5.35 + \pi .7,{5^2} = 525\pi + 56,25\pi = 581,15\pi \;(c{m^2})\)
c) Sai
Vành mũ của nhà ảo thuật là hình vành khuyên.
Diện tích vải để làm vành mũ là:
\({S_2} = \pi .\left( {17,{5^2} - 7,{5^2}} \right) = 250\pi \;(c{m^2})\)
d) Đúng
Vậy tổng diện tích vải cần để làm cái mũ là:
\(\begin{array}{l}(581,15\pi \; + 250\pi ).\left( {100\% + 12\% } \right) = 831,15\pi .1,12\\ = 831,15.3,14.1,12 \approx 2923(c{m^2})\end{array}\)
Đáp án: SĐSĐ
Phương trình \(2m{x^2} - \left( {2m + 1} \right)x - 3 = 0\) có nghiệm là \(x = 2\). Tính giá trị biểu thức \(A = 4{m^2} - m + 2025\).
Đáp án:
Đáp án:
Thay \(x = 2\) vào phương trình. Giải phương trình để tìm m.
Thay \(x = 2\) vào phương trình, ta được:
\(\begin{array}{l}2m{.2^2} - \left( {2m + 1} \right).2 - 3 = 0\\8m - 4m - 2 - 3 = 0\\4m = 5\\m = \frac{5}{4}\end{array}\)
Thay \(m = \frac{5}{4}\) vào A, ta được:
\(\begin{array}{l}A = 4.{\left( {\frac{5}{4}} \right)^2} - \frac{5}{4} + 2025\\ = 4.\frac{{25}}{{16}} - \frac{5}{4} + 2025\\ = \frac{{25}}{4} - \frac{5}{4} + 2025\\ = 5 + 2025 = 2030\end{array}\)
Đáp án: 2030
Bạn An phỏng vấn một số bạn học sinh cùng trường về loại nước uống yêu thích nhất. Kết quả được cho ở bảng sau:

Tần số tương đối biểu diễn mẫu số liệu điều tra về trà sữa là bao nhiêu phần trăm?
Đáp án:
Đáp án:
Từ bảng tần số, xác định tần số của trà sữa, tổng tần số của các loại nước uống.
Tính tần số tương đối của trà sữa: tần số : tổng tần số.100%
Từ bảng tần số, ta thấy tần số của trà sữa là 18.
Tổng tần số của các loại nước uống là: 18 + 6 + 16 + 10 = 50
Tần số tương đối của trà sữa là: \(\frac{{18}}{{50}}.100\% = 36\% .\)
Vậy tần số tương đối của nhóm này là 36%.
Đáp án: 36
Trong một trò chơi xúc xắc, một người chơi lần lượt gieo hai viên xúc xắc. Tính xác suất cho biến cố B: “Hai viên xúc xắc đều ra số chẵn”. (viết dưới dạng số thập phân)
Đáp án:
Đáp án:
Xác định số phần tử của không gian mẫu, số kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số phần tử của không gian mẫu.
Không gian mẫu của phép thử là:
\(\Omega = \left\{ \begin{array}{l}\left( {1;1} \right),\left( {1;2} \right),\left( {1;3} \right),\left( {1;4} \right),\left( {1;5} \right),\left( {1;6} \right),\\\left( {2;1} \right),\left( {2;2} \right),\left( {2;3} \right),\left( {2;4} \right),\left( {2;5} \right),\left( {2;6} \right),\\\left( {3;1} \right),\left( {3;2} \right),\left( {3;3} \right),\left( {3;4} \right),\left( {3;5} \right),\left( {3;6} \right),\\\left( {4;1} \right),\left( {4;2} \right),\left( {4;3} \right),\left( {4;4} \right),\left( {4;5} \right),\left( {4;6} \right),\\\left( {5;1} \right),\left( {5;2} \right),\left( {5;3} \right),\left( {5;4} \right),\left( {5;5} \right),\left( {5;6} \right),\\\left( {6;1} \right),\left( {6;2} \right),\left( {6;3} \right),\left( {6;4} \right),\left( {6;5} \right),\left( {6;6} \right)\end{array} \right\}.\)
Số phần tử của không gian mẫu là 36.
Các số chẵn trên một viên xúc xắc là: 2, 4, 6.
Các kết quả thuận lợi của biến cố B: “Hai viên xúc xắc đều ra số chẵn” là:
\((2,2),(2,4),(2,6),(4,2),(4,4),(4,6),(6,2),(6,4),(6,6).\)
Có 9 kết quả thuận lợi cho biến cố B.
Do đó xác suất của biến cố B là:\(P(B) = \frac{9}{{36}} = \frac{1}{4} = 0,25\).
Đáp án: 0,25
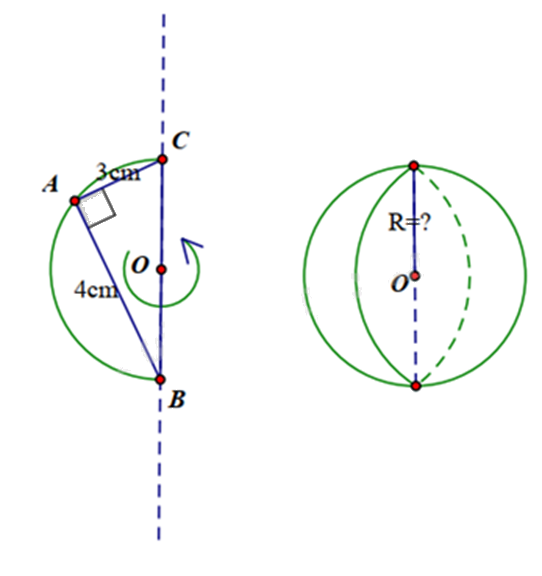
Tam giác ABC vuông tại A có AB = 4cm, AB = 3cm nội tiếp nửa đường tròn tâm O đường kính BC. Khi quay nửa hình tròn tâm O bán kính R quanh đường kính BC cố định ta thu được một hình cầu có bán kính là bao nhiêu cm? (viết dưới dạng số thập phân)
Đáp án:
Đáp án:
Sử dụng định lí Pythagore để tính đường kính hình cầu.
Từ đó ta tính được bán kính hình cầu.
Vì tam giác ABC vuông tại A nên áp dụng định lí Pythagore vào tam giác ABC, ta được:
\(B{C^2} = A{B^2} + A{C^2} = {4^2} + {3^2} = 25\) suy ra \(BC = \sqrt {25} = 5\left( {cm} \right)\)
Suy ra bán kính hình cầu là: \(OB = \frac{{BC}}{2} = \frac{5}{2} = 2,5\left( {cm} \right)\).
Đáp án: 2,5
a) Biết đồ thị của hàm số \(y = \left( {1 + 3a} \right){x^2}\) đi qua điểm \(M\left( { - 2;28} \right)\). Tìm a.
b) Cho phương trình \({x^2} + 2x - 2 = 0\) có hai nghiệm phân biệt \({x_1};{x_2}\). Không giải phương trình, hãy tính giá trị biểu thức \(A = {x_1}\left( {x_2^2 - 2} \right) - {x_1} - {x_2}\).
a) Thay toạ độ điểm \(M\left( { - 2;28} \right)\) vào hàm số \(y = \left( {1 + 3a} \right){x^2}\) để tìm a.
b) Dùng \(ac < 0\) để xác định số nghiệm của phương trình.
Tính tổng và tích của hai nghiệm \({x_1},{x_2}\) theo định lí Viète: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \frac{{ - b}}{a}\\P = {x_1}{x_2} = \frac{c}{a}\end{array} \right.\).
Biến đổi biểu thức A kết hơp định lí Viète để tính A.
a) Thay \(x = - 2;y = 28\) vào hàm số, ta được:
\(\begin{array}{l}28 = \left( {1 + 3a} \right).{\left( { - 2} \right)^2}\\4\left( {1 + 3a} \right) = 28\\1 + 3a = 7\\3a = 6\\a = 2\end{array}\)
Vậy \(a = 2\).
b) Xét phương trình \({x^2} + 2x - 2 = 0\) ta có: \(ac = 1.\left( { - 2} \right) = - 2 < 0\) nên phương trình có hai nghiệm phân biệt \({x_1};{x_2}\).
Áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = - \frac{2}{1} = - 2\\P = {x_1}.{x_2} = \frac{{ - 2}}{1} = - 2\end{array} \right.\)
Ta có: \(A = {x_1}\left( {x_2^2 - 2} \right) - {x_1} - {x_2}\)
\(\begin{array}{l} = {x_1}\left( {x_2^2 + {x_1}{x_2}} \right) - {x_1} - {x_2}\\ = {x_1}{x_2}\left( {{x_2} + {x_1}} \right) - \left( {{x_1} + {x_2}} \right)\\ = \left( { - 2} \right).\left( { - 2} \right) - \left( { - 2} \right)\\ = 4 + 2 = 6\end{array}\)
Vậy \(A = 6\).
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O. Kẻ AH vuông góc với BC tại H, kẻ HE vuông góc với AB tại E, kẻ HD vuông góc với AC tại D.
a) Chứng minh tứ giác AEHD là tứ giác nội tiếp.
b) Vẽ đường kính AK của đường tròn (O). Chứng minh AE.AK = AH.AC.
a) Chứng minh \(\Delta AEH\) và \(\Delta ADH\) cùng nội tiếp đường tròn đường kính AH nên tứ giác AEHD nội tiếp.
b) Chứng minh $\Delta AHE\backsim \Delta ABH$ suy ra \(\widehat {AHE} = \widehat {ABH}\).
Kết hợp với \(\widehat {ABH} = \widehat {AKC}\) (hai góc nội tiếp cùng chắn cung AC)
suy ra \(\widehat {AHE} = \widehat {AKC}\)
Chứng minh $\Delta EAH\backsim \Delta CAK$ suy ra \(\frac{{AE}}{{AC}} = \frac{{AH}}{{AK}}\) nên \(AE.AK = AH.AC\).
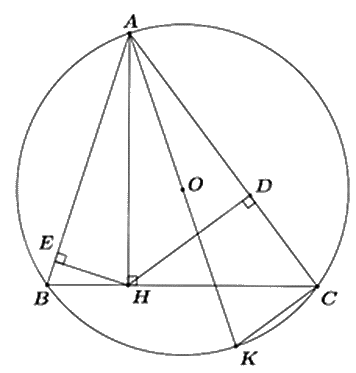
a) Xét $\Delta AEH$ vuông tại E nên $\Delta AEH$ nội tiếp đường tròn đường kính AH, do đó A, E, H thuộc đường tròn đường kính AH.
Xét $\Delta ADH$ vuông tại D nên $\Delta ADH$ nội tiếp đường tròn đường kính AH, do đó A, D, H thuộc đường tròn đường kính AH.
Do đó bốn điểm A, E, H, D thuộc đường tròn đường kính AH hay tứ giác AEHD nội tiếp đường tròn đường kính AH.
b) Vì AK là đường kính của (O) nên \(\widehat {ACK} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Xét \(\Delta AHE\) và \(\Delta ABH\) có:
\(\widehat {AEH} = \widehat {AHB}\left( { = 90^\circ } \right)\)
\(\widehat A\) chung
nên $\Delta AHE\backsim \Delta ABH$ suy ra \(\widehat {AHE} = \widehat {ABH}\).
Mà \(\widehat {ABH} = \widehat {AKC}\) (hai góc nội tiếp cùng chắn cung AC)
suy ra \(\widehat {AHE} = \widehat {AKC}\)
Xét \(\Delta EAH\) và \(\Delta CAK\) có:
\(\widehat {AEH} = \widehat {ACK}\left( { = 90^\circ } \right)\)
\(\widehat {AHE} = \widehat {AKC}\) (cmt)
nên $\Delta EAH\backsim \Delta CAK$ suy ra \(\frac{{AE}}{{AC}} = \frac{{AH}}{{AK}}\) nên \(AE.AK = AH.AC\).
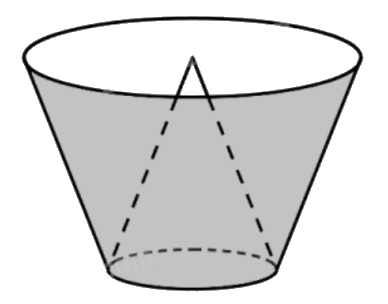
Một cái thùng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của thùng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của thùng, có đỉnh là tâm của miệng thùng (xem hình minh họa). Biết rằng có 12 lít nước vào thùng thì đầy thùng (nước không chảy được vào bên trong phễu), tính thể tích của phễu.

Gọi O là tâm của đáy, C là đỉnh, CA là một đường sinh của hình nón ban đầu.
Gọi tâm của đường tròn đáy thùng đựng nước là O’, B là một điểm thuộc đường tròn đáy sao cho B nằm trên đường sinh CA của hình nón ban đầu.
Chứng minh \(\Delta CO'B\) đồng dạng với \(\Delta CO'B\), từ đó suy ra tỉ lệ chiều cao của phễu so với hình nón ban đầu.
Gọi \(V\) là thể tích hình nón ban đầu, \({V_p}\) là thể tích phễu, \({V_t}\) là thể tích thùng chứa đầy nước.
Ta có: \(V = 2{V_p} + {V_t}\).
Áp dụng công thức tính thể tích hình nón \(V = \frac{1}{3}\pi {r^2}h\) với r là bán kính đáy, h là chiều cao để tìm \({V_p}\).

Gọi O là tâm của đáy, C là đỉnh, CA là một đường sinh của hình nón ban đầu.
Gọi O’ tâm của đường tròn đáy thùng đựng nước, B là một điểm thuộc đường tròn đáy sao cho B nằm trên đường sinh CA của hình nón ban đầu.
Xét \(\Delta CO'B\) và \(\Delta COA\), có:
\(\widehat {ACO}\) chung;
\(\widehat {CO'B} = \widehat {COA} = {90^o}\) (vì trục CO vuông góc với hai mặt phẳng đáy thùng).
Do đó \(\Delta CO'B\backsim \Delta CO'B\) (g.g), suy ra \(\frac{{CO}}{{CO'}} = \frac{{CA}}{{CB}} = \frac{{OA}}{{O'B}} = 2\) (do bán kính miệng thùng gấp hai lần bán kính đáy thùng).
Gọi \(V\) là thể tích khối nón ban đầu, \({V_p}\) là thể tích phễu, \({V_t} = 12\) là thể tích thùng chứa đầy nước.
Ta có: \(V = 2{V_p} + {V_t}\).
Mặt khác:
\(\frac{{{V_p}}}{V} = \frac{{\frac{1}{3}\pi .O'{B^2}.CO'}}{{\frac{1}{3}\pi .O{A^2}.CO}} = \frac{{\frac{1}{3}\pi .{{\left( {\frac{{OA}}{2}} \right)}^2}.\frac{{CO}}{2}}}{{\frac{1}{3}\pi .O{A^2}.CO}} = {\left( {\frac{1}{2}} \right)^2}.\frac{1}{2} = \frac{1}{8}\) hay \(V = 8{V_p}\).
Do đó: \(8{V_p} = 2{V_p} + {V_t}\) hay \(6{V_p} = {V_t} = 12\).
Vậy thể tích của phễu là 2 lít.
Tổng quan về Đề thi học kì 2 Toán 9 - Đề số 4
Đề thi học kì 2 Toán 9 đóng vai trò quan trọng trong việc đánh giá kết quả học tập của học sinh sau một học kì. Đề thi không chỉ kiểm tra kiến thức mà còn đánh giá khả năng vận dụng kiến thức vào giải quyết các bài toán thực tế. Đề thi học kì 2 Toán 9 - Đề số 4 của tusach.vn được xây dựng với mục tiêu cung cấp một công cụ ôn tập hiệu quả cho học sinh.
Cấu trúc đề thi
Đề thi học kì 2 Toán 9 - Đề số 4 thường bao gồm các dạng bài tập sau:
- Đại số: Giải phương trình bậc hai, hệ phương trình, bất phương trình, hàm số bậc nhất và hàm số bậc hai.
- Hình học: Chứng minh các tính chất của đường tròn, tam giác, tứ giác nội tiếp, các định lý về tam giác đồng dạng.
- Bài tập thực tế: Các bài toán ứng dụng kiến thức toán học vào các tình huống thực tế.
Tại sao nên luyện tập với Đề thi học kì 2 Toán 9 - Đề số 4 của tusach.vn?
Có rất nhiều lý do để bạn chọn luyện tập với đề thi của chúng tôi:
- Đề thi được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm: Đảm bảo tính chính xác và phù hợp với chương trình học.
- Đáp án chi tiết, dễ hiểu: Giúp học sinh tự đánh giá kết quả và rút kinh nghiệm.
- Đa dạng các dạng bài tập: Rèn luyện kỹ năng giải toán một cách toàn diện.
- Miễn phí tải về: Tiết kiệm chi phí cho học sinh và phụ huynh.
Hướng dẫn giải một số dạng bài tập thường gặp
Giải phương trình bậc hai
Để giải phương trình bậc hai ax2 + bx + c = 0, ta có thể sử dụng công thức nghiệm:
x = (-b ± √(b2 - 4ac)) / 2a
Lưu ý, nếu b2 - 4ac < 0 thì phương trình vô nghiệm.
Chứng minh các tính chất của đường tròn
Khi chứng minh các tính chất của đường tròn, cần nắm vững các định lý và tính chất cơ bản, ví dụ:
- Góc nội tiếp bằng nửa góc ở tâm cùng chắn một cung.
- Hai dây cung song song thì hai cung bị chắn tương ứng bằng nhau.
Lời khuyên khi làm bài thi
Để đạt kết quả tốt nhất trong kỳ thi học kì 2 Toán 9, bạn nên:
- Ôn tập kỹ lý thuyết và các công thức quan trọng.
- Luyện tập thường xuyên với các đề thi thử.
- Đọc kỹ đề bài trước khi làm.
- Sử dụng thời gian hợp lý cho từng câu hỏi.
- Kiểm tra lại bài làm sau khi hoàn thành.
Tải Đề thi học kì 2 Toán 9 - Đề số 4 ngay hôm nay!
Đừng bỏ lỡ cơ hội luyện tập và nâng cao kiến thức với Đề thi học kì 2 Toán 9 - Đề số 4 của tusach.vn. Hãy tải đề thi ngay hôm nay để chuẩn bị tốt nhất cho kỳ thi sắp tới!
| Dạng bài | Mức độ khó | Điểm |
|---|---|---|
| Giải phương trình | Trung bình | 2 |
| Chứng minh hình học | Khó | 3 |
| Bài tập ứng dụng | Dễ | 1 |
| Tổng điểm: 6 | ||