Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 5
Tổng quan nội dung
Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 5
Tusach.vn xin giới thiệu Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 5, một tài liệu ôn tập quan trọng dành cho học sinh lớp 9. Đề thi này được biên soạn bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, bao phủ các chủ đề chính trong chương trình học kì 1. Đi kèm với đề thi là đáp án chi tiết, giúp học sinh tự kiểm tra và đánh giá kết quả học tập.
Đề bài
Phương trình \(2x + y = 1\) kết hợp với phương trình nào dưới đây để được một hệ phương trình bậc nhất hai ẩn?
- A.
\(2x + 3{y^2} = 0\).
- B.
\(xy - x = 1\).
- C.
\(3x + 2{y^3} = 1\).
- D.
\(3x - y = 5\).
Điều kiện xác định của phương trình \(\frac{{4x - 5}}{{x - 1}} = 2x + \frac{1}{{{x^2}}}\) là
- A.
\(x \ne 1;x \ne 0\).
- B.
\(x \ne - 1\) và \(x \ne 0\).
- C.
\(x \ne 1\).
- D.
\(x \ne 0\).
Bất phương trình \( - x - 2 > 4\), phép biến đổi nào sau đây là đúng?
- A.
\(x > 4 + 2\).
- B.
\(x < 4 - 2\).
- C.
\(x < - 4 - 2\).
- D.
\(x < - 4 + 2\).
Cho số thực \(a > 0\). Số nào sau đây là căn bậc hai số học của a?
- A.
\(2\sqrt a \).
- B.
\(\sqrt a \).
- C.
\(\sqrt {2a} \).
- D.
\( - \sqrt a \).
Rút gọn biểu thức \(\frac{2}{5}.\sqrt {25} - \frac{9}{2}.\sqrt {\frac{{16}}{{81}}} + \sqrt {169} \) ta được kết quả là
- A.
15.
- B.
14.
- C.
13.
- D.
12.
Thu gọn \(\sqrt[3]{{125{a^3}}}\) ta được
- A.
\( - 5a\).
- B.
\(25a\).
- C.
\( - 25{a^3}\).
- D.
\(5a\).
Cho tam giác ABC vuông tại A có \(AC = 5cm,\widehat B = 30^\circ \). Độ dài BC là
- A.
\(5,5cm\).
- B.
\(5cm\).
- C.
\(10cm\).
- D.
\(5\sqrt 2 cm\).
Cho đường tròn \(\left( {O;3cm} \right)\) và hai điểm A, B sao cho \(OA = OB = 3cm\). Khi đó
- A.
Điểm A nằm trong (O), điểm B nằm trên (O).
- B.
Điểm A và B đối xứng với nhau qua tâm O.
- C.
Điểm A và B đều nằm trên đường tròn (O).
- D.
\(AB = 6cm\) là đường kính của đường tròn (O).
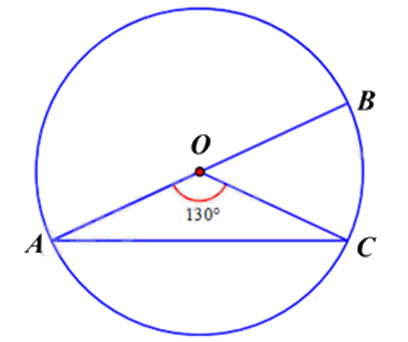
Cho đường tròn (O) có AB là đường kính. Lấy C là điểm thuộc cung cung AB biết \(\widehat {AOC} = 130^\circ \). Số đo cung nhỏ \(BC\) là:
- A.
\(360^\circ \).
- B.
\(230^\circ \).
- C.
\(130^\circ \).
- D.
\(50^\circ \).
Độ dài cung tròn \(60^\circ \) của đường tròn đường kính 6dm là
- A.
\(\pi \left( {dm} \right)\).
- B.
\(2\pi \left( {dm} \right)\).
- C.
\(36\pi \left( {dm} \right)\).
- D.
\(12\pi \left( {dm} \right)\).
Cho hai đường tròn \(\left( {O;20cm} \right)\) và \(\left( {O';15cm} \right)\) cắt nhau. Khi đó
- A.
\(OO' < 5cm\).
- B.
\(5cm < OO' < 35cm\).
- C.
\(OO' > 35cm\).
- D.
\(OO' = 35cm\).
Cho hai tiếp tuyến PA và PB của đường tròn (O) (A, B là hai tiếp điểm). Biết \(\widehat {APB} = 60^\circ \), khi đó \(\widehat {APO}\) bằng
- A.
\(120^\circ \).
- B.
\(60^\circ \).
- C.
\(20^\circ \).
- D.
\(30^\circ \).
Cho biểu thức \(A = \left( {\frac{1}{{\sqrt a + 1}} - \frac{1}{{\sqrt a + a}}} \right):\frac{{\sqrt a - 1}}{{2\sqrt a + a + 1}}\) \(\left( {a > 0;a \ne 1} \right)\).
a) \(A = \frac{{\sqrt a + 1}}{{\sqrt a }}\).
b) Giá trị của A khi \(a = 4\) là \(\frac{3}{2}\).
c) Khi \(a \ge 1\) thì \(\sqrt a .A \ge 2\).
d) Có \(0\) giá trị nguyên của \(a\) để \(A\) nguyên.
Một trường trung học mua \(878\) quyển vở bao gồm \(x\) quyển vở loại thứ nhất và \(y\) quyển vở loại thứ hai (\(x,y \in \mathbb{N}\)). Giá bán mỗi quyển vở loại thứ nhất và loại thứ hai lần lượt là \(7500\) và \(12600\) đồng. Biết tổng số tiền nhà trường đã dùng để mua \(878\) quyển vở là \(9073800\) đồng. Mỗi học sinh xuất sắc được thưởng \(3\) quyển vở loại thứ nhất và \(4\) quyển vở loại thứ hai. Mỗi học sinh giỏi được thưởng \(2\) quyển vở loại thứ nhất và \(2\) quyển vở loại thứ hai, các học sinh khác không được thưởng, tổng số học sinh giỏi và xuất sắc chiếm \(20\% \) số học sinh toàn trường.
a) \(x + y = 878\).
b) \(75x + 126y = 9073800\).
c) \(x = 391\), \(y = 488\).
d) Tổng số học sinh của trường là \(749\).
Một trường trung học dự định tổ chức chuyến tham quan học tập thực tế cho học sinh khối 9 tại một bảo tàng và công viên khoa học (Science Park) trong 1 ngày (trong ngày từ 7h00 đến 17h00). Tổng kinh phí nhà trường dự trù là 20 triệu đồng, bao gồm chi phí thuê xe đưa đón và bữa ăn cho học sinh. Gọi \(x\) là số bạn có thể tham gia chuyến tham quan. (học sinh, \(x > 0\))
• Giá thuê xe là 5 triệu đồng/ngày.
• Vé vào cổng mỗi học sinh là 30 000 đồng.
• Bữa ăn trưa cho mỗi học sinh có giá 50 000 đồng.
a) Chi phí cho mỗi học sinh là 80 000 đồng.
b) Tổng chi phí nhà trường cần trả cho chuyến tham quan có \(x\) bạn là \(80\,000x\).
c) \(80\,000x + 5\,000\,000 \le 20\,000\,000\).
d) Trường có thể tổ chức cho tối đa 188 học sinh tham gia chuyến tham quan này.
Cho tam giác MNP có MN = 5cm, NP = 12cm, MP = 13cm. Vẽ đường tròn \(\left( {M;MN} \right)\), gọi Q là giao điểm của đường tròn với MP.
a) NP là tiếp tuyến của \(\left( {M;MN} \right)\).
b) \(\widehat {NPM} \approx 30^\circ \).
c) sđ$\overset\frown{NQ}\approx 67{}^\circ $.
d) \(\widehat {PNQ} \approx 35^\circ \).
Phương trình \(x\left( {x - 5} \right) + 2\left( {x - 5} \right) = 0\) có tổng hai nghiệm bằng:
Đáp án:
Giá trị của biểu thức \(\sqrt {\frac{3}{5}} - \sqrt {\frac{5}{3}} + \frac{{\sqrt {60} }}{{15}}\) có kết quả bằng:
Đáp án:
Tổng các giá trị của x để \(\sqrt {{x^2} - 6x + 9} = 2\) là:
Đáp án:
Cho hai đường tròn \(\left( {A;3cm} \right)\) và \(\left( {B;5cm} \right)\) đựng nhau. Gọi M, N lần lượt là giao điểm của AB với \(\left( {A;3cm} \right)\). Gọi C, D lần lượt là giao điểm của AB với \(\left( {B;5cm} \right)\) sao cho C, M nằm cùng phía đối với A còn N, D nằm cùng phía đối với B. Tổng ND + CM là bao nhiêu cm?
Đáp án:
Một đầu của cần gạt nước được cố định tại điểm O. Khi đầu còn lại của cần gạt xoay \(60^\circ \), nó sẽ quét được một vùng có diện tích bằng \(\frac{8}{3}\pi \left( {{m^2}} \right)\).
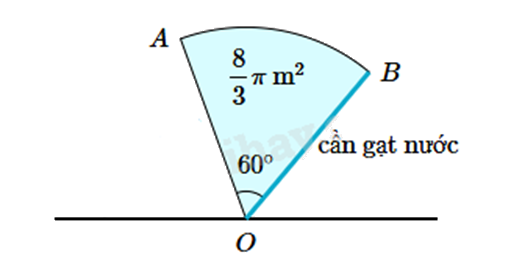
Chiều dài của cần gạt nước là bao nhiêu m?
Đáp án:
Cho \(\alpha \) là góc nhọn bất kì. Khi đó \(C = {\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha .{\cos ^2}\alpha \) có giá trị bằng:
Đáp án:
Lời giải và đáp án
Phương trình \(2x + y = 1\) kết hợp với phương trình nào dưới đây để được một hệ phương trình bậc nhất hai ẩn?
- A.
\(2x + 3{y^2} = 0\).
- B.
\(xy - x = 1\).
- C.
\(3x + 2{y^3} = 1\).
- D.
\(3x - y = 5\).
Đáp án : D
Hệ phương trình bậc nhất hai ẩn là hệ bao gồm hai phương trình bậc nhất hai ẩn.
Vì phương trình \(3x - y = 5\) là phương trình bậc nhất hai ẩn nên kết hợp với phương trình \(2x + y = 1\) ta được hệ phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}2x + y = 1\\3x - y = 5\end{array} \right.\).
Đáp án D
Điều kiện xác định của phương trình \(\frac{{4x - 5}}{{x - 1}} = 2x + \frac{1}{{{x^2}}}\) là
- A.
\(x \ne 1;x \ne 0\).
- B.
\(x \ne - 1\) và \(x \ne 0\).
- C.
\(x \ne 1\).
- D.
\(x \ne 0\).
Đáp án : A
Điều kiện xác định của phương trình chứa ẩn ở mẫu là mẫu thức khác 0.
Điều kiện xác định của phương trình \(\frac{{4x - 5}}{{x - 1}} = 2x + \frac{1}{{{x^2}}}\) là \(x - 1 \ne 0\) và \({x^2} \ne 0\).
Suy ra \(x \ne 1;x \ne 0\).
Đáp án A
Bất phương trình \( - x - 2 > 4\), phép biến đổi nào sau đây là đúng?
- A.
\(x > 4 + 2\).
- B.
\(x < 4 - 2\).
- C.
\(x < - 4 - 2\).
- D.
\(x < - 4 + 2\).
Đáp án : C
Sử dụng tính chất của bất đẳng thức để biến đổi bất phương trình.
Ta có:
\(\begin{array}{l} - x - 2 > 4\\ - x > 4 + 2\\x < - 4 - 2\end{array}\)
Đáp án C
Cho số thực \(a > 0\). Số nào sau đây là căn bậc hai số học của a?
- A.
\(2\sqrt a \).
- B.
\(\sqrt a \).
- C.
\(\sqrt {2a} \).
- D.
\( - \sqrt a \).
Đáp án : B
Sử dụng khái niệm căn bậc hai số học của một số.
Căn bậc hai số học của một số thực a > 0 là \(\sqrt a \).
Đáp án B
Rút gọn biểu thức \(\frac{2}{5}.\sqrt {25} - \frac{9}{2}.\sqrt {\frac{{16}}{{81}}} + \sqrt {169} \) ta được kết quả là
- A.
15.
- B.
14.
- C.
13.
- D.
12.
Đáp án : C
Sử dụng kiến thức về căn bậc hai để rút gọn.
\(\begin{array}{l}\frac{2}{5}.\sqrt {25} - \frac{9}{2}.\sqrt {\frac{{16}}{{81}}} + \sqrt {169} \\ = \frac{2}{5}.5 - \frac{9}{2}.\frac{4}{9} + 13\\ = 2 - 2 + 13\\ = 13\end{array}\)
Đáp án C
Thu gọn \(\sqrt[3]{{125{a^3}}}\) ta được
- A.
\( - 5a\).
- B.
\(25a\).
- C.
\( - 25{a^3}\).
- D.
\(5a\).
Đáp án : D
Sử dụng kiến thức về căn thức bậc ba.
\(\sqrt[3]{{125{a^3}}} = \sqrt[3]{{{{\left( {5a} \right)}^3}}} = 5a\).
Đáp án D
Cho tam giác ABC vuông tại A có \(AC = 5cm,\widehat B = 30^\circ \). Độ dài BC là
- A.
\(5,5cm\).
- B.
\(5cm\).
- C.
\(10cm\).
- D.
\(5\sqrt 2 cm\).
Đáp án : C
Sử dụng hệ thức lượng liên quan đến cạnh đối và cạnh huyền để tính BC.
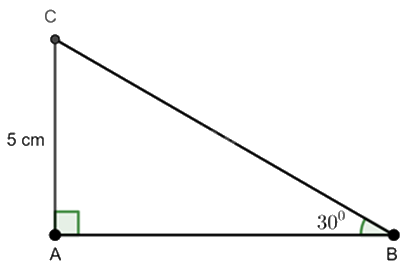
Xét tam giác ABC vuông tại A có \(\widehat B = 30^\circ \) nên ta có:
\(\sin B = \frac{{AC}}{{BC}}\) suy ra \(BC = \frac{{AC}}{{\sin B}} = \frac{5}{{\sin 30^\circ }} = 10\left( {cm} \right)\)
Đáp án C
Cho đường tròn \(\left( {O;3cm} \right)\) và hai điểm A, B sao cho \(OA = OB = 3cm\). Khi đó
- A.
Điểm A nằm trong (O), điểm B nằm trên (O).
- B.
Điểm A và B đối xứng với nhau qua tâm O.
- C.
Điểm A và B đều nằm trên đường tròn (O).
- D.
\(AB = 6cm\) là đường kính của đường tròn (O).
Đáp án : C
Dựa vào kiến thức về vị trí tương đối của điểm và đường tròn.
Vì OA = OB = R nên điểm A và B nằm trên (O), do đó A sai, C đúng.
Vì theo đề bài, điểm O không nằm giữa A và B nên A và B không đối xứng với nhau qua O và AB không phải đường kính của (O), do đó B, D sai.
Đáp án C
Cho đường tròn (O) có AB là đường kính. Lấy C là điểm thuộc cung cung AB biết \(\widehat {AOC} = 130^\circ \). Số đo cung nhỏ \(BC\) là:
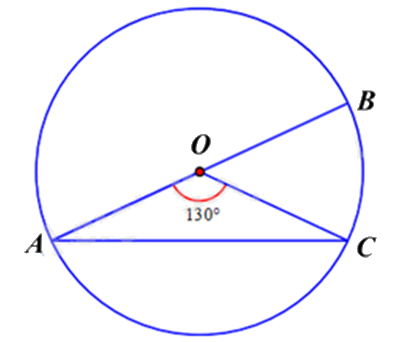
- A.
\(360^\circ \).
- B.
\(230^\circ \).
- C.
\(130^\circ \).
- D.
\(50^\circ \).
Đáp án : D
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Số đo cung nhỏ BC chính là số đo góc ở tâm \(\widehat {BOC}\).
Vì AB là đường kính của đường tròn (O) nên \(\widehat {AOB} = 180^\circ \).
Mà \(\widehat {AOB} = \widehat {AOC} + \widehat {COB}\) suy ra \(\widehat {BOC} = \widehat {AOB} - \widehat {AOC} = 180^\circ - 130^\circ = 50^\circ \).
Đáp án D
Độ dài cung tròn \(60^\circ \) của đường tròn đường kính 6dm là
- A.
\(\pi \left( {dm} \right)\).
- B.
\(2\pi \left( {dm} \right)\).
- C.
\(36\pi \left( {dm} \right)\).
- D.
\(12\pi \left( {dm} \right)\).
Đáp án : A
Sử dụng công thức tính độ dài cung tròn: \(l = \frac{{\pi Rn}}{{180}}\).
Bán kính đường tròn là: \(6:2 = 3\left( {dm} \right)\)
Độ dài cung tròn \(60^\circ \) của đường tròn là:
\(l = \frac{{\pi .3.60}}{{180}} = \pi \left( {dm} \right)\).
Đáp án A
Cho hai đường tròn \(\left( {O;20cm} \right)\) và \(\left( {O';15cm} \right)\) cắt nhau. Khi đó
- A.
\(OO' < 5cm\).
- B.
\(5cm < OO' < 35cm\).
- C.
\(OO' > 35cm\).
- D.
\(OO' = 35cm\).
Đáp án : B
Hai đường tròn (O; R) và (O’; r) (với R > r) cắt nhau khi \(R - r < OO' < R + r\).
Vì hai đường tròn \(\left( {O;20cm} \right)\) và \(\left( {O';15cm} \right)\) cắt nhau nên \(20cm - 15cm < OO' < 20cm + 15cm\), suy ra \(5cm < OO' < 35cm\).
Đáp án B
Cho hai tiếp tuyến PA và PB của đường tròn (O) (A, B là hai tiếp điểm). Biết \(\widehat {APB} = 60^\circ \), khi đó \(\widehat {APO}\) bằng
- A.
\(120^\circ \).
- B.
\(60^\circ \).
- C.
\(20^\circ \).
- D.
\(30^\circ \).
Đáp án : D
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
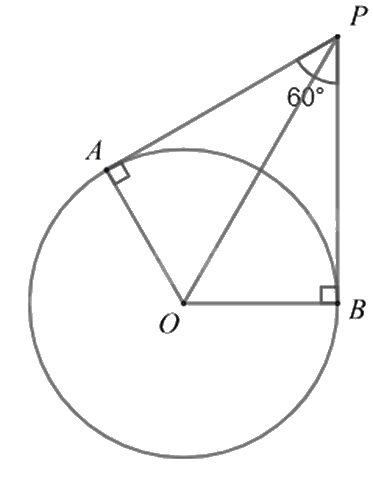
Vì hai tiếp tuyến PA và PB của đường tròn (O) cắt nhau tại P nên PO là tia phân giác của \(\widehat {APB}\), suy ra \(\widehat {APO} = \widehat {BPO} = \frac{1}{2}\widehat {APB} = \frac{1}{2}.60^\circ = 30^\circ \).
Đáp án D
Cho biểu thức \(A = \left( {\frac{1}{{\sqrt a + 1}} - \frac{1}{{\sqrt a + a}}} \right):\frac{{\sqrt a - 1}}{{2\sqrt a + a + 1}}\) \(\left( {a > 0;a \ne 1} \right)\).
a) \(A = \frac{{\sqrt a + 1}}{{\sqrt a }}\).
b) Giá trị của A khi \(a = 4\) là \(\frac{3}{2}\).
c) Khi \(a \ge 1\) thì \(\sqrt a .A \ge 2\).
d) Có \(0\) giá trị nguyên của \(a\) để \(A\) nguyên.
a) \(A = \frac{{\sqrt a + 1}}{{\sqrt a }}\).
b) Giá trị của A khi \(a = 4\) là \(\frac{3}{2}\).
c) Khi \(a \ge 1\) thì \(\sqrt a .A \ge 2\).
d) Có \(0\) giá trị nguyên của \(a\) để \(A\) nguyên.
a) Sử dụng tính chất của căn thức bậc hai để rút gọn.
b) Thay \(a = 4\) vào A để tính giá trị biểu thức A.
c) Sử dụng tính chất của bất đẳng thức để tính.
d) Đưa A về dạng \(A = a + \frac{b}{c}\) với a, b là các số nguyên, c là biểu thức chứa x.
a) Đúng
Ta có:
\(\begin{array}{l}A = \left( {\frac{1}{{\sqrt a + 1}} - \frac{1}{{\sqrt a + a}}} \right):\frac{{\sqrt a - 1}}{{2\sqrt a + a + 1}}\\A = \left[ {\frac{{\sqrt a }}{{\sqrt a \left( {\sqrt a + 1} \right)}} - \frac{1}{{\sqrt a \left( {1 + \sqrt a } \right)}}} \right]:\frac{{\sqrt a - 1}}{{{{\left( {\sqrt a + 1} \right)}^2}}}\\A = \frac{{\sqrt a - 1}}{{\sqrt a \left( {\sqrt a + 1} \right)}}.\frac{{{{\left( {\sqrt a + 1} \right)}^2}}}{{\sqrt a - 1}}\\A = \frac{{\sqrt a + 1}}{{\sqrt a }}\end{array}\)
b) Đúng
Thay \(a = 4\) vào A, ta được: \(A = \frac{{\sqrt 4 + 1}}{{\sqrt 4 }} = \frac{3}{2}\).
c) Sai
Ta có: \(\sqrt a .A = \sqrt a .\frac{{\sqrt a + 1}}{{\sqrt a }} = \sqrt a + 1\).
Vì \(\sqrt a .A \ge 2\) nên \(\sqrt a + 1 \ge 2\), suy ra \(\sqrt a \ge 1\), do đó \(a \ge 1\).
Kết hợp với điều kiện \(a \ne 1\), ta có \(a > 1\).
d) Đúng
Ta có: \(A = \frac{{\sqrt a + 1}}{{\sqrt a }} = 1 + \frac{1}{{\sqrt a }}\).
Để A nguyên thì \(A = 1 + \frac{1}{{\sqrt a }}\) nguyên, do đó \(\frac{1}{{\sqrt a }}\) nguyên.
Để \(\frac{1}{{\sqrt a }}\) nguyên thì \(\sqrt a \) là ước của 1, và \(\sqrt a > 0\) nên \(\sqrt a = 1\). Suy ra \(a = 1\).
Mà \(a \ne 1\) nên không có giá trị của a để \(A\) nguyên.
Đáp án a) Đ, b) Đ, c) S, d) Đ
Một trường trung học mua \(878\) quyển vở bao gồm \(x\) quyển vở loại thứ nhất và \(y\) quyển vở loại thứ hai (\(x,y \in \mathbb{N}\)). Giá bán mỗi quyển vở loại thứ nhất và loại thứ hai lần lượt là \(7500\) và \(12600\) đồng. Biết tổng số tiền nhà trường đã dùng để mua \(878\) quyển vở là \(9073800\) đồng. Mỗi học sinh xuất sắc được thưởng \(3\) quyển vở loại thứ nhất và \(4\) quyển vở loại thứ hai. Mỗi học sinh giỏi được thưởng \(2\) quyển vở loại thứ nhất và \(2\) quyển vở loại thứ hai, các học sinh khác không được thưởng, tổng số học sinh giỏi và xuất sắc chiếm \(20\% \) số học sinh toàn trường.
a) \(x + y = 878\).
b) \(75x + 126y = 9073800\).
c) \(x = 391\), \(y = 488\).
d) Tổng số học sinh của trường là \(749\).
a) \(x + y = 878\).
b) \(75x + 126y = 9073800\).
c) \(x = 391\), \(y = 488\).
d) Tổng số học sinh của trường là \(749\).
Dựa vào đề bài để lập hai phương trình bậc nhất hai ẩn.
Từ đó giải hệ được tạo thành bởi hai phương trình vừa lập.
Tính số học sinh giỏi và xuất sắc, từ đó tính số học sinh toàn trường.
a) Đúng
Vì trường trung học mua \(878\) quyển vở bao gồm \(x\) quyển vở loại thứ nhất và \(y\) quyển vở loại thứ hai nên ta có: \(x + y = 878\).
b) Sai
Vì giá bán mỗi quyển vở loại thứ nhất và loại thứ hai lần lượt là \(7500\) và \(12600\) đồng và tổng số tiền nhà trường đã dùng để mua \(878\) quyển vở là \(9073800\) đồng nên ta có phương trình: \(7500x + 12600y = 9\,073\,800\)
Suy ra \(75x + 126y = 90\,738\).
c) Sai
Hệ phương trình là: \(\left\{ \begin{array}{l}x + y = 878\\75x + 126y = 90\,738\end{array} \right.\).
Giải hệ phương trình:
\(\begin{array}{l}\left\{ \begin{array}{l}x + y = 878\\75x + 126y = 90\,738\end{array} \right.\\\left\{ \begin{array}{l}y = 878 - x\\75x + 126\left( {878 - x} \right) = 90\,738\end{array} \right.\\\left\{ \begin{array}{l}y = 878 - x\\ - 51x = - 19\,890\end{array} \right.\\\left\{ \begin{array}{l}x = 390\\y = 878 - 390\end{array} \right.\\\left\{ \begin{array}{l}x = 390\\y = 488\end{array} \right.\end{array}\)
Vậy \(x = 390;y = 488\).
d) Sai
Gọi số học sinh xuất sắc là a, số học sinh giỏi là b (học sinh, \(a,b \in {\mathbb{N}^*}\))
Vì học sinh xuất sắc được thưởng \(3\) quyển vở loại thứ nhất, mỗi học sinh giỏi được thưởng 2 quyển vở loại thứ nhất nên ta có: \(3a + 2b = 390\).
Vì học sinh xuất sắc được thưởng \(4\) quyển vở loại thứ hai, mỗi học sinh giỏi được thưởng \(2\) quyển vở loại thứ hai nên ta có: \(4a + 2b = 488\).
Ta có hệ phương trình:
\(\left\{ \begin{array}{l}3a + 2b = 390\\4a + 2b = 488\end{array} \right.\)
\(\begin{array}{l}\left\{ \begin{array}{l}a = 98\\3.98 + 2b = 390\end{array} \right.\\\left\{ \begin{array}{l}a = 98\\b = 48\end{array} \right.\end{array}\)
Tổng số học sinh giỏi và xuất sắc là: \(98 + 48 = 146\)
Vì tổng số học sinh giỏi và xuất sắc chiếm \(20\% \) số học sinh toàn trường nên số học sinh của trường là:
\(146:20\% = 730\)
Vậy tổng số học sinh của trường là \(730\).
Đáp án a) Đ, b) S, c) S, d) S
Một trường trung học dự định tổ chức chuyến tham quan học tập thực tế cho học sinh khối 9 tại một bảo tàng và công viên khoa học (Science Park) trong 1 ngày (trong ngày từ 7h00 đến 17h00). Tổng kinh phí nhà trường dự trù là 20 triệu đồng, bao gồm chi phí thuê xe đưa đón và bữa ăn cho học sinh. Gọi \(x\) là số bạn có thể tham gia chuyến tham quan. (học sinh, \(x > 0\))
• Giá thuê xe là 5 triệu đồng/ngày.
• Vé vào cổng mỗi học sinh là 30 000 đồng.
• Bữa ăn trưa cho mỗi học sinh có giá 50 000 đồng.
a) Chi phí cho mỗi học sinh là 80 000 đồng.
b) Tổng chi phí nhà trường cần trả cho chuyến tham quan có \(x\) bạn là \(80\,000x\).
c) \(80\,000x + 5\,000\,000 \le 20\,000\,000\).
d) Trường có thể tổ chức cho tối đa 188 học sinh tham gia chuyến tham quan này.
a) Chi phí cho mỗi học sinh là 80 000 đồng.
b) Tổng chi phí nhà trường cần trả cho chuyến tham quan có \(x\) bạn là \(80\,000x\).
c) \(80\,000x + 5\,000\,000 \le 20\,000\,000\).
d) Trường có thể tổ chức cho tối đa 188 học sinh tham gia chuyến tham quan này.
Vì chuyến tham quan từ 7h00 đến 17h00, mỗi học sinh sẽ có chi phí vé vào cổng và bữa ăn trưa nên ta cần tính chi phí cho một học sinh đi tham quan.
Tổng chi phí nhà trường phải trả bao gồm chi phí cho \(x\) học sinh tham gia và chi phí thuê xe một ngày.
Vì tổng kinh phí nhà trường dự trù là 20 triệu đồng nên tổng chi phí không được quá 20 triệu đồng. Từ đó ta lập được bất phương trình.
Giải bất phương trình để tìm x.
a) Đúng
Vì chuyến tham quan từ 7h00 đến 17h00, mỗi học sinh sẽ có chi phí vé vào cổng và bữa ăn trưa nên chi phí cho một học sinh đi tham quan là:
30 000 + 50 000 = 80 000 (đồng)
b) Sai
Tổng chi phí nhà trường phải trả bao gồm chi phí cho \(x\) học sinh tham gia và chi phí thuê xe một ngày là:
80 000\(x\)+ 5 000 000 (đồng)
c) Đúng
Vì tổng kinh phí nhà trường dự trù là 20 triệu đồng nên ta có bất phương trình:
\(80\,000x + 5\,000\,000 \le 20\,000\,000\)
d) Sai
Giải bất phương trình:
\(80\,000x + 5\,000\,000 \le 20\,000\,000\)
\(80\,000x \le 15\,000\,000\) (cộng cả hai vế với \( - 5\,000\,000\))
\(x \le \frac{{15\,000\,000}}{{8\,000\,000}}\) (nhân cả hai vế với \(\frac{1}{{80\,000}}\))
\(x \le 187,5\)
Vì số học sinh phải là số nguyên nên số học sinh tối đa là 187.
Trường có thể tổ chức cho tối đa 187 học sinh tham gia chuyến tham quan này.
Đáp án a) Đ, b) S, c) Đ, d) S.
Cho tam giác MNP có MN = 5cm, NP = 12cm, MP = 13cm. Vẽ đường tròn \(\left( {M;MN} \right)\), gọi Q là giao điểm của đường tròn với MP.
a) NP là tiếp tuyến của \(\left( {M;MN} \right)\).
b) \(\widehat {NPM} \approx 30^\circ \).
c) sđ$\overset\frown{NQ}\approx 67{}^\circ $.
d) \(\widehat {PNQ} \approx 35^\circ \).
a) NP là tiếp tuyến của \(\left( {M;MN} \right)\).
b) \(\widehat {NPM} \approx 30^\circ \).
c) sđ$\overset\frown{NQ}\approx 67{}^\circ $.
d) \(\widehat {PNQ} \approx 35^\circ \).
a) Chứng minh tam giác MNP vuông dựa vào định lí Pythagore đảo.
b) Sử dụng hệ thức lượng trong tam giác vuông để tính góc NPM.
b) Tính số đo góc ở tâm NMP, từ đó suy ra số đo cung nhỏ NP.
d) Tam giác MNQ cân nên ta tính được \(\widehat {MNQ}\), sử dụng tính chất hai góc phụ nhau để suy ra \(\widehat {PNQ}\).
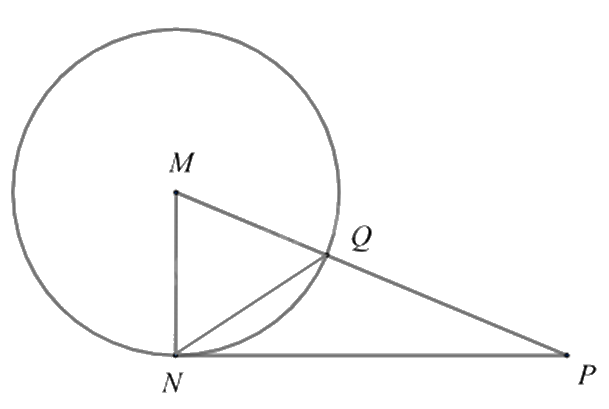
a) Đúng
Xét tam giác MNP có:
\({13^2} = {12^2} + {5^2}\) hay \(M{P^2} = M{N^2} + N{P^2}\)
Suy ra tam giác MNP là tam giác vuông tại N (theo định lí Pythagore đảo)
Suy ra \(MN \bot NP\) và \(N \in \left( {M;MN} \right)\) nên NP là tiếp tuyến của \(\left( {M;MN} \right)\).
b) Sai
Áp dụng hệ thức lượng trong tam giác vuông MNP, ta có:
\(\sin NPM = \frac{{MN}}{{MP}} = \frac{5}{{13}}\) suy ra \(\widehat {NPM} \approx 23^\circ \).
c) Đúng
Ta có: \(\widehat {NMP} = 90^\circ - \widehat {NPM} \approx 90^\circ - 23^\circ = 67^\circ \).
Vì \(\widehat {NMP}\) là góc ở tâm khác góc bẹt nên $\overset\frown{NQ}$ là cung nhỏ, do đó sđ$\overset\frown{NQ}=\widehat{NMQ}\approx 67{}^\circ $.
d) SaiTam giác NMQ cân tại M (MN = MQ = bán kính) nên \(\widehat {MNQ} = \widehat {MQN} = \frac{{180^\circ - \widehat {NMQ}}}{2} \approx \frac{{180^\circ - 67^\circ }}{2} \approx 57^\circ \).
Suy ra \(\widehat {PNQ} = 90^\circ - \widehat {MNQ} \approx 90^\circ - 57^\circ = 33^\circ \).
Đáp án a) Đ, b) S, c) Đ, d) S
Phương trình \(x\left( {x - 5} \right) + 2\left( {x - 5} \right) = 0\) có tổng hai nghiệm bằng:
Đáp án:
Đáp án:
Đưa phương trình về phương trình tích. Giải phương trình tích rồi tính tổng hai nghiệm.
Ta có:
\(\begin{array}{l}x\left( {x - 5} \right) + 2\left( {x - 5} \right) = 0\\\left( {x + 2} \right)\left( {x - 5} \right) = 0\end{array}\)
\(x + 2 = 0\) suy ra \(x = - 2\).
\(x - 5 = 0\) suy ra \(x = 5\).
Suy ra tổng hai nghiệm là \( - 2 + 5 = 3\).
Đáp án: 3
Giá trị của biểu thức \(\sqrt {\frac{3}{5}} - \sqrt {\frac{5}{3}} + \frac{{\sqrt {60} }}{{15}}\) có kết quả bằng:
Đáp án:
Đáp án:
Sử dụng kiến thức của căn bậc hai để tính giá trị biểu thức.
Ta có:
\(\begin{array}{l}\sqrt {\frac{3}{5}} - \sqrt {\frac{5}{3}} + \frac{{\sqrt {60} }}{{15}}\\ = \frac{{\sqrt {3.5} }}{5} - \frac{{\sqrt {5.3} }}{3} + \frac{{\sqrt {4.15} }}{{15}}\\ = \frac{{\sqrt {15} }}{5} - \frac{{\sqrt {15} }}{3} + \frac{{2\sqrt {15} }}{{15}}\\ = \frac{{3\sqrt {15} }}{{15}} - \frac{{5\sqrt {15} }}{{15}} + \frac{{2\sqrt {15} }}{{15}}\\ = \frac{{3\sqrt {15} - 5\sqrt {15} + 2\sqrt {15} }}{{15}}\\ = 0\end{array}\)
Đáp án: 0
Tổng các giá trị của x để \(\sqrt {{x^2} - 6x + 9} = 2\) là:
Đáp án:
Đáp án:
Sử dụng kiến thức \(\sqrt {{A^2}} = \left| A \right|\), giải phương trình để tìm x.
Ta có:
\(\begin{array}{l}\sqrt {{x^2} - 6x + 9} = 2\\\sqrt {{{\left( {x - 3} \right)}^2}} = 2\\\left| {x - 3} \right| = 2\end{array}\)
Suy ra \(x - 3 = 2\) hoặc \(x - 3 = - 2\).
+) Với \(x - 3 = 2\) suy ra \(x = 5\).
+) Với \(x - 3 = - 2\) suy ra \(x = 1\).
Vậy tổng các giá trị của x là: \(5 + 1 = 6\).
Đáp án: 6
Cho hai đường tròn \(\left( {A;3cm} \right)\) và \(\left( {B;5cm} \right)\) đựng nhau. Gọi M, N lần lượt là giao điểm của AB với \(\left( {A;3cm} \right)\). Gọi C, D lần lượt là giao điểm của AB với \(\left( {B;5cm} \right)\) sao cho C, M nằm cùng phía đối với A còn N, D nằm cùng phía đối với B. Tổng ND + CM là bao nhiêu cm?
Đáp án:
Đáp án:
Dựa vào vị trí của các điểm để tính độ dài các đoạn thẳng.
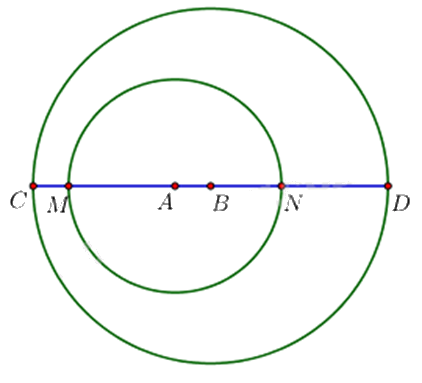
Ta có:
\(CM = BC - AM - AB\)
\(ND = BD - BN = BD - \left( {AN - AB} \right) = BD - AN + AB\)
Suy ra \(CM + ND = BC - AM - AB + \left( {BD - AN + AB} \right)\)
\(\begin{array}{l} = BC - AM - AB + BD - AN + AB\\ = BC + BD - \left( {AM + AN} \right)\end{array}\)
Mà \(BC = BD = 5cm,AM = AN = 3cm\)
Suy ra \(CM + ND = 2.5 - 2.3 = 4\left( {cm} \right)\)
Đáp án: 4
Một đầu của cần gạt nước được cố định tại điểm O. Khi đầu còn lại của cần gạt xoay \(60^\circ \), nó sẽ quét được một vùng có diện tích bằng \(\frac{8}{3}\pi \left( {{m^2}} \right)\).
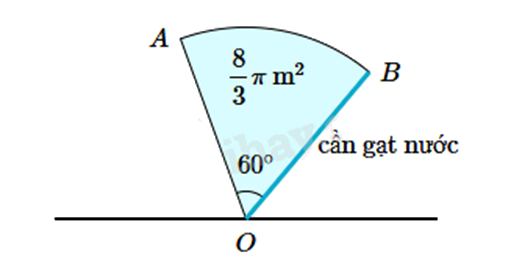
Chiều dài của cần gạt nước là bao nhiêu m?
Đáp án:
Đáp án:
Dựa vào công thức tính diện tích hình quạt tròn: \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Vì diện tích hình quạt tròn là \(\frac{8}{3}\pi \) nên ta có: \(\frac{{\pi .{R^2}.60}}{{360}} = \frac{{\pi {R^2}}}{6} = \frac{8}{3}\pi \).
Suy ra \({R^2} = \frac{8}{3}\pi :\frac{\pi }{6} = 16\).
Do đó \(R = \sqrt {16} = 4\left( m \right)\).
Vậy chiều dài của cần gạt nước là 4m.
Đáp án: 4
Cho \(\alpha \) là góc nhọn bất kì. Khi đó \(C = {\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha .{\cos ^2}\alpha \) có giá trị bằng:
Đáp án:
Đáp án:
Sử dụng công thức mở rộng \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
\(\begin{array}{l}C = {\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha .{\cos ^2}\alpha \\C = {\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha .{\cos ^2}\alpha .1\\C = {\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha .{\cos ^2}\alpha \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\\C = {\left( {{{\sin }^2}\alpha } \right)^3} + {\left( {{{\cos }^2}\alpha } \right)^3} + 3{\sin ^4}\alpha .{\cos ^2}\alpha + 3{\sin ^2}\alpha .{\cos ^4}\alpha \\C = {\left( {{{\sin }^2}\alpha } \right)^3} + 3{\sin ^4}\alpha .{\cos ^2}\alpha + 3{\sin ^2}\alpha .{\cos ^4}\alpha + {\left( {{{\cos }^2}\alpha } \right)^3}\\C = {\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)^3} = {1^3} = 1\end{array}\)
Đáp án: 1
Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 5: Tổng quan và Hướng dẫn Ôn tập
Học kì 1 Toán 9 là giai đoạn quan trọng, đặt nền móng cho việc học Toán ở các lớp trên. Việc làm quen với các dạng đề thi và luyện tập thường xuyên là chìa khóa để đạt kết quả tốt. Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 5 của tusach.vn được thiết kế để hỗ trợ học sinh trong quá trình ôn tập này.
Cấu trúc Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 5
Đề thi này bao gồm các phần chính sau:
- Phần trắc nghiệm: Kiểm tra kiến thức cơ bản và khả năng vận dụng nhanh các công thức, định lý.
- Phần tự luận: Đòi hỏi học sinh trình bày chi tiết các bước giải, thể hiện khả năng phân tích và suy luận logic.
Các chủ đề chính được đề cập trong đề thi bao gồm:
- Đại số: Biểu thức đại số, phương trình bậc nhất một ẩn, hệ phương trình bậc nhất hai ẩn.
- Hình học: Hệ thức lượng trong tam giác vuông, hàm số bậc nhất, đồ thị hàm số.
Tại sao nên luyện tập với Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 5?
Có rất nhiều lý do để bạn nên sử dụng đề thi này trong quá trình ôn tập:
- Bám sát chương trình: Đề thi được biên soạn theo chương trình học chính thức của Bộ Giáo dục và Đào tạo.
- Đa dạng dạng bài: Đề thi bao gồm nhiều dạng bài tập khác nhau, giúp bạn làm quen với các tình huống có thể xuất hiện trong đề thi thật.
- Đáp án chi tiết: Đáp án đi kèm với đề thi giúp bạn tự kiểm tra và đánh giá kết quả học tập, đồng thời hiểu rõ cách giải các bài toán.
- Miễn phí: Đề thi được cung cấp miễn phí trên tusach.vn, giúp bạn tiết kiệm chi phí ôn tập.
Hướng dẫn ôn tập hiệu quả cho Đề thi học kì 1 Toán 9 Kết nối tri thức
Để đạt kết quả tốt nhất trong kỳ thi học kì 1, bạn nên:
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các công thức, định lý và ví dụ minh họa.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau, từ dễ đến khó, để rèn luyện kỹ năng giải toán.
- Sử dụng đề thi thử: Làm các đề thi thử để làm quen với cấu trúc đề thi và thời gian làm bài.
- Hỏi thầy cô giáo: Nếu gặp khó khăn trong quá trình học tập, hãy hỏi thầy cô giáo để được giải đáp.
Tải Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 5 ngay hôm nay!
Đừng bỏ lỡ cơ hội ôn tập hiệu quả với Đề thi học kì 1 Toán 9 Kết nối tri thức - Đề số 5 của tusach.vn. Hãy tải đề thi ngay hôm nay và bắt đầu luyện tập để đạt kết quả tốt nhất trong kỳ thi sắp tới!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Biểu thức đại số | Cao |
| Phương trình bậc nhất một ẩn | Cao |
| Hệ phương trình bậc nhất hai ẩn | Trung bình |
| Hệ thức lượng trong tam giác vuông | Cao |
| Hàm số bậc nhất | Trung bình |
| Nguồn: tusach.vn | |