Đề thi giữa kì 2 Toán 9 - Đề số 4
Tổng quan nội dung
Đề thi giữa kì 2 Toán 9 - Đề số 4
Chào mừng các em học sinh lớp 9 đến với đề thi giữa kì 2 Toán 9 - Đề số 4 do tusach.vn biên soạn.
Đề thi này được thiết kế bám sát chương trình học, giúp các em làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải toán.
Cùng tusach.vn ôn tập và chuẩn bị tốt nhất cho kỳ thi sắp tới!
Đề bài
Cho hàm số \(y = {x^2}\). Với \(y = 4\) thì giá trị của \(x\) bằng
- A.
8 và -8.
- B.
4 và -4.
- C.
2 và -2.
- D.
2.
Cho phương trình \({x^2} - 2x - m + 1 = 0\) có nghiệm \({x_1} = - 1\). Giá trị của tham số m là:
- A.
4.
- B.
-4.
- C.
2.
- D.
-2.
Biết rằng \({x^2} - 5x + 2 = 0\) có hai nghiệm \({x_1};{x_2}\). Khi đó \({x_1}^2 + {x_2}^2\) bằng
- A.
20.
- B.
21.
- C.
22.
- D.
23.
Cho bảng tần số - tần số tương đối điểm kiểm tra của lớp 9B như sau:

Tần số tương đối của điểm 8 là bao nhiêu?
- A.
7%.
- B.
12,5%.
- C.
20%.
- D.
17,5%.
Tính bán kính đường tròn nội tiếp của tam giác đều có cạnh bằng 16cm.
- A.
\(4\sqrt 3 \)cm.
- B.
\(8\sqrt 3 \)cm.
- C.
\(\frac{{8\sqrt 3 }}{3}\)cm.
- D.
\(\frac{{16\sqrt 3 }}{3}\)cm.
Cho tứ giác \(MNPQ\) nội tiếp đường tròn (O). Biết \(\widehat {MNQ} = 60^\circ ,\widehat {QMP} = 40^\circ \). Số đo góc MQP là
- A.
\(40^\circ \).
- B.
\(25^\circ \).
- C.
\(80^\circ \).
- D.
\(60^\circ \).
Tại một hội nghị khoa học quốc tế năm 2022, ban tổ chức khảo sát số lượng ngôn ngữ mà mỗi đại biểu có thể sử dụng. Kết quả thu được như sau:

a) Bảng tần số tương đối cho dữ liệu trên như sau:

b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là 35%.
c) Biểu đồ tần số tương đối cho dữ liệu trên là:
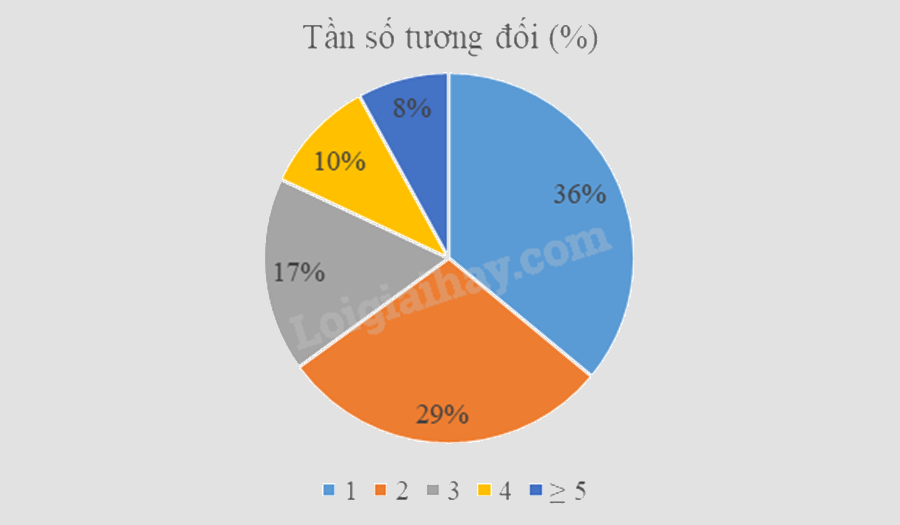
d) Tại hội nghị khoa học quốc tế được tổ chức năm 2023, có 65 trong tổng số 180 đại biểu tham dự có thể sử dụng được từ 3 ngoại ngữ trở lên. Do đó tỉ lệ đại biểu sử dụng được từ 3 ngoại ngữ trở lên năm 2023 tăng so với năm 2022.
Cho tam giác ABC nhọn nội tiếp đường tròn tâm \(\left( O \right)\), đường cao AH, đường kính AM. Gọi I là trung điểm BC.
a) \(\widehat {ACM} = 45^\circ \).
b) \(\widehat {OAC} = \widehat {BAH}\).
c) \(OI{\mkern 1mu} {\rm{//}}{\mkern 1mu} AH\).
d) Gọi N là giao điểm của AH với đường tròn \(\left( O \right)\). Tứ giác BCMN là hình bình hành.
Cho hàm số \(y = \left( {2m + 2} \right){x^2}\). Tìm m để đồ thị hàm số đi qua điểm \(A\left( {x;y} \right)\) với \(\left( {x;y} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x - y = 2\end{array} \right.\).
Đáp án:
Tích các giá trị của m để phương trình \(7m{x^2} - 24x - 4{m^2} = 0\) có nghiệm \(x = 2\).
Đáp án:
Một phường cho trẻ em từ 2 tháng tuổi trở lên tiêm vắc xin 6 in 1. Bảng sau thống kê số mũi vắc xin 6 in 1 mà 60 trẻ em từ 2 tháng tuối đến 24 tháng tuổi của phường này đã tiêm.
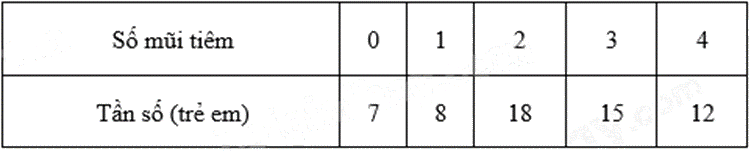
Trẻ em từ 2 tháng tuổi đến 24 tháng tuổi cần hoàn thành 4 mũi tiêm của vắc xin 6 in 1. Hỏi có bao nhiêu trẻ em của phường trên cần phải hoàn thành lộ trình tiêm vắc xin này?
Đáp án:
Cho tam giác ABC có CK và BD là hai đường cao. Biết \(\widehat {ACB} = 50^\circ \), số đo \(\widehat {AKD}\) bằng … (không cần ghi độ)
Đáp án:
Lúc \(7\) giờ một ô tô đi từ A đến B. Lúc \(7\) giờ 30 phút một xe máy đi từ B đến A với vận tốc kém vận tốc của ô tô là \(24\left( {{\rm{km/h}}} \right)\). Ô tô đến B được 20 phút thì xe máy mới đến \(A\). Tính vận tốc mỗi xe, biết quãng đường AB dài \(120\left( {{\rm{km}}} \right)\).
Cho \(\Delta ABC\) nhọn có \(\widehat {BAC} = 60^\circ \). Vẽ đường tròn đường kính BC tâm \(O\) cắt AB, AC lần lượt tại \(D\) và \(E\).
a) Tính số đo $\overset\frown{DE}$.
b) Tia DO cắt đường tròn tại \(K\). Tính góc EDK.
Cho phương trình \({x^2} - 2x + m - 3 = 0\)(m là tham số)
Tìm m để phương trình có hai nghiệm \({x_1};{x_2}\) sao cho biểu thức \(P = {x_1}^2 + {x_2}^2 + {\left( {{x_1}{x_2}} \right)^2}\) đạt giá trị nhỏ nhất.
Lời giải và đáp án
Cho hàm số \(y = {x^2}\). Với \(y = 4\) thì giá trị của \(x\) bằng
- A.
8 và -8.
- B.
4 và -4.
- C.
2 và -2.
- D.
2.
Đáp án : C
Thay \(y = 4\) vào hàm số, ta tính được giá trị của \(x\) tương ứng.
Thay \(y = 4\) vào hàm số \(y = {x^2}\) ta được \(4 = {x^2}\) suy ra \(x = 2\) hoặc \(x = - 2\)
Vậy \(x = 2\) và \(x = - 2\).
Đáp án C
Cho phương trình \({x^2} - 2x - m + 1 = 0\) có nghiệm \({x_1} = - 1\). Giá trị của tham số m là:
- A.
4.
- B.
-4.
- C.
2.
- D.
-2.
Đáp án : A
Thay nghiệm \({x_1}\) vào phương trình để tìm m.
Thay \({x_1} = - 1\) vào phương trình \({x^2} - 2x - m + 1 = 0\), ta được:
\(\begin{array}{l}{\left( { - 1} \right)^2} - 2.\left( { - 1} \right) - m + 1 = 0\\1 + 2 - m + 1 = 0\\m = 4\end{array}\)
Vậy m = 4.
Đáp án A
Biết rằng \({x^2} - 5x + 2 = 0\) có hai nghiệm \({x_1};{x_2}\). Khi đó \({x_1}^2 + {x_2}^2\) bằng
- A.
20.
- B.
21.
- C.
22.
- D.
23.
Đáp án : B
- Kiểm tra số nghiệm của phương trình \(a{x^2} + bx + c = 0\) bằng \(\Delta \): \(\Delta = {b^2} - 4ac\).
- Sử dụng định lí Viète để tìm \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}{x_2} = \frac{c}{a}\end{array} \right.\).
- Biến đổi \({x_1}^2 + {x_2}^2\) theo \({x_1} + {x_2};{x_1}{x_2}\).
Ta có: \(\Delta = {\left( { - 5} \right)^2} - 4.2 = 17 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1};{x_2}\).
Theo định lí Viète, ta có:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}{x_2} = 2\end{array} \right.\)Khi đó:
\(\begin{array}{l}{x_1}^2 + {x_2}^2\\ = \left( {{x_1}^2 + 2{x_1}{x_2} + {x_2}^2} \right) - 2{x_1}{x_2}\\ = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\\ = {5^2} - 2.2\\ = 25 - 4\\ = 21\end{array}\)
Đáp án B
Cho bảng tần số - tần số tương đối điểm kiểm tra của lớp 9B như sau:

Tần số tương đối của điểm 8 là bao nhiêu?
- A.
7%.
- B.
12,5%.
- C.
20%.
- D.
17,5%.
Đáp án : D
Quan sát bảng tần số - tần số tương đối để xác định tần số tương đối của điểm 8.
Tần số tương đối của điểm 8 là 17,5%.
Đáp án D
Tính bán kính đường tròn nội tiếp của tam giác đều có cạnh bằng 16cm.
- A.
\(4\sqrt 3 \)cm.
- B.
\(8\sqrt 3 \)cm.
- C.
\(\frac{{8\sqrt 3 }}{3}\)cm.
- D.
\(\frac{{16\sqrt 3 }}{3}\)cm.
Đáp án : C
Sử dụng công thức tính bán kính đường tròn nội tiếp tam giác đều cạnh a: \(r = \frac{{\sqrt 3 }}{6}a\).
Bán kính đường tròn nội tiếp của tam giác đều cạnh bằng 16cm là: \(r = \frac{{\sqrt 3 }}{6} \cdot 16 = \frac{{8\sqrt 3 }}{3}\)cm
Đáp án C
Cho tứ giác \(MNPQ\) nội tiếp đường tròn (O). Biết \(\widehat {MNQ} = 60^\circ ,\widehat {QMP} = 40^\circ \). Số đo góc MQP là
- A.
\(40^\circ \).
- B.
\(25^\circ \).
- C.
\(80^\circ \).
- D.
\(60^\circ \).
Đáp án : C
Dựa vào hai góc nội tiếp cùng chắn một cung để tính \(\widehat {QNP}\), suy ra \(\widehat {MNP}\).
Từ định lí tổng hai góc đối của tứ giác nội tiếp, tính \(\widehat {MQP}\).
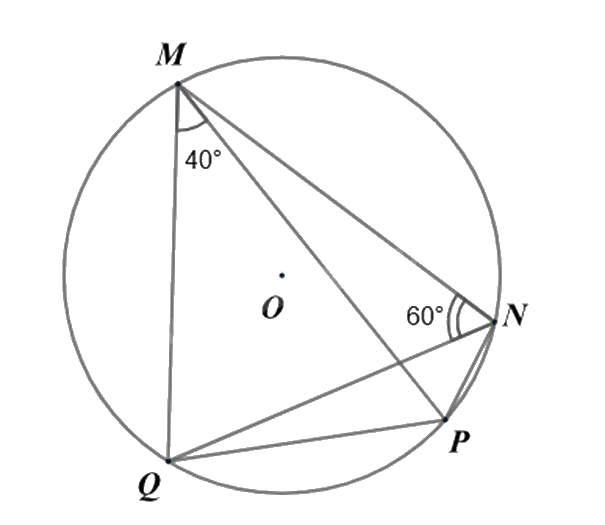
Vì tứ giác MNPQ nội tiếp đường tròn (O) nên \(\widehat {QMP} = \widehat {QNP}\) (hai góc nội tiếp chắn cung PQ), suy ra \(\widehat {QNP} = 40^\circ \).
Ta có: \(\widehat {MNP} = \widehat {MPQ} + \widehat {QNP} = 60^\circ + 40^\circ = 100^\circ \).
Áp dụng định lí tổng hai góc đối của tứ giác nội tiếp, ta có: \(\widehat {MQP} + \widehat {MNP} = 180^\circ \)
Suy ra \(\widehat {MQP} = 180^\circ - \widehat {MNP} = 180^\circ - 100^\circ = 80^\circ \).
Đáp án C
Tại một hội nghị khoa học quốc tế năm 2022, ban tổ chức khảo sát số lượng ngôn ngữ mà mỗi đại biểu có thể sử dụng. Kết quả thu được như sau:

a) Bảng tần số tương đối cho dữ liệu trên như sau:

b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là 35%.
c) Biểu đồ tần số tương đối cho dữ liệu trên là:
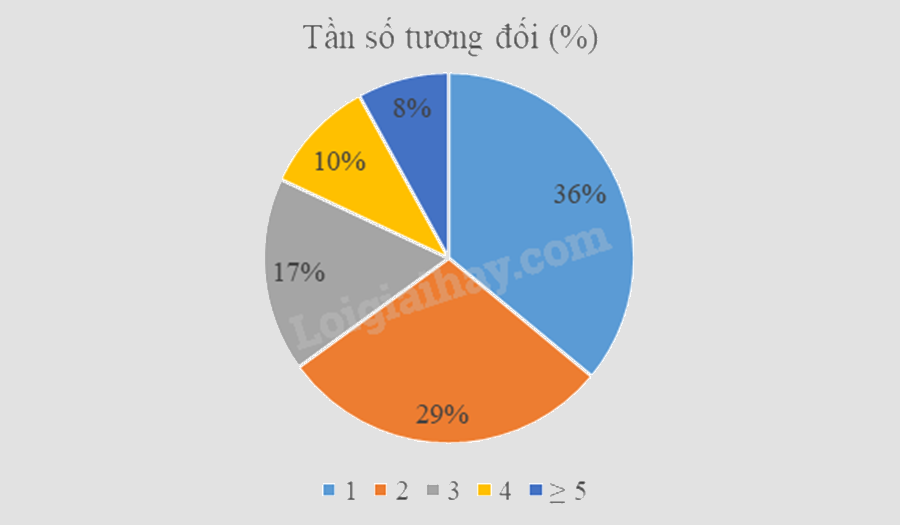
d) Tại hội nghị khoa học quốc tế được tổ chức năm 2023, có 65 trong tổng số 180 đại biểu tham dự có thể sử dụng được từ 3 ngoại ngữ trở lên. Do đó tỉ lệ đại biểu sử dụng được từ 3 ngoại ngữ trở lên năm 2023 tăng so với năm 2022.
a) Bảng tần số tương đối cho dữ liệu trên như sau:

b) Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là 35%.
c) Biểu đồ tần số tương đối cho dữ liệu trên là:
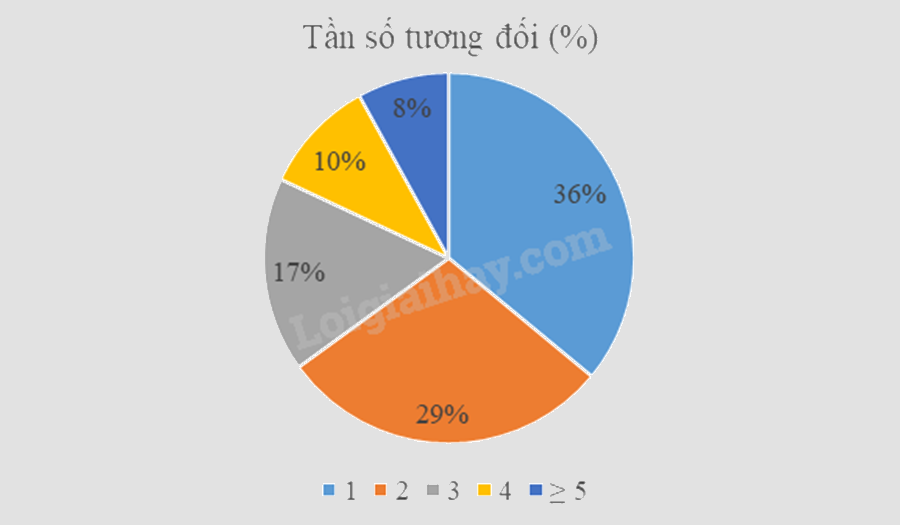
d) Tại hội nghị khoa học quốc tế được tổ chức năm 2023, có 65 trong tổng số 180 đại biểu tham dự có thể sử dụng được từ 3 ngoại ngữ trở lên. Do đó tỉ lệ đại biểu sử dụng được từ 3 ngoại ngữ trở lên năm 2023 tăng so với năm 2022.
a) Sử dụng công thức tính tần số tương đối cho dữ liệu: \(f = \frac{m}{N}.100\% \), trong đó m là tần số của giá trị và N là cỡ mẫu. Sau đó lập bảng tần số tương đối.
b) Tính tổng tần số tương đối của các đại biểu sử dụng được ít nhất 2 ngoại ngữ.
c) Từ bảng tần số tương đối đã lập để vẽ biểu đồ tần số tương đối phù hợp.
Công thức đổi từ tần số tương đối sang độ: \(360^\circ .{f_i}\).
d) Tính tần số tương đối của số đại biểu sử dụng được từ 3 ngoại ngữ trở nên trong năm 2022 và 2023.
So sánh hai tần số tương đối với của số đại biểu sử dụng được từ 3 ngoại ngữ trong hai năm với nhau.
a) Sai
Tổng số đại biểu là: \(72 + 58 + 34 + 20 + 16 = 200\)
Tần số tương đối của các giá trị 1; 2; 3; 4; \( \ge \)5 lần lượt là:
\(\begin{array}{l}\frac{{72}}{{200}}.100\% = 36\% ;\frac{{58}}{{200}}.100\% = 29\% ;\frac{{34}}{{200}}.100\% = 17\% ;\\\frac{{20}}{{200}}.100\% = 10\% ;\frac{{16}}{{200}}.100\% = 8\% \end{array}\)
Vậy bảng tần số tương đối cho dữ liệu trên như sau:

b) Sai
Tỉ lệ phần trăm đại biểu sử dụng được ít nhất 2 ngoại ngữ là:
\(29 + 17 + 10 + 8 = 64\left( \% \right)\).
c) Đúng
Từ bảng tần số tương đối, ta có số độ tương ứng với các giá trị tần số là:
\(\begin{array}{l}360^\circ .36\% \approx 130^\circ ;360^\circ .29\% \approx 104^\circ ;360^\circ .17\% \approx 61^\circ ;\\360^\circ .10\% = 36^\circ ;360^\circ .8\% = 29^\circ \end{array}\)
Vẽ được biểu đồ tần số tương đối:
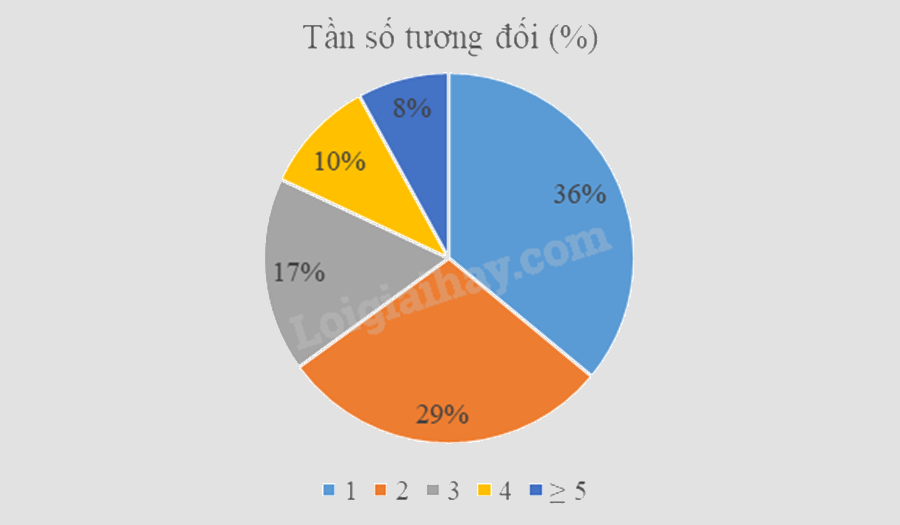
d) Đúng
Tỉ lệ đại biểu sử dụng từ 3 ngôn ngữ trở lên trong hội nghị năm 2022 là: \(17\% + 10\% + 8\% = 35\% \)
Tỉ lệ đại biểu sử dụng từ 3 ngôn ngữ trở lên trong hội nghị năm 2023 là: \(\frac{{65}}{{180}}.100\% \approx 36,1\% \)
Ta thấy 36,1% > 35% nên tỉ lệ đại biểu sử dụng được từ 3 ngoại ngữ trở lên năm 2023 tăng so với năm 2022.
Đáp án: SSĐĐ
Cho tam giác ABC nhọn nội tiếp đường tròn tâm \(\left( O \right)\), đường cao AH, đường kính AM. Gọi I là trung điểm BC.
a) \(\widehat {ACM} = 45^\circ \).
b) \(\widehat {OAC} = \widehat {BAH}\).
c) \(OI{\mkern 1mu} {\rm{//}}{\mkern 1mu} AH\).
d) Gọi N là giao điểm của AH với đường tròn \(\left( O \right)\). Tứ giác BCMN là hình bình hành.
a) \(\widehat {ACM} = 45^\circ \).
b) \(\widehat {OAC} = \widehat {BAH}\).
c) \(OI{\mkern 1mu} {\rm{//}}{\mkern 1mu} AH\).
d) Gọi N là giao điểm của AH với đường tròn \(\left( O \right)\). Tứ giác BCMN là hình bình hành.
a) Sử dụng hai góc nội tiếp chắn nửa đường tròn bằng \(90^\circ \).
b) Sử dụng hai góc nội tiếp chắn cùng một cung thì bằng nhau để chứng minh \(\widehat {ABC} = \widehat {AMC}\).
Kết hợp với tổng hai góc phụ nhau để suy ra \(\widehat {OAC} = \widehat {BAH}\).
c) Chứng minh OI là đường cao nên \(OI \bot BC\), mà \(AH \bot BC\) nên \(AH//OI\).
d) Sử dụng hai góc nội tiếp chắn nửa đường tròn bằng \(90^\circ \).
Chứng minh MN // BC suy ra BCMN là hình thang. Chứng minh hai góc ở đáy \(\widehat {CBN} = \widehat {BCM}\) thông qua hai cung trên cùng một đường tròn gọi là bằng nhau nếu chúng có cùng số đo, suy ra BCMN là hình thang cân.
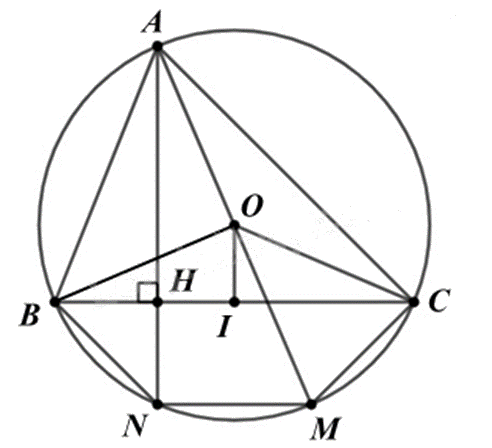
a) Sai
Vì \(\widehat {ACM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACM} = 90^\circ \).
b) Đúng
Xét (O) có: \(\widehat {ABC} = \widehat {AMC}\) (hai góc nội tiếp cùng chắn cung AC).
Mà \(\widehat {BAH} + \widehat {ABC} = 90^\circ \left( {AH \bot BC} \right)\)
Lại có: \(\widehat {OAC} + \widehat {AMC} = 90^\circ \) (tam giác ACM có \(\widehat {ACM} = 90^\circ \)).
Suy ra \(\widehat {BAH} + \widehat {ABC} = \widehat {OAC} + \widehat {AMC}\)
nên \(\widehat {BAH} = \widehat {OAC}\)
c) Đúng
Tam giác BOC cân tại O (OB = OC = R) có I là trung điểm của BC nên OI là đường trung tuyến đồng thời là đường cao.
Suy ra \(OI \bot BC\)
Mà \(AH \bot BC\) nên \(OI//AH\).
d) Sai
Xét (O) có \(\widehat {ANM}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ANM} = 90^\circ \) suy ra \(AN \bot NM\)
Mà \(BC \bot AN\) suy ra \(MN//BC\). Do đó tứ giác BCMN là hình thang. (1)
Ta lại có: \(\widehat {BAN} = \widehat {CAM}\) (vì \(\widehat {BAH} = \widehat {OAC}\))
Do đó: $\overset\frown{BN}=\overset\frown{CM}$
$\overset\frown{BN}+\overset\frown{MN}=\overset\frown{CM}+\overset\frown{MN}$
$\overset\frown{BNM}=\overset\frown{CMN}$
Do đó \(\widehat {BCM} = \widehat {CBN}\) (2)
Từ (1) và (2) suy ra tứ giác BCMN là hình thang cân.
Đáp án: SĐĐS
Cho hàm số \(y = \left( {2m + 2} \right){x^2}\). Tìm m để đồ thị hàm số đi qua điểm \(A\left( {x;y} \right)\) với \(\left( {x;y} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x - y = 2\end{array} \right.\).
Đáp án:
Đáp án:
Xác định tọa độ điểm \(A\left( {x;y} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x - y = 2\end{array} \right.\). (có thể sử dụng máy tính cầm tay đối với câu dạng trắc nghiệm)
Khi đó thay tọa độ điểm A vào hàm số \(y = a{x^2}\) thì \({y_A} = a{x_A}^2\) nên \(a = \frac{{{y_A}}}{{{x_A}^2}}\) với \({x_A} \ne 0\).
Ta tính được nghiệm của hê phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x - y = 2\end{array} \right.\) là \(\left( { - 1; - 4} \right)\).
Khi đó điểm \(A\left( { - 1; - 4} \right)\) thuộc đồ thị hàm số \(y = \left( {2m + 2} \right){x^2}\).
Thay \(x = - 1;y = - 4\) vào \(y = \left( {2m + 2} \right){x^2}\), ta được:
\(\begin{array}{l} - 4 = \left( {2m + 2} \right).{\left( { - 1} \right)^2}\\2m + 2 = \frac{{ - 4}}{{{{\left( { - 1} \right)}^2}}}\\2m + 2 = - 4\\2m = - 6\\m = - 3\end{array}\)
Đáp án: -3
Tích các giá trị của m để phương trình \(7m{x^2} - 24x - 4{m^2} = 0\) có nghiệm \(x = 2\).
Đáp án:
Đáp án:
Thay \(x = 2\) vào phương trình để tìm m.
Đưa phương trình về phương trình tích, sử dụng công thức nghiệm hoặc sử dụng máy tính cầm tay để tìm m.
Thay \(x = 2\) vào phương trình \(7m{x^2} - 24x - 4{m^2} = 0\), ta được:
\(\begin{array}{l}7m{x^2} - 24x - 4{m^2} = 0\\7m{.2^2} - 24.2 - 4{m^2} = 0\\28m - 48 - 4{m^2} = 0\\4{m^2} - 28m + 48 = 0\\{m^2} - 7m + 12 = 0\end{array}\)
Suy ra \({m_1} = 4;{m_2} = 3\)
Vậy tích các giá trị của m là: \(4.3 = 12\).
Đáp án: 12
Một phường cho trẻ em từ 2 tháng tuổi trở lên tiêm vắc xin 6 in 1. Bảng sau thống kê số mũi vắc xin 6 in 1 mà 60 trẻ em từ 2 tháng tuối đến 24 tháng tuổi của phường này đã tiêm.
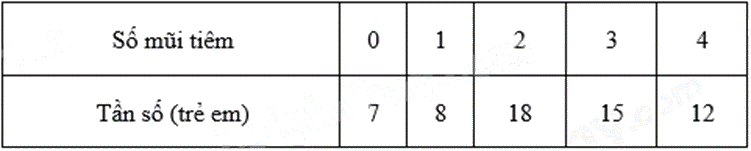
Trẻ em từ 2 tháng tuổi đến 24 tháng tuổi cần hoàn thành 4 mũi tiêm của vắc xin 6 in 1. Hỏi có bao nhiêu trẻ em của phường trên cần phải hoàn thành lộ trình tiêm vắc xin này?
Đáp án:
Đáp án:
Xác định tổng số trẻ em chưa hoàn thành lộ trình tiêm vắc xin dựa vào bảng tần số.
Số trẻ em chưa hoàn thành lộ trình tiêm có số mũi tiêm nhỏ hơn 4.
Vì trẻ em từ 2 tháng tuổi đến 24 tháng tuổi cần hoàn thành 4 mũi tiêm của vắc xin 6 in 1 nên số trẻ em của phường cần phải hoàn thành lộ trình tiêm vắc xin là:
\(7 + 8 + 18 + 15 = 48\) (trẻ em)
Đáp án: 48
Cho tam giác ABC có CK và BD là hai đường cao. Biết \(\widehat {ACB} = 50^\circ \), số đo \(\widehat {AKD}\) bằng … (không cần ghi độ)
Đáp án:
Đáp án:
Chứng minh tứ giác BKDC là tứ giác nội tiếp, suy ra hai góc đối có tổng bằng \(180^\circ \).
Kết hợp với hai góc kề bù có tổng bằng \(180^\circ \).
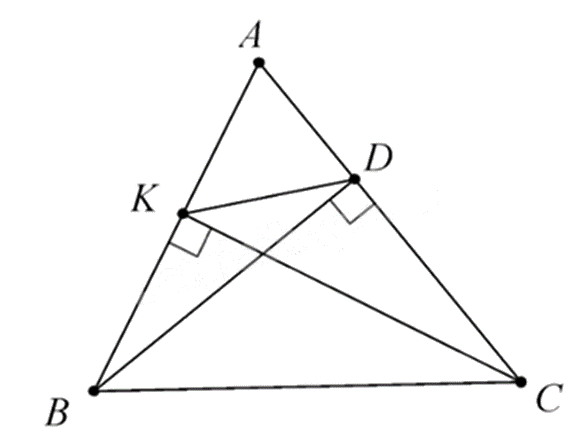
Xét tam giác BKC và tam giác BDC có \(\widehat {BKC} = \widehat {BDC} = 90^\circ \) tam giác BKC và tam giác BDC nội tiếp đường tròn đường kính BC.
Do đó \(B,K,D,C\) thuộc đường tròn đường kính BC hay tứ giác BKDC nội tiếp đường tròn đường kính BC.
Suy ra \(\widehat {BKD} + \widehat {BCD} = 180^\circ \) (định lí tổng hai góc đối của tứ giác nội tiếp)
Mà \(\widehat {BKD} + \widehat {AKD} = 180^\circ \) (hai góc kề bù)
Do đó \(\widehat {BCD} = \widehat {AKD}\) (cùng bù với \(\widehat {BKD}\))
Mà \(\widehat {BCD} = \widehat {BCA} = 50^\circ \) nên \(\widehat {AKD} = 50^\circ \).
Đáp án: 50
Lúc \(7\) giờ một ô tô đi từ A đến B. Lúc \(7\) giờ 30 phút một xe máy đi từ B đến A với vận tốc kém vận tốc của ô tô là \(24\left( {{\rm{km/h}}} \right)\). Ô tô đến B được 20 phút thì xe máy mới đến \(A\). Tính vận tốc mỗi xe, biết quãng đường AB dài \(120\left( {{\rm{km}}} \right)\).
Gọi vận tốc của xe máy là \(x\left( {{\rm{km/h}}} \right)\left( {x > 0} \right)\)
Biểu diễn vận tốc, thời gian xe máy, ô tô đi hết quãng đường.
Lập phương trình dựa vào đề bài.
Giải phương trình, kết hợp điều kiện ban đầu của \(x\).
Gọi vận tốc của xe máy là \(x\left( {{\rm{km/h}}} \right)\left( {x > 0} \right)\)
Vận tốc của ô tô là \(x + 24\left( {{\rm{km/h}}} \right)\)
Thời gian xe máy đi hết quãng đường là: \(\frac{{120}}{x}\)(h)
Thời gian ô tô đi hết quãng đường là: \(\frac{{120}}{{x + 24}}\)(h)
Đổi 30 phút = \(\frac{1}{2}\)(h); 20 phút = \(\frac{1}{3}\)(h)
Theo đề bài ta có phương trình:
\(\begin{array}{l}\frac{{120}}{{x + 24}} + \frac{1}{3} = \frac{{120}}{x} - \frac{1}{2}\\\frac{{120x.3.2}}{{6x\left( {x + 24} \right)}} + \frac{{\left( {x + 24} \right).x.2}}{{6x\left( {x + 24} \right)}} = \frac{{120\left( {x + 24} \right).3.2}}{{6x\left( {x + 24} \right)}} - \frac{{\left( {x + 24} \right).3.x}}{{6x\left( {x + 24} \right)}}\\720x + 2{x^2} + 48x = 720x + 17280 - 3{x^2} - 72x\\5{x^2} + 120x - 17280 = 0\end{array}\)
Giải phương trình, ta được: \({x_1} = 48\left( {t/m} \right);{x_2} = - 72\left( L \right)\)
Vậy vận tốc xe máy là \(48\left( {{\rm{km/h}}} \right)\).
Cho \(\Delta ABC\) nhọn có \(\widehat {BAC} = 60^\circ \). Vẽ đường tròn đường kính BC tâm \(O\) cắt AB, AC lần lượt tại \(D\) và \(E\).
a) Tính số đo $\overset\frown{DE}$.
b) Tia DO cắt đường tròn tại \(K\). Tính góc EDK.
a) Từ góc nội tiếp chắn nửa đường tròn để chứng minh tam giác ADC vuông tại D.
Kết hợp với \(\widehat {BAC} = 60^\circ \) suy ra góc \(\widehat {ECD}\) chắn cung DE.
b) Chứng minh tam giác ODE cân tại O có \(\widehat {DOE} = 60^\circ \) nên tam giác ODE đều.
Suy ra số đo góc EDK
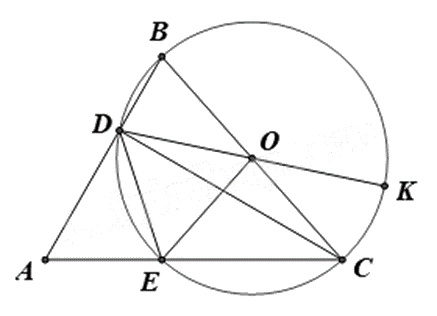
a) Ta có: \(\widehat {BDC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta BDC\) vuông tại D.
Mà \(\widehat A = 60^\circ \) (gt) suy ra \(\widehat {ACD} = 90^\circ - 60^\circ = 30^\circ \) hay \(\widehat {ECD} = 30^\circ \).
Xét đường tròn (O) có \(\widehat {ECD}\) là góc nội tiếp chắn cung DE nên sđ$\overset\frown{DE}=2.\widehat{ECD}=2.30{}^\circ =60{}^\circ $.
b) Vì OD = OE (bán kính đường tròn) nên \(\Delta ODE\) cân tại O.
Mà \(\widehat {DOE} = \)sđ$\overset\frown{DE}$\( = 60^\circ \) (góc ở tâm chắn cung DE)
Suy ra \(\Delta ODE\) đều.
Do đó \(\widehat {EDO} = 60^\circ \) hay \(\widehat {EDK} = 60^\circ \).
Cho phương trình \({x^2} - 2x + m - 3 = 0\)(m là tham số)
Tìm m để phương trình có hai nghiệm \({x_1};{x_2}\) sao cho biểu thức \(P = {x_1}^2 + {x_2}^2 + {\left( {{x_1}{x_2}} \right)^2}\) đạt giá trị nhỏ nhất.
Sử dụng công thức nghiệm \(\Delta = {b^2} - 4ac\), tìm điều kiện của m để \(\Delta \ge 0\)
Sử dụng định lí Viète để tìm \({x_2}\): \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}.{x_2} = \frac{c}{a}\end{array} \right.\)
Thay \({x_1};{x_2}\) vào P để tìm giá trị nhỏ nhất của P.
Ta có: \(\Delta = {\left( { - 2} \right)^2} - 4.\left( {m - 3} \right) = 4 - 4m + 12 = - 4m + 16\)
Để phương trình có hai nghiệm thì \(\Delta \ge 0\) hay \( - 4m + 16 \ge 0\), suy ra \(m \le 4\).
Theo định lí Viète, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - \left( { - 2} \right)}}{1} = 2\\{x_1}.{x_2} = \frac{{m - 3}}{1} = m - 3\end{array} \right.\).
Ta có:
\(\begin{array}{l}P = {x_1}^2 + {x_2}^2 + {\left( {{x_1}{x_2}} \right)^2}\\ = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + {\left( {{x_1}{x_2}} \right)^2}\\ = {2^2} - 2\left( {m - 3} \right) + {\left( {m - 3} \right)^2}\\ = 4 - 2m + 6 + {m^2} - 6m + 9\\ = {m^2} - 8m + 19\\ = {m^2} - 8m + 16 + 3\end{array}\)
\( = {\left( {m - 4} \right)^2} + 3 \ge 3\) với mọi \(m\).
Dấu “=” xảy ra là giá trị nhỏ nhất của biểu thức. Suy ra giá trị nhỏ nhất của P bằng 3 khi \(m - 4 = 0\) hay \(m = 4\).
Vậy \(m = 4\) thì P đạt giá trị nhỏ nhất.
Đề thi giữa kì 2 Toán 9 - Đề số 4: Tổng quan và Hướng dẫn
Kỳ thi giữa học kỳ 2 Toán 9 đóng vai trò quan trọng trong việc đánh giá năng lực học tập của học sinh sau một nửa năm học. Việc làm quen với các dạng đề thi và luyện tập thường xuyên là chìa khóa để đạt kết quả tốt. Bài viết này sẽ cung cấp thông tin chi tiết về Đề thi giữa kì 2 Toán 9 - Đề số 4 do tusach.vn biên soạn, cùng với những hướng dẫn hữu ích để các em có thể tự tin hơn khi bước vào phòng thi.
Cấu trúc đề thi giữa kì 2 Toán 9 - Đề số 4
Đề thi giữa kì 2 Toán 9 - Đề số 4 của tusach.vn được xây dựng theo cấu trúc phổ biến của các trường THCS, bao gồm các phần sau:
- Phần trắc nghiệm: (5-7 câu) Kiểm tra kiến thức cơ bản và khả năng vận dụng nhanh các công thức, định lý.
- Phần tự luận: (3-5 câu) Đòi hỏi học sinh phải trình bày chi tiết các bước giải, áp dụng kiến thức đã học để giải quyết các bài toán phức tạp hơn. Các dạng bài thường gặp bao gồm:
- Giải phương trình, hệ phương trình.
- Giải bài toán về hàm số bậc nhất.
- Giải bài toán về hình học (tam giác, tứ giác, đường tròn).
- Ứng dụng các định lý về tam giác đồng dạng.
Nội dung chi tiết đề thi và đáp án
Để giúp các em hiểu rõ hơn về đề thi, chúng ta sẽ đi vào phân tích chi tiết từng câu hỏi và đáp án của Đề thi giữa kì 2 Toán 9 - Đề số 4:
| Câu hỏi | Đáp án | Giải thích |
|---|---|---|
| Câu 1: (Trắc nghiệm) | A | Áp dụng định lý Pitago để tính độ dài cạnh huyền. |
| Câu 2: (Tự luận) | x = 2 | Giải phương trình bậc nhất một ẩn. |
| ... | ... | ... |
(Lưu ý: Bảng trên chỉ mang tính chất minh họa. Đáp án và giải thích chi tiết sẽ được cung cấp đầy đủ trong file đề thi tải về.)
Lợi ích khi luyện tập với Đề thi giữa kì 2 Toán 9 - Đề số 4
- Nắm vững kiến thức: Đề thi bao phủ đầy đủ các kiến thức trọng tâm của chương trình học kỳ 2.
- Rèn luyện kỹ năng: Giúp các em rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
- Làm quen với cấu trúc đề thi: Giúp các em làm quen với cấu trúc đề thi và phân bổ thời gian hợp lý trong quá trình làm bài.
- Đánh giá năng lực: Giúp các em tự đánh giá năng lực của mình và xác định những kiến thức còn yếu để tập trung ôn tập.
Lời khuyên khi làm bài thi giữa kì 2 Toán 9
- Đọc kỹ đề bài trước khi bắt đầu giải.
- Phân bổ thời gian hợp lý cho từng câu hỏi.
- Trình bày bài giải rõ ràng, mạch lạc.
- Kiểm tra lại bài làm trước khi nộp.
- Giữ bình tĩnh và tự tin trong quá trình làm bài.
Tải Đề thi giữa kì 2 Toán 9 - Đề số 4 ngay hôm nay!
Đừng bỏ lỡ cơ hội luyện tập với Đề thi giữa kì 2 Toán 9 - Đề số 4 của tusach.vn. Hãy tải ngay để chuẩn bị tốt nhất cho kỳ thi sắp tới!
Chúc các em học sinh đạt kết quả cao!