Đề thi học kì 1 Toán 9 - Đề số 4
Tổng quan nội dung
Đề thi học kì 1 Toán 9 - Đề số 4: Chuẩn bị tốt nhất cho kỳ thi
Đề thi học kì 1 Toán 9 - Đề số 4 là một trong những đề thi thử quan trọng giúp học sinh làm quen với cấu trúc đề thi chính thức và rèn luyện kỹ năng giải toán. Tại tusach.vn, chúng tôi cung cấp đề thi này kèm theo đáp án chi tiết, giúp học sinh tự đánh giá năng lực và cải thiện điểm số.
Đề thi này bao gồm các dạng bài tập thường gặp trong đề thi học kì, tập trung vào các chủ đề như đại số, hình học và giải toán thực tế. Hãy cùng tusach.vn chinh phục kỳ thi sắp tới!
Đề bài
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{4x - y = 2}\\{x + 3y = 7}\end{array}} \right.\) . Cặp số nào dưới đây là nghiệm của hệ phương trình đã cho?
- A.
\(\left( {2;2} \right)\).
- B.
\(\left( { - 1; - 2} \right)\).
- C.
\(\left( {1;2} \right)\).
- D.
\(\left( {2; - 2} \right)\).
Điều kiện xác định của phương trình \(\frac{{x + 2}}{{x - 4}} + 1 = \frac{1}{{x + 3}}\)
- A.
\(x \ne 4\) và \(x \ne 3\).
- B.
\(x \ne - 4\) và \(x \ne 3\).
- C.
\(x \ne 4\) và \(x \ne - 3\).
- D.
\(x \ne - 4\) và \(x \ne - 3\).
Số 3 là nghiệm của bất phương trình nào sau đây?
- A.
\(5x - 10 \le 0\).
- B.
\(2x + 1 > 0\).
- C.
\( - 5x + 7 \ge 0\).
- D.
\(2x - 5 < 0\).
Số nào sau đây có căn bậc hai số học bằng 4?
- A.
2.
- B.
4.
- C.
-2.
- D.
16.
Căn thức \(\sqrt {4 - 2x} \) xác định khi
- A.
\(x \ge 2\).
- B.
\(x \le 2\).
- C.
\(x \ge - 2\).
- D.
\(x \le - 2\).
Sau khi rút gọn biểu thức \(\frac{2}{{2 - \sqrt 3 }} + \frac{2}{{2 + \sqrt 3 }}\) ta được phân số tối giản \(\frac{a}{b}\), giá trị \(a + b\) là
- A.
10.
- B.
9.
- C.
8.
- D.
7.
Giá trị của biểu thức \(A = \sqrt {25} .\sqrt 9 - \sqrt[3]{{ - 27}}\) là
- A.
12.
- B.
15.
- C.
18.
- D.
21.
Tam giác ABC vuông tại A có AC = 6cm; BC = 12cm. Số đo góc ACB bằng
- A.
\(30^\circ \).
- B.
\(45^\circ \).
- C.
\(60^\circ \).
- D.
\(90^\circ \).
Dây lớn nhất của đường tròn \(\left( {O;3cm} \right)\) có độ dài bằng
- A.
8cm.
- B.
6cm.
- C.
4cm.
- D.
3cm.
Cho hình vẽ. Chọn khẳng định đúng.
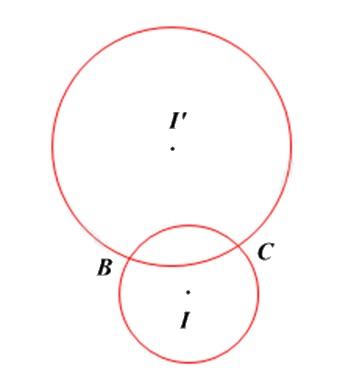
- A.
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) tiếp xúc trong.
- B.
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) tiếp xúc ngoài.
- C.
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) cắt nhau.
- D.
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) không giao nhau.
Tỉ số giữa độ dài cung \(n^\circ \) và độ dài đường tròn (cùng bán kính) bằng
- A.
\(\frac{n}{{360}}\).
- B.
\(\frac{n}{{180}}\).
- C.
\(\frac{n}{{120}}\).
- D.
\(\frac{n}{{90}}\).
Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Khi đó
- A.
AC là tiếp tuyến của đường tròn (B; 3).
- B.
AC là tiếp tuyến của đường tròn (C; 4).
- C.
BC là tiếp tuyến của đường tròn (A; 3).
- D.
AB là tiếp tuyến của đường tròn (C; 3).
Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{x - 2\sqrt x }}{{x - 4}}\) và \(Q = \frac{{\sqrt x {\rm{\;}} + 2}}{{\sqrt x {\rm{\;}} - 2}}{\mkern 1mu} {\mkern 1mu} \left( {x \ge 0;x \ne 4} \right)\)
a) Rút gọn P.
b) Tính giá trị của P khi \(x = 16\).
c) Biết \(M = P:Q\). Tìm giá trị của x để \({M^2} < \frac{1}{4}\).
Bác An chia số tiền \(630\) triệu đồng của mình cho hai khoản đầu tư. Sau một năm lợi nhuận thu về là \(157\) triệu đồng. Lợi nhuận của khoản đầu tư thứ nhất là \(10\% \), lợi nhuận của khoản đầu tư thứ hai là \(30\% \). Tính số tiền bác An đầu tư cho mỗi khoản?
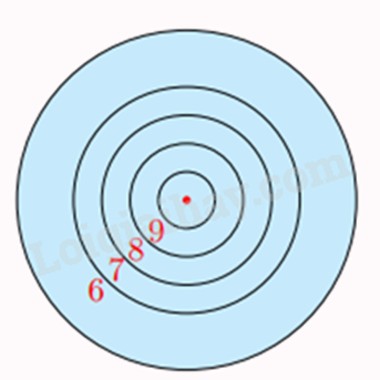
Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính \(5{\rm{cm}}\), \({\rm{10cm}}\), \(15{\rm{cm}}\), \(20{\rm{cm}}\) và \(30{\rm{cm}}\). Giả thiết rằng người chơi ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 9 (hình vành khuyên nằm giữa đường tròn thứ nhất và thứ hai). Biết rằng xác suất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
Cho đường tròn \((O)\), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn \((O')\) có đường kính CB.
a) Kẻ dây DE của đường tròn \((O)\) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
b) Gọi K là giao điểm của DB và đường tròn \((O')\). Chứng minh rằng ba điểm E, C, K thẳng hàng;
c) Chứng minh HK là tiếp tuyến của đường tròn \((O')\).
Vinasat-1 là vệ tinh viễn thông địa tĩnh đầu tiên của Việt Nam được phóng vào vũ trụ lúc 22 giờ 17 phút ngày 18 tháng 4 năm 2008 (giờ UTC). Dự án vệ tinh Vinasat-1 đã khởi động từ năm 1998 với tổng mức đầu tư là khoảng hơn 300 triệu USD. Việt Nam đã tiến hành đàm phán với 27 quốc gia và vùng lãnh thổ để có được vị trí 132 độ Đông trên quỹ đạo địa tĩnh.
Hãy tìm khoảng cách từ vệ tinh Vinasat-1 đến mặt đất. Biết rằng khi vệ tinh phát tín hiệu vô tuyến đến một điểm xa nhất trên mặt đất thì từ lúc phát tín hiệu đến mặt đất cho đến lúc vệ tinh thu lại được tín hiệu phản hồi mất khoảng thời gian là 0,28s. Trái đất được xem như một hình cầu có bán kính khoảng 6400km (ghi kết quả gần đúng chính xác đến hàng đơn vị), giả sử vận tốc sóng vô tuyến là \({3.10^8}\)m/s.

Lời giải và đáp án
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{4x - y = 2}\\{x + 3y = 7}\end{array}} \right.\) . Cặp số nào dưới đây là nghiệm của hệ phương trình đã cho?
- A.
\(\left( {2;2} \right)\).
- B.
\(\left( { - 1; - 2} \right)\).
- C.
\(\left( {1;2} \right)\).
- D.
\(\left( {2; - 2} \right)\).
Đáp án : C
Giải hệ phương trình hoặc sử dụng máy tính cầm tay để tính nghiệm của hệ phương trình.
Sử dụng máy tính cầm tay, ta tính được nghiệm của hệ phương trình là \(\left( {1;2} \right)\).
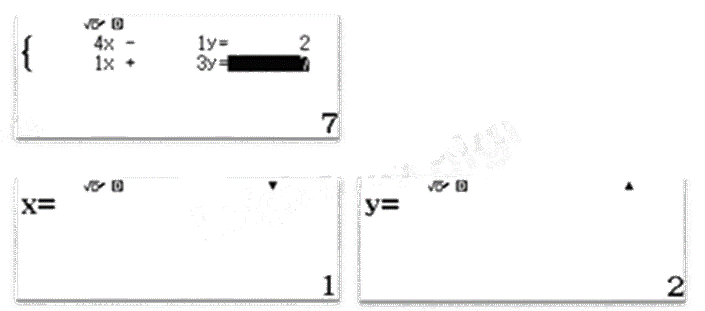
Đáp án C
Điều kiện xác định của phương trình \(\frac{{x + 2}}{{x - 4}} + 1 = \frac{1}{{x + 3}}\)
- A.
\(x \ne 4\) và \(x \ne 3\).
- B.
\(x \ne - 4\) và \(x \ne 3\).
- C.
\(x \ne 4\) và \(x \ne - 3\).
- D.
\(x \ne - 4\) và \(x \ne - 3\).
Đáp án : C
Điều kiện xác định của phương trình chứa ẩn ở mẫu là mẫu thức khác 0.
Điều kiện xác định của phương trình \(\frac{{x + 2}}{{x - 4}} + 1 = \frac{1}{{x + 3}}\) là \(x - 4 \ne 0\) và \(x + 3 \ne 0\).
Suy ra \(x \ne 4\) và \(x \ne - 3\).
Đáp án C
Số 3 là nghiệm của bất phương trình nào sau đây?
- A.
\(5x - 10 \le 0\).
- B.
\(2x + 1 > 0\).
- C.
\( - 5x + 7 \ge 0\).
- D.
\(2x - 5 < 0\).
Đáp án : B
Thay \(x = 3\) vào các bất đẳng thức để xác định.
Với \(x = 3\) thì \(5.3 - 10 = 15 > 0\) nên \(x = 3\) không phải nghiệm của \(5x - 10 \le 0\).
Với \(x = 3\) thì \(2.3 + 1 = 7 > 0\) nên \(x = 3\) là nghiệm của \(2x + 1 > 0\).
Với \(x = 3\) thì \( - 5.3 + 7 = - 8 < 0\) nên \(x = 3\) không phải nghiệm của \( - 5x + 7 \ge 0\).
Với \(x = 3\) thì \(2.3 - 5 = 1 > 0\) nên \(x = 3\) không phải nghiệm của \(2x - 5 < 0\).
Đáp án B
Số nào sau đây có căn bậc hai số học bằng 4?
- A.
2.
- B.
4.
- C.
-2.
- D.
16.
Đáp án : D
Số \(x\) có căn bậc hai số học bằng a thì \(x = {a^2}\).
Số có căn bậc hai số học bằng 4 là \({4^2} = 16\).
Đáp án D
Căn thức \(\sqrt {4 - 2x} \) xác định khi
- A.
\(x \ge 2\).
- B.
\(x \le 2\).
- C.
\(x \ge - 2\).
- D.
\(x \le - 2\).
Đáp án : B
Căn thức \(\sqrt A \) xác định khi \(A \ge 0\).
Căn thức \(\sqrt {4 - 2x} \) xác định khi \(4 - 2x \ge 0\) suy ra \(x \le 2\).
Đáp án B
Sau khi rút gọn biểu thức \(\frac{2}{{2 - \sqrt 3 }} + \frac{2}{{2 + \sqrt 3 }}\) ta được phân số tối giản \(\frac{a}{b}\), giá trị \(a + b\) là
- A.
10.
- B.
9.
- C.
8.
- D.
7.
Đáp án : B
Rút gọn biểu thức bằng cách trục căn thức, sau đó tính tổng a + b.
\(\frac{2}{{2 - \sqrt 3 }} + \frac{2}{{2 + \sqrt 3 }} = \frac{{2\left( {2 + \sqrt 3 } \right) + 2\left( {2 - \sqrt 3 } \right)}}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}} = \frac{{4 + 2\sqrt 3 + 4 - 2\sqrt 3 }}{{4 - 3}} = \frac{8}{1}\).
Suy ra \(a + b = 8 + 1 = 9\).
Đáp án B
Giá trị của biểu thức \(A = \sqrt {25} .\sqrt 9 - \sqrt[3]{{ - 27}}\) là
- A.
12.
- B.
15.
- C.
18.
- D.
21.
Đáp án : C
Sử dụng tính chất của căn bậc hai, căn bậc ba để tính.
\(A = \sqrt {25} .\sqrt 9 - \sqrt[3]{{ - 27}} = 5.3 - \left( { - 3} \right) = 15 + 3 = 18\)
Đáp án C
Tam giác ABC vuông tại A có AC = 6cm; BC = 12cm. Số đo góc ACB bằng
- A.
\(30^\circ \).
- B.
\(45^\circ \).
- C.
\(60^\circ \).
- D.
\(90^\circ \).
Đáp án : C
Sử dụng kiến thức về tỉ số lượng giác và tìm số đo góc khi biết tỉ số lượng giác.
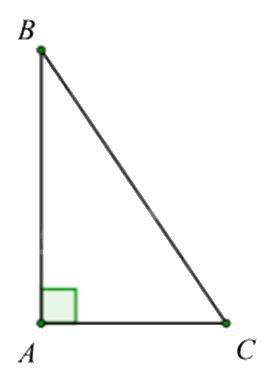
Áp dụng hệ thức lượng trong tam giác vuông vào tam giác ABC, ta có:
\(\cos ACB = \frac{{AC}}{{BC}} = \frac{6}{{12}} = \frac{1}{2}\) suy ra \(\widehat {ACB} = 60^\circ \).
Đáp án C
Dây lớn nhất của đường tròn \(\left( {O;3cm} \right)\) có độ dài bằng
- A.
8cm.
- B.
6cm.
- C.
4cm.
- D.
3cm.
Đáp án : B
Trong một đường tròn, đường kính là dây cung lớn nhất.
Dây lớn nhất của đường tròn là đường kính, do đó độ dài là 3.2 = 6cm.
Đáp án B
Cho hình vẽ. Chọn khẳng định đúng.
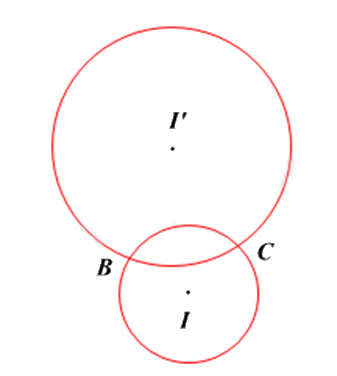
- A.
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) tiếp xúc trong.
- B.
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) tiếp xúc ngoài.
- C.
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) cắt nhau.
- D.
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) không giao nhau.
Đáp án : C
Quan sát hình vẽ để xác định.
Hai đường tròn \(\left( I \right)\) và \(\left( {I{}'} \right)\) có hai điểm chung nên chúng cắt nhau.
Đáp án C
Tỉ số giữa độ dài cung \(n^\circ \) và độ dài đường tròn (cùng bán kính) bằng
- A.
\(\frac{n}{{360}}\).
- B.
\(\frac{n}{{180}}\).
- C.
\(\frac{n}{{120}}\).
- D.
\(\frac{n}{{90}}\).
Đáp án : A
Sử dụng công thức tính độ dài cung tròn và độ dài đường tròn.
Độ dài cung tròn \(n^\circ \): \(l = \frac{{n\pi R}}{{180}}\)
Độ dài đường tròn: \(C = 2\pi R\)
Tỉ số giữa độ dài cung \(n^\circ \) và độ dài đường tròn (cùng bán kính) bằng:
\(\frac{l}{C} = \frac{{n\pi R}}{{180}}:2\pi R = \frac{{n\pi R}}{{360\pi R}} = \frac{n}{{360}}\).
Đáp án A
Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Khi đó
- A.
AC là tiếp tuyến của đường tròn (B; 3).
- B.
AC là tiếp tuyến của đường tròn (C; 4).
- C.
BC là tiếp tuyến của đường tròn (A; 3).
- D.
AB là tiếp tuyến của đường tròn (C; 3).
Đáp án : A
Sử dụng định lí Pythagore đảo và tính chất tiếp tuyến để kiểm tra.
Tam giác ABC có: \(A{B^2} + A{C^2} = {3^2} + {4^2} = {5^2} = B{C^2}\) nên tam giác ABC vuông tại A (theo định lí Pythagore đảo).
Suy ra AB vuông góc với AC tại A. Mà A thuộc đường tròn (B; AB) hay (B; 3).
Do đó AC là tiếp tuyến của đường tròn (B; 3).
Đáp án A
Cho biểu thức \(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{x - 2\sqrt x }}{{x - 4}}\) và \(Q = \frac{{\sqrt x {\rm{\;}} + 2}}{{\sqrt x {\rm{\;}} - 2}}{\mkern 1mu} {\mkern 1mu} \left( {x \ge 0;x \ne 4} \right)\)
a) Rút gọn P.
b) Tính giá trị của P khi \(x = 16\).
c) Biết \(M = P:Q\). Tìm giá trị của x để \({M^2} < \frac{1}{4}\).
a) Rút gọn phân thức trước rồi rút gọn biểu thức.
b) Thay \(x = 16\) vào P để tính giá trị.
c) Tìm M thay vào \({M^2} < \frac{1}{4}\) để tìm x, lưu ý điều kiện đầu bài.
a) Ta có:
\(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{x - 2\sqrt x }}{{x - 4}}\)
\(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{\sqrt x \left( {\sqrt x {\rm{\;}} - 2} \right)}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} + 2} \right)}}\)
\(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} - \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}\)
\(P = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}}\).
b) Thay \(x = 16\) vào P, ta được:
\(P = \frac{{\sqrt {16} }}{{\sqrt {16} - 2}} = \frac{4}{{4 - 2}} = \frac{4}{2} = 2\).
Vậy với \(x = 16\) thì \(P = 2\).
c) Ta có:
\(M = P:Q = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}}:\frac{{\sqrt x {\rm{\;}} + 2}}{{\sqrt x {\rm{\;}} - 2}}{\mkern 1mu} \)
\( = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} - 2}}.\frac{{\sqrt x {\rm{\;}} - 2}}{{\sqrt x {\rm{\;}} + 2}} = \frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}\)
Vì \({M^2} < \frac{1}{4}\) nên \({\left( {\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}} \right)^2} < \frac{1}{4}\). Suy ra \(\left| {\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}}} \right| < \frac{1}{2}\)
Vì \(\sqrt x > 0\) nên \(\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} > 0\)
Do đó \(\frac{{\sqrt x }}{{\sqrt x {\rm{\;}} + 2}} < \frac{1}{2}\)
\(2\sqrt x {\rm{\;}} < \sqrt x {\rm{\;}} + 2\)
\(\sqrt x {\rm{\;}} < 2\)
\(x < 4\)
Kết hợp điều kiện \(x \ge 0;x \ne 4\) ta được \(0 \le x < 4\).
Vậy để \({M^2} < \frac{1}{4}\) thì \(0 \le x < 4\).
Bác An chia số tiền \(630\) triệu đồng của mình cho hai khoản đầu tư. Sau một năm lợi nhuận thu về là \(157\) triệu đồng. Lợi nhuận của khoản đầu tư thứ nhất là \(10\% \), lợi nhuận của khoản đầu tư thứ hai là \(30\% \). Tính số tiền bác An đầu tư cho mỗi khoản?
Gọi số tiền đầu tư cho mỗi khoản lần lượt là \(x,y\) (\(x,y \in {\mathbb{N}^*};x,y \le 630\) )
Lập hệ phương trình với x và y.
Từ đó giải hệ phương trình.
Gọi số tiền đầu tư cho mỗi khoản lần lượt là \(x,y\) (\(x,y \in {\mathbb{N}^*};x,y \le 630\) )
Vì bác An chia số tiền \(630\) triệu đồng của mình cho hai khoản đầu tư nên \(x + y = 630\) (triệu đồng)
Vì lợi nhuận của khoản đầu tư thứ nhất là \(10\% \), lợi nhuận của khoản đầu tư thứ hai là \(30\% \) và sau một năm lợi nhuận thu về là \(157\) triệu đồng nên \(10\% x + 30\% y = 157\) hay \(0,1x + 0,3y = 157\)
Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{0,1x + 0,3y = 157}\end{array}} \right.\)
Giải hệ phương trình:
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{0,1x + 0,3y = 157}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{x + 3y = 1570}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{2y = 940}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x + y = 630}\\{y = 470}\end{array}} \right.\\\left\{ {\begin{array}{*{20}{l}}{x = 160(TM)}\\{y = 470(TM)}\end{array}} \right.\end{array}\)
Vậy khoản đầu tư thứ nhất là \(160\) triệu đồng, khoản đầu tư thứ hai là \(470\) triệu đồng.
Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính \(5{\rm{cm}}\), \({\rm{10cm}}\), \(15{\rm{cm}}\), \(20{\rm{cm}}\) và \(30{\rm{cm}}\). Giả thiết rằng người chơi ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 9 (hình vành khuyên nằm giữa đường tròn thứ nhất và thứ hai). Biết rằng xác suất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
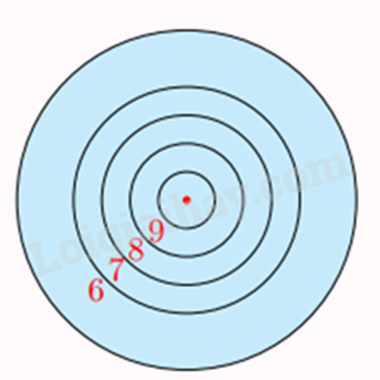
Sử dụng công thức tính diện tích hình vành khuyên để tính diện tích hình vành khuyên nằm giữa đường tròn thứ nhất và thứ hai: \({S_{vk}} = \pi \left( {{R^2} - {r^2}} \right)\) với \(R > r\).
Sử dụng công thức tính diện tích hình tròn để tính diện tích hình tròn lớn nhất: \(S = \pi {r^2}\)
Tính tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất
Vì bán kính của đường tròn thứ nhất và thứ hai lần lượt là 5cm và 10cm nên diện tích hình vành khuyên nằm giữa đường tròn thứ nhất và thứ hai là:
\({S_{vk}} = \pi \left( {{{10}^2} - {5^2}} \right) = 75\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Vì hình tròn lớn nhất có bán kính là 30cm nên diện tích hình tròn lớn nhất:
\(S = {30^2} \cdot \pi = 900\pi \left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Xác suất ném trúng vòng 9 là: \(\frac{{{S_{vk}}}}{S} = \frac{{75\pi }}{{900\pi }} = \frac{1}{{12}}\)
Vậy xác suất ném trúng vòng 9 là \(\frac{1}{{12}}\).
Cho đường tròn \((O)\), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn \((O')\) có đường kính CB.
a) Kẻ dây DE của đường tròn \((O)\) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
b) Gọi K là giao điểm của DB và đường tròn \((O')\). Chứng minh rằng ba điểm E, C, K thẳng hàng;
c) Chứng minh HK là tiếp tuyến của đường tròn \((O')\).
a) Chứng minh \(\Delta ODH = \Delta OEH\left( {ch - cgv} \right)\) suy ra DH = HE
Tứ giác có hai đường chéo vuông góc tại trung điểm của mỗi đường là hình thoi.
b) Chứng minh \(EC \bot DB\) và \(CK \bot DB\) nên E, C, K thẳng hàng (tiên đề Euclid).
c) Chứng minh \(\widehat {HKE} = \widehat {HEK}\) và \(\widehat {O'KC} = \widehat {HCE}\), suy ra \(\widehat {HKE} + \widehat {O'KC} = 90^\circ \) nên \(\widehat {HKO'} = 90^\circ \).
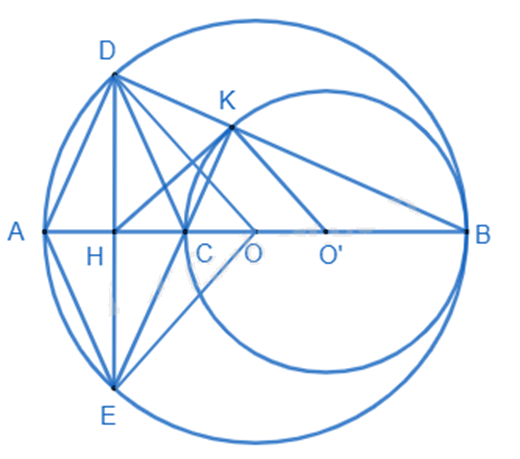
a) Xét \(\Delta ODH\) và \(\Delta OEH\) có:
\(\begin{array}{l}\widehat {OHD} = \widehat {OHE} = 90^\circ \\OD = OE = R\\OH\,{\rm{chung}}\end{array}\)
Suy ra \(\Delta ODH = \Delta OEH\left( {ch - cgv} \right)\)
Do đó DH = HE (hai cạnh tương ứng).
Mà \(H \in DE\) suy ra H là trung điểm của BE.
Tứ giác ADCE có H là trung điểm của hai đường chéo DE, AC và \(AC \bot DE\) tại H nên tứ giác ADCE là hình thoi.
b) Ta có \(AD \bot DB\) (Vì AB là đường kính của \((O)\) và \(D \in (O)\)) nên suy ra \(EC \bot DB\) (1) (Vì tứ giác ADCE là hình thoi).
Lại có \(CK \bot KB\) (Vì CB là đường kính của \((O')\) và \(K \in (O')\)) hay \(CK \bot DB\) (2).
Từ (1) và (2) suy ra E, C, K thẳng hàng (tiên đề Euclid).
c) Xét \(\Delta DKE\) vuông tại K có KH là đường trung tuyến ứng với cạnh huyền nên \(HK = HE = \frac{1}{2}DE\).
Suy ra \(\Delta HKE\) cân tại H, do đó \(\widehat {HKE} = \widehat {HEK}\).
Lại có \(\widehat {O'KC} = \widehat {O'CK}\) (tam giác O’CK cân tại O’) và \(\widehat {O'CK} = \widehat {HCE}\) (2 góc đối đỉnh) do đó \(\widehat {O'KC} = \widehat {HCE}\).
Mà \(\widehat {HEK} + \widehat {HCE} = 90^\circ \) (hai góc phụ nhau) nên \(\widehat {HKE} + \widehat {O'KC} = 90^\circ \), suy ra \(\widehat {HKO'} = 90^\circ \)
Do đó \(HK \bot KO'\).
Vậy HK là tiếp tuyến của \((O')\) tại K .
Vinasat-1 là vệ tinh viễn thông địa tĩnh đầu tiên của Việt Nam được phóng vào vũ trụ lúc 22 giờ 17 phút ngày 18 tháng 4 năm 2008 (giờ UTC). Dự án vệ tinh Vinasat-1 đã khởi động từ năm 1998 với tổng mức đầu tư là khoảng hơn 300 triệu USD. Việt Nam đã tiến hành đàm phán với 27 quốc gia và vùng lãnh thổ để có được vị trí 132 độ Đông trên quỹ đạo địa tĩnh.
Hãy tìm khoảng cách từ vệ tinh Vinasat-1 đến mặt đất. Biết rằng khi vệ tinh phát tín hiệu vô tuyến đến một điểm xa nhất trên mặt đất thì từ lúc phát tín hiệu đến mặt đất cho đến lúc vệ tinh thu lại được tín hiệu phản hồi mất khoảng thời gian là 0,28s. Trái đất được xem như một hình cầu có bán kính khoảng 6400km (ghi kết quả gần đúng chính xác đến hàng đơn vị), giả sử vận tốc sóng vô tuyến là \({3.10^8}\)m/s.
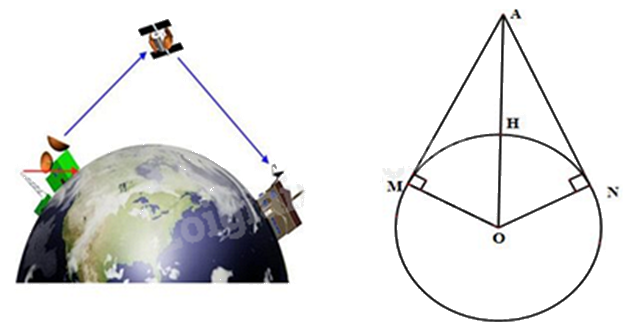
Khoảng cách từ vệ tính đến mặt đất chính là độ dài của đoạn AM hoặc AN.
Ta cần sử dụng công thức \(S = vt\), trong đó S là quãng đường truyền tín hiệu đi được trong khoảng thời gian t.
Xác định thời gian tín hiệu truyền từ A đến M.

Do thời gian từ lúc truyền tín hiệu đến lúc nhận lại tín hiệu là 0,28s, nên thời gian tín hiệu truyền từ A đến M là:
\(0,28:2 = 0,14\left( s \right)\)
Độ dài đoạn AM cũng là quãng đường tín hiệu truyền đi được trong 0,14s là:
\(S = AM = vt = {3.10^8}.0,14 = 42\,000\,000\left( m \right) = 42\,000\left( {km} \right)\)
Vị trí xa nhất trên trái đất có thể nhận tín hiệu từ vệ tinh là vô số điểm M (với AM là tiếp tuyến kẻ từ A đến đường tròn tâm O).
Vì AM là tiếp tuyến (O) nên \(OM \bot AM\) tại M.
Áp dụng định lý Pythagore vào tam giác vuông AMO ta có:
\(O{A^2} = O{M^2} + M{A^2} = 6\,{400^2} + 42\,{000^2} = 1\,804\,960\,000\)
Suy ra \(OA = \sqrt {1\,804\,960\,000} = 42\,485\left( {km} \right)\).
Khoảng cách từ vệ tinh Vinasat-1 đến mặt đất là độ dài đoạn AH:
\(AH = AO - OH = 42\,485 - 6\,400 = 36\,085\left( {km} \right)\).
Đề thi học kì 1 Toán 9 - Đề số 4: Tổng quan và Hướng dẫn Ôn tập
Kỳ thi học kì 1 Toán 9 là một bước quan trọng trong quá trình học tập của các em học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Đề thi học kì 1 Toán 9 - Đề số 4 tại tusach.vn được thiết kế để giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự đánh giá năng lực của bản thân.
Nội dung Đề thi học kì 1 Toán 9 - Đề số 4
Đề thi này bao gồm các dạng bài tập thường gặp trong đề thi học kì 1 Toán 9, được phân chia theo các chủ đề chính:
- Đại số: Các bài toán về biểu thức đại số, phương trình bậc nhất một ẩn, hệ phương trình bậc nhất hai ẩn, bất phương trình.
- Hình học: Các bài toán về tam giác, tứ giác, đường tròn, hệ thức lượng trong tam giác vuông.
- Giải toán thực tế: Các bài toán ứng dụng kiến thức toán học vào giải quyết các vấn đề thực tế.
Tại sao nên luyện tập với Đề thi học kì 1 Toán 9 - Đề số 4 của tusach.vn?
- Bám sát cấu trúc đề thi chính thức: Đề thi được xây dựng dựa trên cấu trúc đề thi học kì 1 Toán 9 của Bộ Giáo dục và Đào tạo.
- Đáp án chi tiết: Kèm theo đề thi là đáp án chi tiết, giúp học sinh hiểu rõ cách giải và tự đánh giá năng lực của bản thân.
- Giao diện thân thiện: Website tusach.vn có giao diện thân thiện, dễ sử dụng, giúp học sinh dễ dàng tìm kiếm và tải đề thi.
- Miễn phí: Đề thi và đáp án được cung cấp hoàn toàn miễn phí.
Hướng dẫn ôn tập hiệu quả cho kỳ thi học kì 1 Toán 9
Để ôn tập hiệu quả cho kỳ thi học kì 1 Toán 9, các em học sinh nên:
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các công thức, định lý và tính chất quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập thường gặp.
- Sử dụng các tài liệu ôn tập: Tham khảo các đề thi thử, bài tập trắc nghiệm và các tài liệu ôn tập khác để bổ sung kiến thức và kỹ năng.
- Hỏi thầy cô giáo: Nếu gặp khó khăn trong quá trình học tập, hãy hỏi thầy cô giáo để được giải đáp và hướng dẫn.
Ví dụ một số dạng bài tập trong Đề thi học kì 1 Toán 9 - Đề số 4
| Dạng bài tập | Ví dụ |
|---|---|
| Giải phương trình | Giải phương trình: 2x + 3 = 7 |
| Tính góc trong tam giác | Cho tam giác ABC vuông tại A, biết góc B = 60 độ. Tính góc C. |
| Ứng dụng hệ thức lượng | Cho tam giác ABC vuông tại A, đường cao AH. Tính độ dài AH biết AB = 6cm, AC = 8cm. |
Lời khuyên cuối cùng
Hãy sử dụng Đề thi học kì 1 Toán 9 - Đề số 4 của tusach.vn như một công cụ hỗ trợ đắc lực trong quá trình ôn tập của bạn. Chúc các em học sinh đạt kết quả tốt nhất trong kỳ thi sắp tới!