Đề thi học kì 2 Toán 11 - Đề số 4
Tổng quan nội dung
Đề thi học kì 2 Toán 11 - Đề số 4
Chào mừng bạn đến với Đề thi học kì 2 Toán 11 - Đề số 4 tại tusach.vn. Đề thi này được biên soạn theo chuẩn chương trình học kì 2 môn Toán lớp 11, giúp các em học sinh ôn tập và đánh giá kiến thức đã học.
Đề thi bao gồm các dạng bài tập khác nhau, từ trắc nghiệm đến tự luận, bao phủ đầy đủ các chủ đề quan trọng trong chương trình học.
Đề bài
Tính giá trị của biểu thức \(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}}\):
- A.\(288\)
- B.\(\frac{{32}}{9}\)
- C.\(\frac{2}{9}\)
- D.\(18\)
Trong các hình sau, hình nào là dạng đồ thị của hàm số\(y = {\log _a}x,0 < a < 1\)
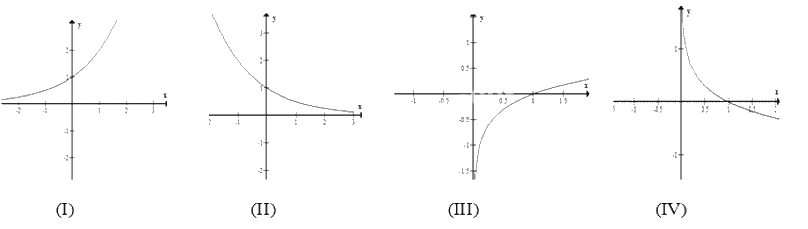
- A.(I).
- B.
(II).
- C.(IV).
- D.(III).
Cho hình chóp \(SABC\) có \(SA \bot \left( {ABC} \right).\) Gọi \(H,{\rm{ }}K\) lần lượt là trực tâm các tam giác \(SBC\) và\(ABC\). Mệnh đề nào sai trong các mệnh đề sau?
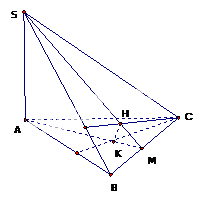
- A.\(BC \bot \left( {SAH} \right).\)
- B.\(HK \bot \left( {SBC} \right).\)
- C.\(BC \bot \left( {SAB} \right).\)
- D.
\(SH,{\rm{ }}AK{\rm{ }} , {\rm{ }}BC\) đồng quy tại một điểm
Cho tứ diện \(\frac{a}{3}\) trong đó\(\left( {ACB'} \right)//(DA'C')\), \(d\left( {\left( {ACB'} \right),\left( {DA'C'} \right)} \right) = d\left( {D;\left( {ACB'} \right)} \right) = d\left( {B;\left( {ACB'} \right)} \right)\), \(BA = BB' = BC = a\) vuông góc với nhau từng đôi một và\(AB' = AC = CB' = a\sqrt 2 \), \(B.ACB'\),\(I\). Khoảng cách từ \(AC,\,\,G\) đến đường thẳng \(ACB'\) bằng
- A.\(d\left( {B;\left( {ACB'} \right)} \right) = BG\)
- B.\(ACB'\)
- C.\(B'I = a\sqrt 2 .\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{2}\)
- D.\(B'G = \frac{2}{3}B'I = \frac{{a\sqrt 6 }}{3}\)
Tại một cuộc hội thảo quốc tế có 50 nhà khoa học trong đó có 31 người thành thạo tiếng Anh, 21 người thành thạo tiếng Pháp và 5 người thành thạo cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một người dự hội thảo. Xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là:
- A.\(\frac{{47}}{{50}}\)
- B.\(\frac{{37}}{{50}}\)
- C.\(\frac{{39}}{{50}}\)
- D.\(\frac{{41}}{{50}}\)
Cho hàm số \(y = - {x^3} + 3x - 2\) có đồ thị \(\left( C \right).\)Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung là
- A.\(y = - 2x + 1\)
- B.\(y = 2x + 1\)
- C.\(y = 3x - 2\)
- D.\(y = - 3x - 2\)
Cho hàm số \(y = {\sin ^2}x\). Khi đó đạo hàm y’ là
- A.\(y' = {\cos ^2}x\)
- B.\(y' = \sin 2x\)
- C.\(y' = \frac{{ - 3}}{{{{\sin }^2}x}} + 1\)
- D.\(y' = \frac{3}{{{{\sin }^2}x}}\)
Hàm số \(y = \sqrt {2 + 2{x^2}} \)có đạo hàm \(y' = \frac{{a + bx}}{{\sqrt {2 + 2{x^2}} }}\). Khi đó \(S = a - 2b\) có kết quả bằng
- A.\(S = - 4\)
- B.\(S = 10\)
- C.\(S = - 6\)
- D.\(S = 8\)
Hàm số \(y = \frac{{{x^2} + x}}{{x - 1}}\)có đạo hàm \(y' = \frac{{a{x^2} + bx + c}}{{{{(x - 1)}^2}}}\). Khi đó \(S = a + b + c\) có kết quả là:
- A.1
- B.2
- C.5
- D.2
Một chất điểm chuyển động có phương trình \(s\left( t \right) = {t^2} + 1\) (\(t\) tính bằng giây, \(s\) tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng
- A.\(1m/s.\)
- B.\(6m/s.\)
- C.\(4m/s.\)
- D.\(0m/s.\)
Hai người cùng bắn vào 1 bia. Người thứ nhất có xác suất bắn trúng là 60%, xác suất bắn trúng của người thứ 2 là 70%. Xác suất để cả hai người cùng bắn trật bằng
- A.
0,42
- B.
0,21
- C.
0,12
- D.
0,48
Hàm số \(y = {x^5}\) có đạo hàm là:
- A.\(y' = 5{x^6}\)
- B.\(y' = 4{x^5}\)
- C.\(y' = 5x\)
- D.\(y' = 5{x^4}\)
Một chất điểm chuyển động có phương trình chuyển động là \(s = s(t) = - {t^3} + 9{t^2} + t + 10\) (t được tính bằng giây, s được tính bẳng mét)
a) Đạo hàm của hàm số \(s(t)\) tại thời điểm \({t_0}\) là: \({t_0} + 4\)
b) Tính vận tốc tức thời của chuyển động tại thời điểm \(t = 5\)là \(16(m/s)\)
c) Tính gia tốc tức thời của chuyển động tại thời điểm \(t = 5\) là \(12(m/{s^2})\)
d) Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là t = 2 (s)
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x + 1}}{{3x}}(C)\)
a) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Oy là: \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Ox là là\(y = - \frac{1}{3}x - \frac{1}{3}\)
c) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) tại giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là: \(y = - 3x + \frac{7}{3}\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = - \frac{1}{3}\) là \(y = - \frac{1}{3}x + 1\) và \(y = - \frac{1}{3}x - \frac{1}{3}\)
Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm của cạnh BC. AH, IJ là đường cao tam giác AID.
a) \(BC \bot (AID)\)
b) \(AH \bot (BCD)\)
c) IJ là đường vuông góc chung của AD và BC
d) H là trọng tâm tam giác BCD
Trong đợt kiểm tra cuối học kì II lớp 11 của các trường trung học phổ thông, thống kê cho thấy có 93% học sinh tỉnh X đạt yêu cầu; 87% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y. Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập
a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là\(0,7809\)
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là \(0,0091\)
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là \(0,1818\)
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là \(0,9909\)
Tính giới hạn: \(I = \mathop {lim}\limits_{x \to - 3} \frac{{{x^2} + 2x - 3}}{{{x^2} + 5x + 6}}\)
Cho hàm số : \(y = 5{x^4} - 3{x^3} + 6x - \sqrt 7 \). Tính \(f'\left( 0 \right)\).
Cho hình chóp tứ giác đều\(S.ABCD\)có tất cả các cạnh bằng \(a\). Tính khoảng cách từ đỉnh \(S\) đến mặt phẳng \((ABCD).\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\).Cạnh bên \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\sqrt 2 \).Góc giữa đường thẳng \(SC\)và mặt phẳng \(\left( {ABCD} \right)\)bằng
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) với \(a,b,c \in \mathbb{R}\). Biết rằng đồ thị hàm số đi qua hai điểm \(A\left( {1; - 3} \right)\) và \(B\left( {2;3} \right)\), đồng thời tiếp tuyến của đồ thị tại điểm có hoành độ bằng \( - 1\) có hệ số góc bằng 2. Tính tổng \(S = a + b + c\).
Cho hàm số \(y = \frac{{x - 2}}{{x + 3}}\) có đồ thị \(\left( C \right).\) Tìm điểm \(M\) trên đồ thị \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)tạo với hai trục tọa độ một tam giác có diện tích bằng \(\frac{{18}}{5}.\)
Lời giải và đáp án
Tính giá trị của biểu thức \(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}}\):
- A.\(288\)
- B.\(\frac{{32}}{9}\)
- C.\(\frac{2}{9}\)
- D.\(18\)
Đáp án : B
Sử dụng công thức lũy thừa
\(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}} = \frac{{{4^{5 + \sqrt 3 }}{{.3}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}} = \frac{{{2^{10 + 2\sqrt 3 }}{{.3}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}} = \frac{{{2^5}}}{{{3^2}}} = \frac{{32}}{9}\)
Đáp án B.
Trong các hình sau, hình nào là dạng đồ thị của hàm số\(y = {\log _a}x,0 < a < 1\)
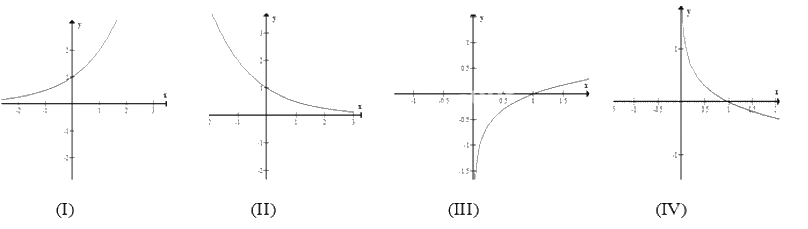
- A.(I).
- B.
(II).
- C.(IV).
- D.(III).
Đáp án : B
Hàm số \(y = {\log _a}x\) có đồ thị luôn đi qua điểm (1;0) và nghịch biến khi 0 <a<1
Do 0<a<1 nên đồ thị hàm số có chiều đi xuống từ trái qua phải
Đồ thị luôn đi qua điểm (1;0)
Đáp án B.
Cho hình chóp \(SABC\) có \(SA \bot \left( {ABC} \right).\) Gọi \(H,{\rm{ }}K\) lần lượt là trực tâm các tam giác \(SBC\) và\(ABC\). Mệnh đề nào sai trong các mệnh đề sau?
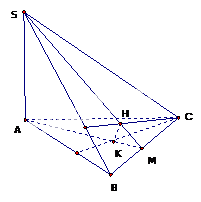
- A.\(BC \bot \left( {SAH} \right).\)
- B.\(HK \bot \left( {SBC} \right).\)
- C.\(BC \bot \left( {SAB} \right).\)
- D.
\(SH,{\rm{ }}AK{\rm{ }} , {\rm{ }}BC\) đồng quy tại một điểm
Đáp án : C
Sử dụng định lý đường thẳng vuông góc mặt phẳng
a)
\(\left\{ \begin{array}{l}BC \bot SA\,\,(Do\,\,SA \bot (ABC))\\BC \bot SH\\SA,SH \subset (SAH)\\SA \cap SH\end{array} \right. \Rightarrow BC \bot (SAH)\)
b)\(\left\{ \begin{array}{l}CK \bot SA\,\,\\CK \bot AB\\SA,AB \subset (SAB)\\SA \cap AB\end{array} \right. \Rightarrow CK \bot (SAB) \Rightarrow CK \bot SB\)
Lại có: \(\left\{ \begin{array}{l}SB \bot CK - cmt\,\,\\SB \bot CH\\CH,CK \subset (CKH)\\CH \cap CK\end{array} \right. \Rightarrow SB \bot (CKH) \Rightarrow SB \bot HK\)
Ta có: \(\left\{ \begin{array}{l}HK \bot SB - cmt\,\,\\HK \bot BC\,(Do\,BC \bot (SAB))\\SB,BC \subset (SBC)\\SB \cap BC\end{array} \right. \Rightarrow HK \bot (SBC)\)
c)Do \(CK \bot (SAB)\)nên BC không thể vuông góc với (SAB)
d) Gọi M là giao điểm của SH và BC. Do \(BC \bot (SAH)\) nên \(BC \bot AM\) hay đường thẳng AM trùng với đường thẳng AK. Hay SH, AK, BC đồng quy
Đáp án C.
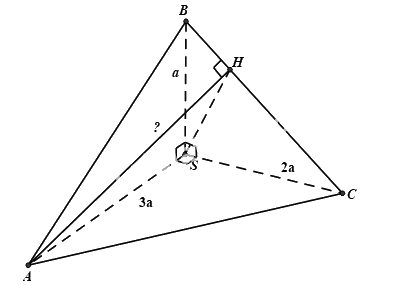
Cho tứ diện \(\frac{a}{3}\) trong đó\(\left( {ACB'} \right)//(DA'C')\), \(d\left( {\left( {ACB'} \right),\left( {DA'C'} \right)} \right) = d\left( {D;\left( {ACB'} \right)} \right) = d\left( {B;\left( {ACB'} \right)} \right)\), \(BA = BB' = BC = a\) vuông góc với nhau từng đôi một và\(AB' = AC = CB' = a\sqrt 2 \), \(B.ACB'\),\(I\). Khoảng cách từ \(AC,\,\,G\) đến đường thẳng \(ACB'\) bằng
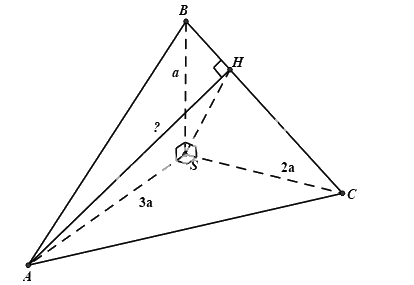
- A.\(d\left( {B;\left( {ACB'} \right)} \right) = BG\)
- B.\(ACB'\)
- C.\(B'I = a\sqrt 2 .\frac{{\sqrt 3 }}{2} = \frac{{a\sqrt 6 }}{2}\)
- D.\(B'G = \frac{2}{3}B'I = \frac{{a\sqrt 6 }}{3}\)
Đáp án : B
Sử dụng phương pháp tính khoảng cách từ đường thẳng tới mặt phẳng
Dựng \(AH \bot BC \Rightarrow d(A,BC) = AH\)
\(\begin{array}{l}\left\{ \begin{array}{l}SA \bot (SBC)\\AH \bot BC\end{array} \right. \Rightarrow SA \bot BC\\ \Rightarrow BC \bot (SAH) \Rightarrow BC \bot SH\end{array}\)
Xét tam giác SBC vuông tại S có SH là đường cao ta có:
\(\begin{array}{l}\frac{1}{{S{H^2}}} = \frac{1}{{S{B^2}}} + \frac{1}{{S{C^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{4{a^2}}} = \frac{5}{{4{a^2}}} \Rightarrow S{H^2} = \frac{{4{a^2}}}{5}\\ \Rightarrow SH = \frac{{2a\sqrt 5 }}{5}\end{array}\)
Ta có: \(SA \bot (SBC) \Rightarrow SA \bot SH \Rightarrow \Delta SAH\)vuông tại S
Áp dụng hệ thức lượng trong \(\Delta SAH\) vuông tại S ta có:
\(A{H^2} = S{A^2} + S{H^2} = 9{a^2} + \frac{{4{a^2}}}{5} = \frac{{49{a^2}}}{5} \Rightarrow AH = \frac{{7a\sqrt 5 }}{5}\)
Đáp án B.
Tại một cuộc hội thảo quốc tế có 50 nhà khoa học trong đó có 31 người thành thạo tiếng Anh, 21 người thành thạo tiếng Pháp và 5 người thành thạo cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một người dự hội thảo. Xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là:
- A.\(\frac{{47}}{{50}}\)
- B.\(\frac{{37}}{{50}}\)
- C.\(\frac{{39}}{{50}}\)
- D.\(\frac{{41}}{{50}}\)
Đáp án : A
Sử dụng quy tắc cộng xác suất
Gọi A là biến cố “Người được chọn thành thạo tiếng Anh”; B là biến cố “Người được chọn thành thạo tiếng Pháp”.
Biến cố: “Người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc Pháp” là biến cố hợp của A và B.
Khi đó P(A) = \(P(A) = \frac{{31}}{{50}};P(B) = \frac{{21}}{{50}};P(AB) = \frac{5}{{50}} = \frac{1}{{10}}\)
Ta có: P(A ∪ B) = P(A) + P(B) – P(AB) = \(\frac{{31}}{{50}} + \frac{{21}}{{50}} - \frac{1}{{10}} = \frac{{47}}{{50}}\)
Vậy xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là \(\frac{{47}}{{50}}\)
Đáp án A.
Cho hàm số \(y = - {x^3} + 3x - 2\) có đồ thị \(\left( C \right).\)Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung là
- A.\(y = - 2x + 1\)
- B.\(y = 2x + 1\)
- C.\(y = 3x - 2\)
- D.\(y = - 3x - 2\)
Đáp án : C
Đạo hàm của hàm số\(y = f(x)\) tại điểm x0 là hệ số góc của tiếp tuyến với đồ thị (C) của hàm số tại điểm \({M_0}({x_0};f({x_0}))\)
Khi đó phương trình tiếp tuyến của (C) tại điểm M0 là: \(y = f'({x_0})(x - {x_0}) + f({x_0})\)
\(y' = \left( { - {x^3} + 3x - 2} \right)' = - 3{x^2} + 3\)
Giao điểm của \(\left( C \right)\) với trục tung là \(M(0; - 2)\)
Phương trình tiếp tuyến của \(\left( C \right)\) tại \(M(0; - 2)\) là: \(y = y'(0)(x - 0) + ( - 2) = 3x - 2\)
Đáp án C.
Cho hàm số \(y = {\sin ^2}x\). Khi đó đạo hàm y’ là
- A.\(y' = {\cos ^2}x\)
- B.\(y' = \sin 2x\)
- C.\(y' = \frac{{ - 3}}{{{{\sin }^2}x}} + 1\)
- D.\(y' = \frac{3}{{{{\sin }^2}x}}\)
Đáp án : B
Sử dụng công thức đạo hàm của hàm hợp.
\(y' = \left( {{{\sin }^2}x} \right)' = 2\sin x.c{\rm{os}}x = \sin 2x\)
Đáp án B.
Hàm số \(y = \sqrt {2 + 2{x^2}} \)có đạo hàm \(y' = \frac{{a + bx}}{{\sqrt {2 + 2{x^2}} }}\). Khi đó \(S = a - 2b\) có kết quả bằng
- A.\(S = - 4\)
- B.\(S = 10\)
- C.\(S = - 6\)
- D.\(S = 8\)
Đáp án : A
Sử dụng công thức đạo hàm của hàm hợp
\(\begin{array}{l}y' = \left( {\sqrt {2 + 2{x^2}} } \right)' = \frac{{\left( {2 + 2{x^2}} \right)'}}{{2\sqrt {2 + 2{x^2}} }} = \frac{{4x}}{{2\sqrt {2 + 2{x^2}} }} = \frac{{2x}}{{\sqrt {2 + 2{x^2}} }}\\ \Rightarrow a = 0,b = 2\\ \Rightarrow S = a - 2b = - 4\end{array}\)
Đáp án A.
Hàm số \(y = \frac{{{x^2} + x}}{{x - 1}}\)có đạo hàm \(y' = \frac{{a{x^2} + bx + c}}{{{{(x - 1)}^2}}}\). Khi đó \(S = a + b + c\) có kết quả là:
- A.1
- B.2
- C.5
- D.2
Đáp án : B
Sử dụng công thức đạo hàm của hàm hợp
\(\begin{array}{l}y' = \left( {\frac{{{x^2} + x}}{{x - 1}}} \right)' = \frac{{\left( {{x^2} + x} \right)'(x - 1) - ({x^2} + x)(x - 1)'}}{{{{(x - 1)}^2}}} = \frac{{(2x + 1)(x - 1) - ({x^2} + x)}}{{{{(x - 1)}^2}}} = \frac{{{x^2} - 2x - 1}}{{{{(x - 1)}^2}}}\\ \Rightarrow a = 1;b = - 2,c = - 1\\ \Rightarrow S = a + b + c = - 2\end{array}\)
Đáp án B.
Một chất điểm chuyển động có phương trình \(s\left( t \right) = {t^2} + 1\) (\(t\) tính bằng giây, \(s\) tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng
- A.\(1m/s.\)
- B.\(6m/s.\)
- C.\(4m/s.\)
- D.\(0m/s.\)
Đáp án : B
Phương trình vận tốc của chất điểm: \(v(t) = s'(t)\)
\(s'\left( t \right) = \left( {{t^2} + 1} \right)' = 2t\)
Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng \(v\left( 3 \right) = 2.3 = 6(m/s)\)
Đáp án B.
Hai người cùng bắn vào 1 bia. Người thứ nhất có xác suất bắn trúng là 60%, xác suất bắn trúng của người thứ 2 là 70%. Xác suất để cả hai người cùng bắn trật bằng
- A.
0,42
- B.
0,21
- C.
0,12
- D.
0,48
Đáp án : C
Sử dụng quy tắc nhân xác suất \(P(AB) = P(A).P(B)\).
Gọi A là biến cố "Người thứ nhất bắn trúng", B là biến cố "Người thứ hai bắn trúng".
Khi đó \(\overline{A}\) là biến cố "Người thứ nhất bắn trượt", \(\overline{B}\) là biến cố "Người thứ hai bắn trượt".
Ta có \(P(A) = 0,6\), \(P(B) = 0,7\) suy ra:
\(P\left( {\overline A } \right) = 1 - P\left( A \right) = 1 - 0,6 = 0,4\);
\(P\left( {\overline B } \right) = 1 - P\left( B \right) = 1 - 0,7 = 0,3\).
Vậy xác suất cả hai người bắn trượt là \(P\left( {\overline A \overline B } \right) = 0,4.0,3 = 0,12\).
Hàm số \(y = {x^5}\) có đạo hàm là:
- A.\(y' = 5{x^6}\)
- B.\(y' = 4{x^5}\)
- C.\(y' = 5x\)
- D.\(y' = 5{x^4}\)
Đáp án : D
Sử dụng công thức đạo hàm của hàm hợp
\(y' = \left( {{x^5}} \right)' = 5{x^4}\)
Đáp án D.
Một chất điểm chuyển động có phương trình chuyển động là \(s = s(t) = - {t^3} + 9{t^2} + t + 10\) (t được tính bằng giây, s được tính bẳng mét)
a) Đạo hàm của hàm số \(s(t)\) tại thời điểm \({t_0}\) là: \({t_0} + 4\)
b) Tính vận tốc tức thời của chuyển động tại thời điểm \(t = 5\)là \(16(m/s)\)
c) Tính gia tốc tức thời của chuyển động tại thời điểm \(t = 5\) là \(12(m/{s^2})\)
d) Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là t = 2 (s)
a) Đạo hàm của hàm số \(s(t)\) tại thời điểm \({t_0}\) là: \({t_0} + 4\)
b) Tính vận tốc tức thời của chuyển động tại thời điểm \(t = 5\)là \(16(m/s)\)
c) Tính gia tốc tức thời của chuyển động tại thời điểm \(t = 5\) là \(12(m/{s^2})\)
d) Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là t = 2 (s)
Phương trình vận tốc của chất điểm: \(v(t) = s'(t)\)
Phương trình gia tốc của chất điểm: \(a(t) = v'(t)\)
a) Đạo hàm của hàm số \(s(t)\)tại thời điểm \({t_0}\)
Ta có:
\(\begin{array}{l}f'({t_0}) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f(t) - f({t_0})}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to {t_0}} \left( {\frac{{{t^2} + 4t + 6 - ({t_0}^2 + 4{t_0} + 6)}}{{t - {t_0}}}} \right)\\ = \mathop {\lim }\limits_{t \to {t_0}} \left( {\frac{{(t - {t_0})(t + {t_0} + 4)}}{{t - {t_0}}}} \right) = \mathop {\lim }\limits_{t \to {t_0}} \left( {t + {t_0} + 4} \right) = 2{t_0} + 4\end{array}\)
b) Phương trình vận tốc của chất điểm là: \(v(t) = s' = s'(t) = \left( { - {t^3} + 9{t^2} + t + 10} \right)' = - 3{t^2} + 18t + 1\)
Vận tốc tức thời của chuyển động tại thời điểm t = 5 (s) là: \(v(5) = - {3.5^2} + 18.5 + 1 = 16\)
c) Phương trình gia tốc của chất điểm: \(a(t) = v'(t) = \left( { - 3{t^2} + 18t + 1} \right)' = - 6t + 18\)
Gia tốc tức thời của chuyển động tại thời điểm t = 5 (s) là: \(a(5) = - 6.5 + 18 = - 12(m/{s^2})\)
d) Phương trình vận tốc của chất điểm là: \(v(t) = s' = s'(t) = \left( { - {t^3} + 9{t^2} + t + 10} \right)' = - 3{t^2} + 18t + 1\)
Ta có: \(v(t) = - 3{t^2} + 18t + 1 = - 3{(t - 3)^2} + 24 \le 24\)
Vậy vận tốc đạt giá trị lớn nhất bằng 24 khi \(t - 3 = 0 \Leftrightarrow t = 3\)(s)
Cho hàm số có đồ thị (C): \(y = f(x) = \frac{{x + 1}}{{3x}}(C)\)
a) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Oy là: \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Ox là là\(y = - \frac{1}{3}x - \frac{1}{3}\)
c) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) tại giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là: \(y = - 3x + \frac{7}{3}\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = - \frac{1}{3}\) là \(y = - \frac{1}{3}x + 1\) và \(y = - \frac{1}{3}x - \frac{1}{3}\)
a) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Oy là: \(y = 9x - 2\)
b) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) với trục Ox là là\(y = - \frac{1}{3}x - \frac{1}{3}\)
c) Phương trình tiếp tuyến của (C) tại giao điểm của \((C)\) tại giao điểm của \((C)\) với đường thẳng \(y = x + 1\) là: \(y = - 3x + \frac{7}{3}\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = - \frac{1}{3}\) là \(y = - \frac{1}{3}x + 1\) và \(y = - \frac{1}{3}x - \frac{1}{3}\)
Bước 1: Gọi M(x0; f(x0)) là tọa độ tiếp điểm của tiếp tuyến của (C) thì f'(x0) = k
Bước 2: Giải phương trình f'(x0) = k với ẩn là x0.
Bước 3:Phương trình tiếp tuyến của (C) có dạng y = k(x – x0) + f(x0).
\(y' = f'(x) = \left( {\frac{{x + 1}}{{3x}}} \right)' = \frac{{ - 1}}{{3{x^2}}}\)
Cho tứ diện ABCD có tam giác ABC cân tại A, tam giác BCD cân tại D. Gọi I là trung điểm của cạnh BC. AH, IJ là đường cao tam giác AID.
a) \(BC \bot (AID)\)
b) \(AH \bot (BCD)\)
c) IJ là đường vuông góc chung của AD và BC
d) H là trọng tâm tam giác BCD
a) \(BC \bot (AID)\)
b) \(AH \bot (BCD)\)
c) IJ là đường vuông góc chung của AD và BC
d) H là trọng tâm tam giác BCD
Sử dụng định lý đường thẳng vuông góc với mặt phẳng
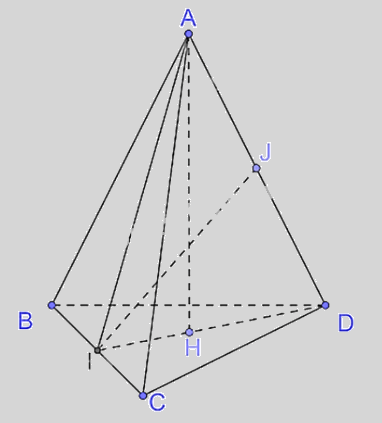
a) Vì tam giác ABC cân tại A, AI là trung tuyến nên AI đồng thời là đường cao hay AI \( \bot \)
Vì tam giác BCD cân tại D, DI là trung tuyến nên DI đồng thời là đường cao hay DI \( \bot \) BC.
Có AI \( \bot \)BC và DI \( \bot \) BC nên BC \( \bot \) (AID).
b) Do AH là đường cao của tam giác AID nên AH \( \bot \)
Vì BC \( \bot \) (AID) nên BC \( \bot \) AH mà AH\( \bot \)DI nên AH \( \bot \) (BCD).
c) Vì BC \( \bot \)(AID) nên BC \( \bot \)IJ, mà IJ là đường cao của tam giác AID nên IJ \( \bot \) Do đó IJ là đường vuông góc chung của AD và BC.
d) Tam giác BCD cân nên H không là trọng tâm tam giác BCD
Trong đợt kiểm tra cuối học kì II lớp 11 của các trường trung học phổ thông, thống kê cho thấy có 93% học sinh tỉnh X đạt yêu cầu; 87% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y. Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập
a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là\(0,7809\)
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là \(0,0091\)
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là \(0,1818\)
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là \(0,9909\)
a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là\(0,7809\)
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là \(0,0091\)
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là \(0,1818\)
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là \(0,9909\)
Sử dụng công thức nhân xác suất cho hai biến cố độc lập
Xác suất để học sinh tỉnh X không đạt yêu cầu là \(100\% - 93\% = 7\% = 0,07\)
Xác suất để học sinh tỉnh Y không đạt yêu cầu là \(100\% - 87\% = 13\% = 0,13\)
Gọi A là biến cố: “Học sinh tỉnh X đạt yêu cầu”
B là biến cố: “Học sinh tỉnh Y đạt yêu cầu”
Khi đó ta có: \(P(A) = 0,93;P(B) = 0,87;P(\overline A ) = 0,07;P(\overline B ) = 0,13\)
a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là:
\(P(AB) = P(A).P(B) = 0,93.0,87 = 0,8091\)
b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là
\(P(\overline {AB} ) = P(\overline A ).P(\overline B ) = 0,07.0,13 = 0,0091\)
c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là:
\(P(A\overline B ) + P(\overline A B) = 0,93.0,13 + 0,07.0,87 = 0,1818\)
d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là:
\(P(A \cup B) = P(A) + P(B) - P(AB) = 0,93 + 0,87 - 0,8091 = 0,9909\)
Tính giới hạn: \(I = \mathop {lim}\limits_{x \to - 3} \frac{{{x^2} + 2x - 3}}{{{x^2} + 5x + 6}}\)
Sử dụng phương pháp phân tích thành nhân tử
\(I = \mathop {lim}\limits_{x \to - 3} \frac{{{x^2} + 2x - 3}}{{{x^2} + 5x + 6}} = \mathop {lim}\limits_{x \to - 3} \frac{{(x + 3)(x - 1)}}{{(x + 3)(x + 2)}}\)
\( = \mathop {lim}\limits_{x \to - 3} \frac{{x - 1}}{{x + 2}} = 4\)
Cho hàm số : \(y = 5{x^4} - 3{x^3} + 6x - \sqrt 7 \). Tính \(f'\left( 0 \right)\).
Sử dụng công thức tính đạo hàm của hàm hợp
\(\begin{array}{l}y' = 20{x^3} - 9{x^2} + 6\\y'(0) = 6\end{array}\)
Cho hình chóp tứ giác đều\(S.ABCD\)có tất cả các cạnh bằng \(a\). Tính khoảng cách từ đỉnh \(S\) đến mặt phẳng \((ABCD).\)
\(d(S,(ABCD)) = SO\)
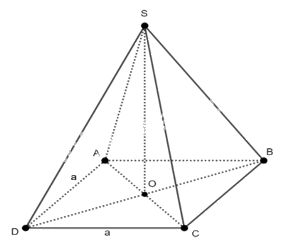
Gọi \(O\) là tâm của hình vuông \(ABCD.\) Suy ra \(SO \bot (ABCD)\) hay \(SO \bot BD\)
Xét hình vuông \(ABCD\) cạnh \(a,\) ta có \(AD = AB = a.\)
Suy ra \(BD = a\sqrt 2 \)(đường chéo hình vuông)\( \Rightarrow OD = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác vuông \(SDO\)vuông tại \(O,\) áp dụng định lý Pitago ta có: \(S{D^2} = S{O^2} + O{D^2} \Rightarrow S{O^2} = S{D^2} - O{D^2} = {a^2} - {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2} = \frac{{{a^2}}}{2} \Rightarrow SO = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d(S,(ABCD)) = SO = \frac{{a\sqrt 2 }}{2}.\)
Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\).Cạnh bên \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\sqrt 2 \).Góc giữa đường thẳng \(SC\)và mặt phẳng \(\left( {ABCD} \right)\)bằng
Sử dụng phương pháp xác định góc giữa đường thẳng và mặt phẳng
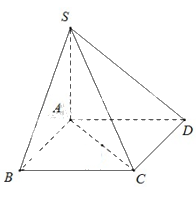
\(\left( {\widehat {SC,\left( {ABCD} \right)}} \right) = \left( {\widehat {SC,AC}} \right) = \widehat {SCA}\)
Tam giác \(SAC\) có \(SA \bot AC,SA = AC = a\sqrt 2 \) Suy ra \(\widehat {SCA} = {45^0}.\)
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^2} + c\) với \(a,b,c \in \mathbb{R}\). Biết rằng đồ thị hàm số đi qua hai điểm \(A\left( {1; - 3} \right)\) và \(B\left( {2;3} \right)\), đồng thời tiếp tuyến của đồ thị tại điểm có hoành độ bằng \( - 1\) có hệ số góc bằng 2. Tính tổng \(S = a + b + c\).
Viết phương trình hàm số biết đồ thị hàm số đi qua A và B; đồng thời là tiếp tuyến có hoành độ bằng -1 có hệ số góc bằng 2.
Từ đó lập hệ phương trình 3 ẩn tương ứng
Đồ thị hàm số đi qua điểm \(A\left( {1; - 3} \right)\) nên \( - 3 = a + b + c\) \(\left( 1 \right)\)
Đồ thị hàm số đi qua điểm \(B\left( {2;3} \right)\) nên \(16a + 4b + c = 3\) \(\left( 2 \right)\)
Tiếp tuyến của đồ thị tại điểm có hoành độ bằng \( - 1\) có hệ số góc bằng 2 nên \(f'\left( { - 1} \right) = 2 \Leftrightarrow - 4a - 2b = - 2 \Leftrightarrow 2a + b = 1\) \(\left( 3 \right)\)
Từ \(\left( 1 \right)\), \(\left( 2 \right)\), \(\left( 3 \right)\) ta có hệ phương trình:
\(\left\{ \begin{array}{l}a + b + c = - 3\\16a + 4b + c = 3\\2a + b = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 3\\c = - 1\end{array} \right.\)
Vậy \(S = -3\).
Cho hàm số \(y = \frac{{x - 2}}{{x + 3}}\) có đồ thị \(\left( C \right).\) Tìm điểm \(M\) trên đồ thị \(\left( C \right)\) sao cho tiếp tuyến của \(\left( C \right)\) tại \(M\)tạo với hai trục tọa độ một tam giác có diện tích bằng \(\frac{{18}}{5}.\)
Gọi tọa độ điểm M thuộc \(\left( C \right)\). Lập phương trình tính diện tích tam giác
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 3} \right\}\)
Gọi \(M\left( {a;\frac{{a - 2}}{{a + 3}}} \right) \in \left( C \right)\).
\(y' = \frac{5}{{{{\left( {x + 3} \right)}^2}}}\)
Phương trình tiếp tuyến của \(\left( C \right)\) tại \(M\): \(y = \frac{5}{{{{\left( {a + 3} \right)}^2}}}\left( {x - a} \right) + \frac{{a - 2}}{{a + 3}}{\rm{ }}\left( \Delta \right)\)
\(A = Ox \cap \Delta \Rightarrow A\left( {\frac{{ - {a^2} + 4a + 6}}{5};0} \right)\)
\(B = Oy \cap \Delta \Rightarrow B\left( {0;\frac{{{a^2} - 4a - 6}}{{{{\left( {a + 3} \right)}^2}}}} \right)\)
\(\begin{array}{l}{S_{OAB}} = \frac{1}{2}OA.OB \Leftrightarrow \frac{1}{2}\left| {\frac{{ - {a^2} + 4a + 6}}{5}} \right|.\left| {\frac{{{a^2} - 4a - 6}}{{{{\left( {a + 3} \right)}^2}}}} \right| = \frac{{18}}{5}\\ \Leftrightarrow {\left( {{a^2} - 4a - 6} \right)^2} = 36{\left( {a + 3} \right)^2}\\ \Leftrightarrow \left[ \begin{array}{l}{a^2} - 10a - 24 = 0\\{a^2} + 2a + 12 = 0:vn\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 12\\a = - 2\end{array} \right.\end{array}\)
Vậy \(M\left( {12;\frac{2}{3}} \right)\) hoặc \(M\left( { - 2; - 4} \right).\)
Đề thi học kì 2 Toán 11 - Đề số 4: Tổng quan và Hướng dẫn Luyện thi
Học kì 2 môn Toán lớp 11 là giai đoạn quan trọng, củng cố kiến thức nền tảng cho các năm học tiếp theo và chuẩn bị cho kỳ thi THPT Quốc gia. Việc luyện tập thông qua các đề thi là phương pháp hiệu quả nhất để nắm vững kiến thức và rèn luyện kỹ năng giải đề. Bài viết này sẽ cung cấp thông tin chi tiết về Đề thi học kì 2 Toán 11 - Đề số 4 của tusach.vn, cùng với những lời khuyên hữu ích để bạn đạt kết quả tốt nhất.
Nội dung Đề thi học kì 2 Toán 11 - Đề số 4
Đề thi này bao gồm các chủ đề chính sau:
- Hàm số lượng giác: Các dạng bài tập về xét tính đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác.
- Phương trình lượng giác: Giải các phương trình lượng giác cơ bản và nâng cao, sử dụng các công thức lượng giác.
- Đạo hàm: Tính đạo hàm của hàm số, ứng dụng đạo hàm để giải các bài toán về cực trị, khoảng đơn điệu.
- Tích phân: Tính tích phân xác định, ứng dụng tích phân để tính diện tích hình phẳng.
- Số phức: Các phép toán trên số phức, phương trình bậc hai với hệ số thực.
Cấu trúc Đề thi học kì 2 Toán 11 - Đề số 4
Đề thi được chia thành hai phần chính:
- Phần trắc nghiệm: Khoảng 20 câu hỏi, tập trung vào các kiến thức cơ bản và khả năng nhận biết.
- Phần tự luận: Khoảng 3-5 câu hỏi, yêu cầu học sinh trình bày lời giải chi tiết và vận dụng kiến thức vào giải quyết vấn đề.
Tại sao nên luyện thi với Đề thi học kì 2 Toán 11 - Đề số 4 của tusach.vn?
- Đề thi được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm: Đảm bảo tính chính xác và phù hợp với chương trình học.
- Đáp án chi tiết và dễ hiểu: Giúp học sinh tự đánh giá kết quả và rút kinh nghiệm.
- Đa dạng các dạng bài tập: Rèn luyện kỹ năng giải đề và khả năng tư duy logic.
- Giao diện thân thiện và dễ sử dụng: Tạo cảm giác thoải mái cho học sinh trong quá trình luyện thi.
Lời khuyên khi luyện thi học kì 2 Toán 11
Để đạt kết quả tốt nhất trong kỳ thi học kì 2 môn Toán lớp 11, bạn nên:
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép bài giảng và làm bài tập đầy đủ.
- Luyện tập thường xuyên: Giải nhiều đề thi khác nhau để làm quen với các dạng bài tập và rèn luyện kỹ năng giải đề.
- Tìm kiếm sự giúp đỡ khi cần thiết: Hỏi thầy cô giáo, bạn bè hoặc tham gia các diễn đàn học tập trực tuyến.
- Giữ tinh thần thoải mái: Đừng quá căng thẳng, hãy dành thời gian nghỉ ngơi và thư giãn.
Bảng so sánh các đề thi học kì 2 Toán 11 tại tusach.vn
| Đề số | Độ khó | Thời gian làm bài | Số câu hỏi |
|---|---|---|---|
| Đề số 1 | Dễ | 60 phút | 50 |
| Đề số 2 | Trung bình | 90 phút | 60 |
| Đề số 3 | Khó | 90 phút | 60 |
| Đề số 4 | Trung bình - Khó | 90 phút | 60 |
Đề thi học kì 2 Toán 11 - Đề số 4 là một công cụ hữu ích giúp bạn chuẩn bị tốt nhất cho kỳ thi sắp tới. Hãy truy cập tusach.vn ngay hôm nay để tải đề thi và bắt đầu luyện tập!