Đề thi học kì 2 Toán 11 - Đề số 3
Tổng quan nội dung
Đề thi học kì 2 Toán 11 - Đề số 3
Chào mừng bạn đến với Đề thi học kì 2 Toán 11 - Đề số 3 tại tusach.vn. Đề thi này được biên soạn theo cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo, giúp bạn làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các câu hỏi trắc nghiệm và tự luận, tập trung vào các kiến thức trọng tâm của chương trình Toán 11 học kì 2. Đáp án chi tiết đi kèm sẽ giúp bạn tự đánh giá kết quả và rút kinh nghiệm.
Đề bài
Đạo hàm của hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^3} + 2{x^2} + x + 4} - 2}}{{x + 1}}{\rm{ khi }}x \ne - 1\\0{\rm{ khi }}x = - 1\end{array} \right.\) tại \(x = - 1\) là:
- A.0
- B.Không tồn tại.
- C.
\( - \frac{1}{4}\)
- D.
\(\frac{1}{2}\)
Đạo hàm của hàm số \(y = \sqrt {4{x^2} + 3x + 1} \) là hàm số nào sau đây?
- A.
\(y = 12x + 3\).
- B.
\(y = \frac{{8x + 3}}{{\sqrt {4{x^2} + 3x + 1} }}\).
- C.
\(y = \frac{1}{{2\sqrt {4{x^2} + 3x + 1} }}\).
- D.
\(y = \frac{{8x + 3}}{{2\sqrt {4{x^2} + 3x + 1} }}\).
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) với \(a,b,c,d \in R\);\(a > 0\) và \(\left\{ \begin{array}{l}d > 2021\\a + b + c + d - 2021 < 0\end{array} \right.\). Hỏi phương trình \(f\left( x \right) - 2021 = 0\) có mấy nghiệm phân biệt?
- A.0
- B.3
- C.2
- D.1
Cho hình chóp S.ABC có SA ⊥ (ABC) và ΔABC vuông ở B. AH là đường cao của ΔSAB. Khẳng định nào sau đây sai ?
- A.
\(SA \bot BC\)
- B.
\(AH \bot BC\)
- C.
\(AH \bot AC\)
- D.
\(AH \bot SC\)
Cho hàm số \(y = \frac{{x - 1}}{{x - 2}}\), tiếp tuyến tại giao điểm của đồ thị hàm số với trục hoành có phương trình là:
- A.\(y = - x + 1\)
- B.\(y = - x + 2\)
- C.\(y = - 2x + 1\)
- D.\(y = - x - 1\)
Trong không gian, cho \(\alpha \) là góc giữa 2 mặt phẳng (P) và (Q) nào đó. Hỏi góc \(\alpha \) thuộc đoạn nào?
- A.\(\left[ {{0^0};{{90}^0}} \right]\)
- B.\(\left[ {{0^0};{{180}^0}} \right]\)
- C.\(\left[ {{{90}^0};{{180}^0}} \right]\)
- D.\(\left[ { - {{90}^0};{{90}^0}} \right]\)
Cho hàm số \(f(x) = \frac{{2x - 3}}{{x - 1}}\) , các mệnh đề sau, mệnh đề nào sai?
- A.Hàm số liên tục tại \(x = 2\)
- B.Hàm số liên tục tại \(x = 3\)
- C.Hàm số liên tục tại \(x = 1\)
- D.Hàm số liên tục tại \(x = - 1\)
Biết rằng \(\mathop {\lim }\limits_{x \to 2} \left( {{x^2} - 2x + m + 1} \right) = 11\). Hỏi m thuộc khoảng nào trong các khoảng sau?
- A.\(\left( {12;18} \right)\)
- B.\(\left( {9;12} \right)\)
- C.\(\left( {5;8} \right)\)
- D.\(\left( {8;10} \right)\)
Cho hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}} - \cos x - 2x\). Bất phương trình \(y' < 0\) có tập nghiệm T là :
- A.\(T = \left( {0;\frac{\pi }{2}} \right)\)
- B.\(T = \left( {\frac{\pi }{2};2\pi } \right)\)
- C.\(T = \left( { - 2\pi ;2\pi } \right)\)
- D.\(T = R\)
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình vuông. Hỏi mp(SCD) vuông góc với mặt phẳng nào trong các mặt phẳng sau ?
- A.\(mp\left( {SBD} \right)\)
- B.\(mp\left( {SAC} \right)\)
- C.\(mp\left( {SAB} \right)\)
- D.\(mp\left( {SAD} \right)\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy ABCD và C. Hỏi khoảng cách từ điểm A tới mặt phẳng (SBC) bằng:
- A.\(\frac{{a\sqrt 3 }}{3}\)
- B.\(\frac{{a\sqrt 3 }}{2}\)
- C.\(\frac{{a\sqrt 3 }}{4}\)
- D.\(\frac{{a\sqrt 2 }}{2}\)
Cho hình chóp tứ giác đều S.ABCD. Đáy ABCD là hình vuông tâm O, gọi I là trung điểm của cạnh AD. Hỏi góc giữa 2 mặt phẳng (SAD) và (ABCD) là:
- A.\(\widehat {SIO}\)
- B.\(\widehat {SOI}\)
- C.\(\widehat {OSI}\)
- D.\(\widehat {SAO}\)
Một chất điểm chuyển động có phương trình chuyển động là \(s = s(t) = 2{t^2} + t - 1\) (t được tính bằng giây, s được tính bẳng mét)
a) Đạo hàm của hàm số \(s(t)\) tại thời điểm \({t_0}\) là: \({t_0} + 4\)
b) Vận tốc tức thời của chuyển động tại thời điểm \(t = 2\)là \(9\,(m/s)\)
c) Vận tốc tức thời của chuyển động tại thời điểm \(t = 5\) là 12 \((m/s)\)
d) Vận tốc trung bình của chất điểm trong khoảng thời gian từ \(t = 0\) tới \(t = 2s\)là 5 (m/s)
Cho hàm số có đồ thị (C): \(y = f(x) = {x^2} + 2x - 4(C)\)
a) Hệ số góc của tiếp tuyến của \((C)\) tại điểm có hoành độ \({x_0} = 1\) thuộc \((C)\) là k = 2
b) Phương trình tiếp tuyến của (C) tại điểm có hoành độ \({x_0} = 0\) thuộc \((C)\) là \(y = 2x - 4\)
c) Phương trình tiếp tuyến của (C) tại điểm có tung độ \({y_0} = - 1\) là: \(y = 4x - 5\) hoặc \(y = - 4x - 13\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = - 4\) là \(y = - 4x - 13\)
Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SA vuông góc với đáy. Gọi H, I, K lần lượt là hình chiếu vuông góc của A lên SB, SC, SD
a) \(CD \bot (SAD)\)
b) \(SC \bot (SAC)\)
c) \(SC \bot HK\)
d) \(HK \bot AI\)
Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần.
a) Không gian mẫu là Ω = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6)}.
b) Số phần tử của biến cố A: "Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10" là n(A) = 6 và số phần tử của biến cố B: "Mặt 5 chấm xuất hiện ít nhất một lần" là n(B) = 11.
c) Xác suất của biến cố A là \(P(A) = \frac{1}{6}\).
d) Xác suất của biến cố B là \(P(B) = \frac{5}{{36}}\).
Tính giới hạn: \(I = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2x}}{{{x^2} - 3x + 2}}\)
Cho hàm số : \(f\left( x \right) = {\sin ^3}\left( {\frac{\pi }{3} - 2x} \right)\). Tính \(f'\left( {\frac{\pi }{3}} \right)\).
Sau khi đỗ Đại học bạn Nam được bố mua cho chiếc xe máy để sử dụng. Xe có giá trị ban đầu là 20 triệu, sau mỗi năm giá trị xe giảm 10% so với năm trước đó. Hỏi sau bao nhiêu năm thì giá trị của xe còn lại là 12 triệu.
Tìm a để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^3} - 2{x^2} + 3x - 2}}{{x - 1}};\,\,khi\,x \ne 1\\2x + a\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 1\end{array} \right.\)liên tục trên R
Cho hình chóp \(S.ABC\) có cạnh bên \(SA\) vuông góc với mặt phẳng \((ABC)\) và \(ABC\) là tam giác đều cạnh bằng \(a.\) Biết khoảng cách từ điểm \(A\) đến mặt phẳng \((SBC)\) bàng \(a\sqrt {\frac{6}{{11}}} \) . Tính thể tích khối chóp \(S.ABC\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B.\) Biết \(AD = 2a,\,AB = BC = SA = a.\) Cạnh bên \(SA\) vuông góc với mặt đáy, gọi \(M\) là trung điểm của \(AD.\) Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {SCD} \right)\) theo \(a.\)
Lời giải và đáp án
Đạo hàm của hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{\sqrt {{x^3} + 2{x^2} + x + 4} - 2}}{{x + 1}}{\rm{ khi }}x \ne - 1\\0{\rm{ khi }}x = - 1\end{array} \right.\) tại \(x = - 1\) là:
- A.0
- B.Không tồn tại.
- C.
\( - \frac{1}{4}\)
- D.
\(\frac{1}{2}\)
Đáp án : C
Sử dụng Định nghĩa đạo hàm :
\(f'({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}\) hoặc \(f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}\)
\(\begin{array}{l}f'( - 1) = \mathop {\lim }\limits_{x \to - 1} \frac{{f(x) - f( - 1)}}{{x - ( - 1)}} = \mathop {\lim }\limits_{x \to - 1} \frac{{\frac{{\sqrt {{x^3} + 2{x^2} + x + 4} - 2}}{{x + 1}} - 0}}{{x + 1}} = \mathop {\lim }\limits_{x \to - 1} \frac{{\sqrt {{x^3} + 2{x^2} + x + 4} - 2}}{{{{\left( {x + 1} \right)}^2}}}\\ = \mathop {\lim }\limits_{x \to - 1} \frac{{{x^3} + 2{x^2} + x + 4 - 4}}{{{{\left( {x + 1} \right)}^2}(\sqrt {{x^3} + 2{x^2} + x + 4} + 2)}} = \mathop {\lim }\limits_{x \to - 1} \frac{{{x^3} + 2{x^2} + x}}{{{{\left( {x + 1} \right)}^2}(\sqrt {{x^3} + 2{x^2} + x + 4} + 2)}}\\ = \mathop {\lim }\limits_{x \to - 1} \frac{{x({x^2} + 2x + 1)}}{{{{\left( {x + 1} \right)}^2}(\sqrt {{x^3} + 2{x^2} + x + 4} + 2)}} = \mathop {\lim }\limits_{x \to - 1} \frac{x}{{\sqrt {{x^3} + 2{x^2} + x + 4} + 2}} = \frac{{ - 1}}{4}\end{array}\)
Đáp án C.
Đạo hàm của hàm số \(y = \sqrt {4{x^2} + 3x + 1} \) là hàm số nào sau đây?
- A.
\(y = 12x + 3\).
- B.
\(y = \frac{{8x + 3}}{{\sqrt {4{x^2} + 3x + 1} }}\).
- C.
\(y = \frac{1}{{2\sqrt {4{x^2} + 3x + 1} }}\).
- D.
\(y = \frac{{8x + 3}}{{2\sqrt {4{x^2} + 3x + 1} }}\).
Đáp án : D
Sử dụng công thức tính đạo hàm của hàm hợp\(y' = \left( {\sqrt u } \right)' = \frac{{u'}}{{2\sqrt u }}\)
\(y' = \left( {\sqrt {4{x^2} + 3x + 1} } \right)' = \frac{{\left( {4{x^2} + 3x + 1} \right)'}}{{2\sqrt {4{x^2} + 3x + 1} }} = \frac{{8x + 3}}{{2\sqrt {4{x^2} + 3x + 1} }}\)
Đáp án D.
Cho hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) với \(a,b,c,d \in R\);\(a > 0\) và \(\left\{ \begin{array}{l}d > 2021\\a + b + c + d - 2021 < 0\end{array} \right.\). Hỏi phương trình \(f\left( x \right) - 2021 = 0\) có mấy nghiệm phân biệt?
- A.0
- B.3
- C.2
- D.1
Đáp án : B
Sử dụng ứng dụng tính liên tục của hàm số trong chứng minh phương trình có nghiệm
\(\begin{array}{l}g(x) = f(x) - 2021 = a{x^3} + b{x^2} + cx + d - 2021\\g(0) = d - 2021 > 0\\g(1) = a + b + c + d - 2021 < 0\end{array}\)
Ta có: \(\mathop {\lim }\limits_{x \to \infty } \left( {a{x^3} + b{x^2} + cx + d - 2021} \right) = + \infty \)
Suy ra, tồn tại giá trị \({x_1} > 1\) sao cho \(g\left( {{x_1}} \right) > 0\)
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } \left( {a{x^3} + b{x^2} + cx + d - 2021} \right) = - \infty \)
Suy ra, tồn tại \({x_2} < 0\) sao cho \(g\left( {{x_2}} \right) > 0\)
Ta có: \(\left\{ \begin{array}{l}g\left( {{x_1}} \right).g(1) < 0\\g(0).g(1) < 0\\g\left( {{x_2}} \right).g(0) < 0\end{array} \right.\)
Suy ra, \(g\left( x \right) = 0\) có ba nghiệm phân biệt
Đáp án B.
Cho hình chóp S.ABC có SA ⊥ (ABC) và ΔABC vuông ở B. AH là đường cao của ΔSAB. Khẳng định nào sau đây sai ?
- A.
\(SA \bot BC\)
- B.
\(AH \bot BC\)
- C.
\(AH \bot AC\)
- D.
\(AH \bot SC\)
Đáp án : C
Sử dụng định lý đường vuông góc với mặt phẳng
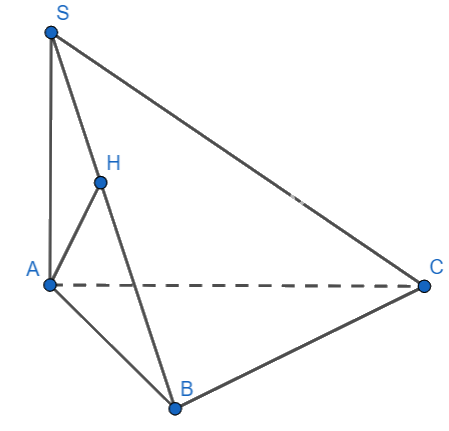
Đáp án B,D.
Ta có: \(\left\{ \begin{array}{l}BC \bot BA\\BC \bot SA\\SA,BA \subset (SAB)\\SA \cap BA\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AH\)
Mặt khác:
\(\begin{array}{l}\left\{ \begin{array}{l}AH \bot BC\\AH \bot SB\\SB,BC \subset (SBC)\\SB \cap BC\end{array} \right. \Rightarrow AH \bot (SBC)\\ \Rightarrow AH \bot BC;\,AH \bot SC\end{array}\)
Đáp án A: \(SA \bot (ABCD) \Rightarrow SA \bot BC\)
Đáp án C.
Cho hàm số \(y = \frac{{x - 1}}{{x - 2}}\), tiếp tuyến tại giao điểm của đồ thị hàm số với trục hoành có phương trình là:
- A.\(y = - x + 1\)
- B.\(y = - x + 2\)
- C.\(y = - 2x + 1\)
- D.\(y = - x - 1\)
Đáp án : A
Phương trình tiếp tuyến tại điểm \(M({x_0},f({x_0}))\) là:\(y = f'({x_0})(x - {x_0}) + f({x_0})\)
Giao điểm của đồ thị hàm số với trục hoành là \(M(1;0)\)
\(\begin{array}{l}y' = \left( {\frac{{x - 1}}{{x - 2}}} \right)' = \frac{{ - 1}}{{{{\left( {x - 2} \right)}^2}}}\\y'(1) = - 1\end{array}\)
Phương trình tiếp tuyến của đồ thị hàm số tại điểm M là:
\(\begin{array}{l}y = f'(1)(x - 1) + 0 = - 1(x - 1) + 0\\y = - x + 1\end{array}\)
Đáp án A.
Trong không gian, cho \(\alpha \) là góc giữa 2 mặt phẳng (P) và (Q) nào đó. Hỏi góc \(\alpha \) thuộc đoạn nào?
- A.\(\left[ {{0^0};{{90}^0}} \right]\)
- B.\(\left[ {{0^0};{{180}^0}} \right]\)
- C.\(\left[ {{{90}^0};{{180}^0}} \right]\)
- D.\(\left[ { - {{90}^0};{{90}^0}} \right]\)
Đáp án : A
Dựa trên lý thuyết về góc giữa hai mặt phẳng và góc giữa hai đường thẳng:
1. Cho hai mặt phẳng (P) và (Q). Lấy các đường thẳng a, b tương ứng vuông góc với (P) và (Q). Khi đó, góc giữa a và b không phụ thuộc vào vị trí của a và b và được gọi là góc giữa hai mặt phẳng (P) và (Q).
2. Với hai đường thẳng a, b bất kỳ: \({0^0} \le \left( {a,b} \right) \le {90^0}\)
Góc \(\alpha \in \left[ {{0^0};{{90}^0}} \right]\)
Đáp án A.
Cho hàm số \(f(x) = \frac{{2x - 3}}{{x - 1}}\) , các mệnh đề sau, mệnh đề nào sai?
- A.Hàm số liên tục tại \(x = 2\)
- B.Hàm số liên tục tại \(x = 3\)
- C.Hàm số liên tục tại \(x = 1\)
- D.Hàm số liên tục tại \(x = - 1\)
Đáp án : C
1.Hàm số \(y = f(x)\)xác định trên \(K,{x_0} \in K\). Khi đó, \(y = f(x)\)liên tục tại \({x_0}\)khi \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\)
2. Hàm số \(y = f(x)\)gián đoạn (không liên tục) tại điểm \({x_0}\)khi tồn tại 1 điểm \({x_0}\)làm cho hàm số \(f({x_0})\) không liên tục.
Hàm số \(f(x) = \frac{{2x - 3}}{{x - 1}}\) xác định trên \(R\backslash \left\{ 1 \right\}\)
Nên hàm số không liên tục tại \(x = 1\)
Đáp án C.
Biết rằng \(\mathop {\lim }\limits_{x \to 2} \left( {{x^2} - 2x + m + 1} \right) = 11\). Hỏi m thuộc khoảng nào trong các khoảng sau?
- A.\(\left( {12;18} \right)\)
- B.\(\left( {9;12} \right)\)
- C.\(\left( {5;8} \right)\)
- D.\(\left( {8;10} \right)\)
Đáp án : B
Tính \(\mathop {\lim }\limits_{x \to 2} \left( {{x^2} - 2x + m + 1} \right)\) theo m
\(\mathop {\lim }\limits_{x \to 2} \left( {{x^2} - 2x + m + 1} \right) = {2^2} - 2.2 + m + 1 = m + 1\)
Ta có: \(\mathop {\lim }\limits_{x \to 2} \left( {{x^2} - 2x + m + 1} \right) = 11\) nên \(m + 1 = 11 \Leftrightarrow m = 10\)
Đáp án B.
Cho hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}} - \cos x - 2x\). Bất phương trình \(y' < 0\) có tập nghiệm T là :
- A.\(T = \left( {0;\frac{\pi }{2}} \right)\)
- B.\(T = \left( {\frac{\pi }{2};2\pi } \right)\)
- C.\(T = \left( { - 2\pi ;2\pi } \right)\)
- D.\(T = R\)
Đáp án : D
Sử dụng công thức đạo hàm của hàm lượng giác và hàm hợp
\(\begin{array}{l}y' = \left( {{\mathop{\rm s}\nolimits} {\rm{in}}x - \cos x - 2x} \right)' = \cos x + \sin x - 2 < 0\\ \Leftrightarrow \sqrt 2 \sin (x + \frac{\pi }{4}) - 2 < 0\\ \Leftrightarrow \sin (x + \frac{\pi }{4}) < \sqrt 2 \end{array}\)
Mặt khác, do \( - 1 \le \sin (x + \frac{\pi }{4}) \le 1,\forall x \in R\) nên \(\sin (x + \frac{\pi }{4}) < \sqrt 2 \) đúng \(\forall x \in R\)
Vậy BPT nghiệm đúng \(\forall x \in R\)
Đáp án D.
Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình vuông. Hỏi mp(SCD) vuông góc với mặt phẳng nào trong các mặt phẳng sau ?
- A.\(mp\left( {SBD} \right)\)
- B.\(mp\left( {SAC} \right)\)
- C.\(mp\left( {SAB} \right)\)
- D.\(mp\left( {SAD} \right)\)
Đáp án : D
Sử dụng định lý hai mặt phẳng vuông góc với nhau
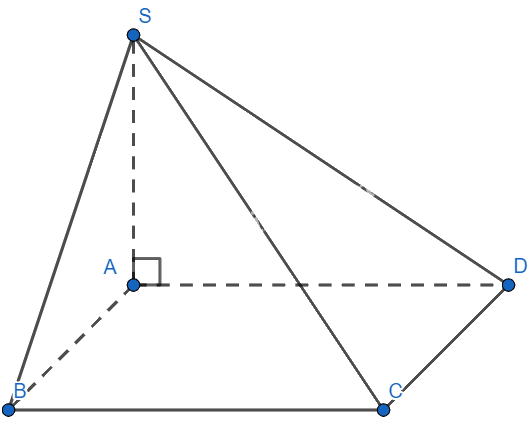
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\\SA,AD \subset (SAD)\\SA \cap AD\end{array} \right. \Rightarrow CD \bot (SAD)\\CD \subset (SCD) \Rightarrow (SCD) \bot (SAD)\end{array}\)
Đáp án D.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt đáy ABCD và C. Hỏi khoảng cách từ điểm A tới mặt phẳng (SBC) bằng:
- A.\(\frac{{a\sqrt 3 }}{3}\)
- B.\(\frac{{a\sqrt 3 }}{2}\)
- C.\(\frac{{a\sqrt 3 }}{4}\)
- D.\(\frac{{a\sqrt 2 }}{2}\)
Đáp án : B
Hạ \(AH \bot SB \Rightarrow d(A,(SBC)) = AH\)
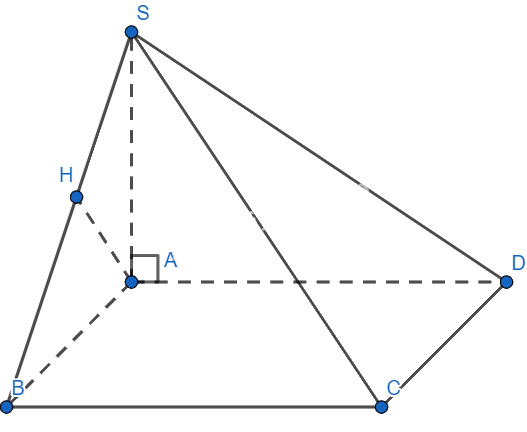
Ta có:
\(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\\AB,SA \subset (SAB)\\AB \cap SA\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot AH\)
Mặt khác,
\(\begin{array}{l}\left\{ \begin{array}{l}AH \bot SB\\AH \bot BC\\SB,BC \subset (SBC)\\SB \cap BC\end{array} \right. \Rightarrow AH \bot (SBC)\\ \Rightarrow d(AH,(SBC)) = AH\end{array}\)
Xét tam giác SAB vuông tại A ta có :
\(AH = \frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{a\sqrt 3 .a}}{{\sqrt {{{(a\sqrt 3 )}^2} + {a^2}} }} = \frac{{a\sqrt 3 }}{2} \Rightarrow d(AH,(SBC)) = \frac{{a\sqrt 3 }}{2}\)
Đáp án B.
Cho hình chóp tứ giác đều S.ABCD. Đáy ABCD là hình vuông tâm O, gọi I là trung điểm của cạnh AD. Hỏi góc giữa 2 mặt phẳng (SAD) và (ABCD) là:
- A.\(\widehat {SIO}\)
- B.\(\widehat {SOI}\)
- C.\(\widehat {OSI}\)
- D.\(\widehat {SAO}\)
Đáp án : B
Sử dụng phương tính xác định góc giữa hai mặt phẳng
Xét tam giác ADC có: OI là đường trung bình
Suy ra: \(OI//CD\) (tính chất đường trung bình)
Do ABCD là hình vuông nên \(CD \bot AD\)
Suy ra: \(OI \bot AD\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}AD \bot OI - cmt\\AD \bot SO\,\,(SO \bot (ABCD))\\OI,SO \subset (SOI)\\OI \cap SO\end{array} \right. \Rightarrow AD \bot (SOI)\\ \Rightarrow AD \bot SI\end{array}\)
Ta có:
\(\left\{ \begin{array}{l}(SAD) \cap (ABCD) = AD\\SI \subset (SAD),SI \bot AD\\OI \subset (ABCD),OI \bot AD\end{array} \right. \Rightarrow \left( {(SAD),(ABCD)} \right) = (SI,OI)\)
Xét tam giác SOI vuông tại O: \((SI,OI) = \widehat {SOI}\)
Đáp án B.
Một chất điểm chuyển động có phương trình chuyển động là \(s = s(t) = 2{t^2} + t - 1\) (t được tính bằng giây, s được tính bẳng mét)
a) Đạo hàm của hàm số \(s(t)\) tại thời điểm \({t_0}\) là: \({t_0} + 4\)
b) Vận tốc tức thời của chuyển động tại thời điểm \(t = 2\)là \(9\,(m/s)\)
c) Vận tốc tức thời của chuyển động tại thời điểm \(t = 5\) là 12 \((m/s)\)
d) Vận tốc trung bình của chất điểm trong khoảng thời gian từ \(t = 0\) tới \(t = 2s\)là 5 (m/s)
a) Đạo hàm của hàm số \(s(t)\) tại thời điểm \({t_0}\) là: \({t_0} + 4\)
b) Vận tốc tức thời của chuyển động tại thời điểm \(t = 2\)là \(9\,(m/s)\)
c) Vận tốc tức thời của chuyển động tại thời điểm \(t = 5\) là 12 \((m/s)\)
d) Vận tốc trung bình của chất điểm trong khoảng thời gian từ \(t = 0\) tới \(t = 2s\)là 5 (m/s)
Phương trình vận tốc của chất điểm: \(v(t) = s'(t)\)
Phương trình gia tốc của chất điểm: \(a(t) = v'(t)\)
a) Đạo hàm của hàm số \(s(t)\)tại thời điểm \({t_0}\)
Ta có:
\(\begin{array}{l}f'({t_0}) = \mathop {\lim }\limits_{t \to {t_0}} \frac{{f(t) - f({t_0})}}{{t - {t_0}}} = \mathop {\lim }\limits_{t \to {t_0}} \left( {\frac{{2{t^2} + t - 1 - (2{t_0}^2 + {t_0} - 1)}}{{t - {t_0}}}} \right)\\ = \mathop {\lim }\limits_{t \to {t_0}} \left( {\frac{{(t - {t_0})\left[ {2\left( {t + {t_0}} \right) + 1} \right]}}{{t - {t_0}}}} \right) = \mathop {\lim }\limits_{t \to {t_0}} \left[ {2\left( {t + {t_0}} \right) + 1} \right] = 4{t_0} + 1\end{array}\)
b) Phương trình vận tốc của chất điểm là: \(v(t) = s' = s'(t) = 4t + 1\)
Vận tốc tức thời của chuyển động tại thời điểm t = 2 (s) là: \(v(2) = 4.2 + 1 = 9\)\((m/s)\)
c) Vận tốc tức thời của chuyển động tại thời điểm t = 5 (s) là: \(v(5) = 4.5 + 1 = 21\)\((m/s)\)
d) Trong khoảng thời gian từ \(t = 0\) tới \(t = 2s\)thì chất điểm di chuyển được quãng đường: \(4.2 + 2 - 1 = 9(m)\)
Suy ra vận tốc trung bình của chất điểm trong khoảng thời gian 2s kể từ thời điểm \(t = 0\) là:
\(\overline v = \frac{{\Delta s}}{{\Delta t}} = \frac{{9 - 0}}{{2 - 0}} = 4,5(m/s)\)
Cho hàm số có đồ thị (C): \(y = f(x) = {x^2} + 2x - 4(C)\)
a) Hệ số góc của tiếp tuyến của \((C)\) tại điểm có hoành độ \({x_0} = 1\) thuộc \((C)\) là k = 2
b) Phương trình tiếp tuyến của (C) tại điểm có hoành độ \({x_0} = 0\) thuộc \((C)\) là \(y = 2x - 4\)
c) Phương trình tiếp tuyến của (C) tại điểm có tung độ \({y_0} = - 1\) là: \(y = 4x - 5\) hoặc \(y = - 4x - 13\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = - 4\) là \(y = - 4x - 13\)
a) Hệ số góc của tiếp tuyến của \((C)\) tại điểm có hoành độ \({x_0} = 1\) thuộc \((C)\) là k = 2
b) Phương trình tiếp tuyến của (C) tại điểm có hoành độ \({x_0} = 0\) thuộc \((C)\) là \(y = 2x - 4\)
c) Phương trình tiếp tuyến của (C) tại điểm có tung độ \({y_0} = - 1\) là: \(y = 4x - 5\) hoặc \(y = - 4x - 13\)
d) Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến \(k = - 4\) là \(y = - 4x - 13\)
Bước 1: Gọi M(x0; f(x0)) là tọa độ tiếp điểm của tiếp tuyến của (C) thì f'(x0) = k
Bước 2: Giải phương trình f'(x0) = k với ẩn là x0.
Bước 3:Phương trình tiếp tuyến của (C) có dạng y = k(x – x0) + f(x0).
\(y' = f'(x) = \left( {{x^2} + 2x - 4} \right)' = 2x + 2\)
a) Hệ số góc của tiếp tuyến của \((C)\) tại điểm có hoành độ \({x_0} = 1\) là \(k = y'(1) = 4\)
b) Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ \({x_0} = 0\) thuộc \((C)\) là:
\(y = y'(0)(x - 0) + y(0) \Leftrightarrow y = 2x - 4\)
c) Với \({y_0} = - 1 \Rightarrow y = x_0^2 + 2{x_0} - 4 = - 1 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 1\\{x_0} = - 3\end{array} \right.\). Vậy có hai tiếp điểm thuộc \((C)\) có tung độ \({y_0} = - 1\) là \(\left( {1; - 1} \right)\) và \(\left( { - 3; - 1} \right)\). Nên ta có:
Phương trình tiếp tuyến tại điểm \(\left( {1; - 1} \right)\) là: \(y = y'(1)(x - 1) + y(1) \Leftrightarrow y = 4x - 5\)
Phương trình tiếp tuyến tại điểm \(\left( { - 3; - 1} \right)\) là: \(y = y'( - 3)(x + 3) + y( - 3) \Leftrightarrow y = - 4x - 13\)
d)Gọi \(M\left( {a;b} \right)\) là tiếp điểm của tiếp tuyến của đồ thị \((C)\) với hệ số góc \(k = - 4\)
\( \Rightarrow y'(a) = - 4 \Leftrightarrow 2a + 2 = - 4 \Leftrightarrow a = - 3 \Rightarrow b = - 1\)
Suy ra phương trình tiếp tuyến với hệ số góc \(k = - 4\) là \(y = - 4(x + 3) - 1 \Leftrightarrow y = - 4x - 13\)
Cho hình chóp S.ABCD có đáy là hình vuông tâm O và SA vuông góc với đáy. Gọi H, I, K lần lượt là hình chiếu vuông góc của A lên SB, SC, SD
a) \(CD \bot (SAD)\)
b) \(SC \bot (SAC)\)
c) \(SC \bot HK\)
d) \(HK \bot AI\)
a) \(CD \bot (SAD)\)
b) \(SC \bot (SAC)\)
c) \(SC \bot HK\)
d) \(HK \bot AI\)
Sử dụng định lý đường thẳng vuông góc với mặt phẳng
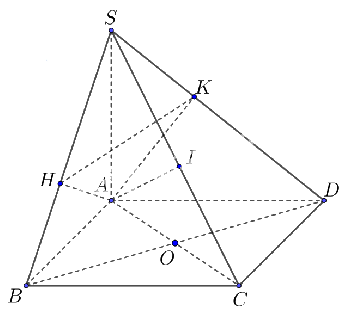
a) Do ABCD là hình vuông nên \(CD \bot AD \subset (SAD)(1)\)
\(SA \bot (ABCD) \Rightarrow SA \bot CD\,(2)\)
Trong (SAD): \(SA \cap AD = A,(3)\)
Từ (1), (2) và (3) nên \(CD \bot (SAD)\)
b) Do ABCD là hình vuông nên \(BD \bot AC\,(4)\)
\(SA \bot (ABCD);BD \subset (ABCD) \Rightarrow SA \bot BD\,\,(5)\)
Trong (SAC): \(SA \cap AC = A,(6)\)
Từ (4), (5) và (6) nên \(BD \bot (SAC)\)
c)Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\\AB,SA \subset (SAB)\end{array} \right. \Rightarrow BC \bot (SAB)\) mà \(AH \subset (SAB) \Rightarrow AH \bot BC\)
Lại có \(AH \bot SB\) nên theo hệ quả, ta được \(AH \bot SC\)
Theo câu (a), \(CD \bot (SAD)\) mà \(AK \subset (SAD)\) nên \(AK \bot CD\)
Lại có AK là đường cao của tam giác \(SAD \Rightarrow AK \bot SD\)
Nên theo hệ quả \(AK \bot SC\)
Trong tam giác AKH: \(AH \bot SC,AK \bot SC\) nên theo hệ quả \(HK \bot SC\)
d)Ta có: \(\Delta SAB = \Delta SAD\,(c.g.c) \Rightarrow \frac{{SH}}{{SB}} = \frac{{SK}}{{SD}} \Rightarrow HK//BD\,(7)\)
Theo câu (a), \(BD \bot (SAC)\) mà \(AI \subset (SAC) \Rightarrow BD \bot AI\,(8)\)
Từ (7) và (8), \(HK \bot AI\)
Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần.
a) Không gian mẫu là Ω = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6)}.
b) Số phần tử của biến cố A: "Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10" là n(A) = 6 và số phần tử của biến cố B: "Mặt 5 chấm xuất hiện ít nhất một lần" là n(B) = 11.
c) Xác suất của biến cố A là \(P(A) = \frac{1}{6}\).
d) Xác suất của biến cố B là \(P(B) = \frac{5}{{36}}\).
a) Không gian mẫu là Ω = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6)}.
b) Số phần tử của biến cố A: "Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10" là n(A) = 6 và số phần tử của biến cố B: "Mặt 5 chấm xuất hiện ít nhất một lần" là n(B) = 11.
c) Xác suất của biến cố A là \(P(A) = \frac{1}{6}\).
d) Xác suất của biến cố B là \(P(B) = \frac{5}{{36}}\).
Sử dụng các quy tắc tính xác suất của biến cố.
a) Sai. Phép thử T: "Gieo một con xúc xắc cân đối và đồng chất hai lần".
Ω = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}.
b) Đúng. A = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)} nên n(A) = 6.
B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)} nên n(B) = 11.
c) Đúng. \(P(A) = \frac{6}{{36}} = \frac{1}{6}\).
d) Sai. \(P(B) = \frac{{11}}{{36}}\).
Tính giới hạn: \(I = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2x}}{{{x^2} - 3x + 2}}\)
Sử dụng phương pháp nhân liên hợp và phân tích thành nhân tử
\(I = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3} - 2x}}{{{x^2} - 3x + 2}} = I = \mathop {\lim }\limits_{x \to 1} \frac{{x + 3 - 4{x^2}}}{{\left( {\sqrt {x + 3} + 2x} \right)\left( {x - 1} \right)\left( {x - 2} \right)}}\)
\(I = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x - 1} \right)\left( { - 4x - 3} \right)}}{{\left( {\sqrt {x + 3} + 2x} \right)\left( {x - 1} \right)\left( {x - 2} \right)}}\)
\(I = \mathop {\lim }\limits_{x \to 1} \frac{{\left( { - 4x - 3} \right)}}{{\left( {\sqrt {x + 3} + 2x} \right)\left( {x - 2} \right)}}\)
\(I = \frac{7}{4}\)
Cho hàm số : \(f\left( x \right) = {\sin ^3}\left( {\frac{\pi }{3} - 2x} \right)\). Tính \(f'\left( {\frac{\pi }{3}} \right)\).
Sử dụng công thức tính đạo hàm của hàm hợp
\(f'(x) = 3si{n^2}\left( {\frac{\pi }{3} - 2x} \right).cos\left( {\frac{\pi }{3} - 2x} \right).( - 2)\)
\(f'(x) = - 6si{n^2}\left( {\frac{\pi }{3} - 2x} \right).cos\left( {\frac{\pi }{3} - 2x} \right)\)
\(f'\left( {\frac{\pi }{3}} \right) = - \frac{9}{4}\)
Sau khi đỗ Đại học bạn Nam được bố mua cho chiếc xe máy để sử dụng. Xe có giá trị ban đầu là 20 triệu, sau mỗi năm giá trị xe giảm 10% so với năm trước đó. Hỏi sau bao nhiêu năm thì giá trị của xe còn lại là 12 triệu.
Gọi giá trị của xe năm thứ n là \({x_n} = 12.000.000\)đ, giá trị xe ban đầu là \({x_0} = 20.000.000\)đ và với hao mòn \(r = 10\% \)
Sau một năm giá trị của xe còn lại là: \({x_1} = {x_0} - r{x_0} = {x_0}(1 - r)\)
Sau hai năm, giá trị của còn lại là: \({x_2} = {x_1} - r{x_1} = {x_1}(1 - r) = {x_0}{(1 - r)^2}\)
Sau n năm, giá trị của xe còn lại là: \({x_n} = {x_{n - 1}} - r{x_{n - 1}} = {x_{n - 1}}(1 - r) = {x_0}{(1 - r)^n}\)
Do đó, ta có: \(n = {\log _{(1 - r)}}\frac{{{x_n}}}{{{x_0}}}\)
Gọi giá trị của xe năm thứ n là \({x_n} = 12.000.000\)đ, giá trị xe ban đầu là \({x_0} = 20.000.000\)đ và với hao mòn \(r = 10\% \)
Sau một năm giá trị của xe còn lại là: \({x_1} = {x_0} - r{x_0} = {x_0}(1 - r)\)
Sau hai năm, giá trị của còn lại là: \({x_2} = {x_1} - r{x_1} = {x_1}(1 - r) = {x_0}{(1 - r)^2}\)
Sau n năm, giá trị của xe còn lại là: \({x_n} = {x_{n - 1}} - r{x_{n - 1}} = {x_{n - 1}}(1 - r) = {x_0}{(1 - r)^n}\)
Do đó, ta có: \(n = {\log _{(1 - r)}}\frac{{{x_n}}}{{{x_0}}} = {\log _{(1 - 10\% )}}\frac{{12.000.000}}{{20.000.000}} = 4.848 \approx 5\)năm
Vậy sau 5 năm thì giá trị còn lại của xe là \(12.000.000\)đ
Tìm a để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^3} - 2{x^2} + 3x - 2}}{{x - 1}};\,\,khi\,x \ne 1\\2x + a\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 1\end{array} \right.\)liên tục trên R
Bước 1:Tính \(f({x_0}) = {f_2}({x_0})\)
Bước 2: Tính \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = \mathop {\lim }\limits_{x \to {x_0}} {f_1}(x) = L\)
Bước 3: Nếu \({f_2}({x_0}) = L\) thì hàm số f(x) liên tục tại \({x_0}\)
Nếu \({f_2}({x_0}) \ne L\)thì hàm số f(x) không liên tục tại \({x_0}\).
(Đối với bài toán tìm tham số m để hàm số liên tục tại x0, ta thay bước 3 thành: Giải phương trình L = f2(x0), tìm m)
Ta có hàm số liên tục trên \(( - \infty ;1)\,\,va\,(1; + \infty )\).
Để hs liên tục trên R thì phải liên tục tại \(x = 1 \Rightarrow \mathop {\lim f(x)}\limits_{x \to 1} = f(1)\)
\(\mathop {\lim f(x)}\limits_{x \to 1} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^3} - 2{x^2} + 3x - 2}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} ({x^2} - x + 2) = 2\)
\(f(1) = 2 + a\)
Ta có \(\mathop {\lim f(x)}\limits_{x \to 1} = f(1) \Leftrightarrow \)\(2 + a = 2 \Leftrightarrow a = 0\).
Cho hình chóp \(S.ABC\) có cạnh bên \(SA\) vuông góc với mặt phẳng \((ABC)\) và \(ABC\) là tam giác đều cạnh bằng \(a.\) Biết khoảng cách từ điểm \(A\) đến mặt phẳng \((SBC)\) bàng \(a\sqrt {\frac{6}{{11}}} \) . Tính thể tích khối chóp \(S.ABC\)
Sử dụng phương pháp tính góc giữa hai mặt phẳng
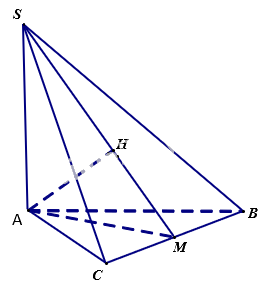
Gọi M là trung điểm của BC thì \(AM \bot BC\)
Dựng AH vuông góc với SM (H thuộc SM)
Vì \(SA \bot \left( {ABC} \right)\) nên \(SA \bot BC\)
Từ (1) và (2) \( \Rightarrow BC \bot \left( {SAM} \right)\)
\( \Rightarrow AH \bot BC\)
Từ (a) và (b) \( \Rightarrow AH \bot \left( {SBC} \right)\)
\( \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AH\)= \(a\sqrt {\frac{6}{{11}}} \)
Xét \(\Delta SAM\) ta có
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{{{\left( {AM} \right)}^2}}} \Leftrightarrow \frac{1}{{{{\left( {a\sqrt {\frac{6}{{11}}} } \right)}^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}\)
\( \Rightarrow SA = \sqrt 2 a\)
Vậy \({V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SA = \frac{1}{3}.\frac{{\sqrt 3 }}{4}{a^2}.\sqrt 2 a = \frac{{\sqrt 6 }}{{12}}{a^3}\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(B.\) Biết \(AD = 2a,\,AB = BC = SA = a.\) Cạnh bên \(SA\) vuông góc với mặt đáy, gọi \(M\) là trung điểm của \(AD.\) Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {SCD} \right)\) theo \(a.\)
Sử dụng phương pháp tính khoảng cách từ điểm đến mặt phẳng
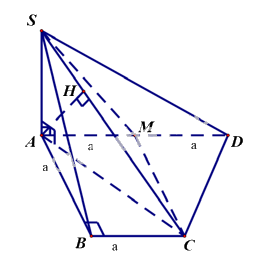
Ta có:
\(\frac{{d\left( {M,\left( {SCD} \right)} \right)}}{{d\left( {A,\left( {SCD} \right)} \right)}} = \frac{{DM}}{{DA}} = \frac{1}{2} \Rightarrow d\left( {M,\left( {SCD} \right)} \right) = \frac{1}{2}d\left( {A,\left( {SCD} \right)} \right).\)
Vì \(M\)là trung điểm của \(AD\) nên có: \(AM = MD = \frac{1}{2}AD = a.\)
Tứ giác \(ABCM\) có: \(BC//AM\,\,\left( {gt} \right)\) và \(BC = AM = a\) nên nó là hình bình hành.
Suy ra: \(CM = AB = a.\)
Tam giác \(ACD\) có \(CM\) là đường trung tuyến và \(CM = AM = MD = \frac{1}{2}AD\) nên tam giác \(ACD\)là tam giác vuông tại \(C.\)
Suy ra: \(CD \bot AC.\)
Ta có:
\(\left\{ \begin{array}{l}CD \bot AC\,\,\left( {cmt} \right)\\CD \bot SA\,\,\,\left( {do\,\,SA \bot \left( {ABCD} \right)} \right)\end{array} \right. \Rightarrow CD \bot \left( {SAC} \right).\)
Ta có:
\(\left\{ \begin{array}{l}CD \bot \left( {SAC} \right)\\CD \subset \left( {SCD} \right)\end{array} \right. \Rightarrow \left( {SCD} \right) \bot \left( {SAC} \right).\)
Trong mặt phẳng \(\left( {SAC} \right),\) kẻ \(AH \bot SC\,\,\left( {H \in SC} \right).\)
Ta có:
\(\left\{ \begin{array}{l}\left( {SCD} \right) \bot \left( {SAC} \right)\\\left( {SCD} \right) \cap \left( {SAC} \right) = SC\\AH \bot SC\\AH \subset \left( {SAC} \right)\end{array} \right. \Rightarrow AH \bot \left( {SCD} \right).\)
Suy ra: \(d\left( {A,\left( {SCD} \right)} \right) = AH.\)
Tam giác \(ABC\) vuông cân tại \(B\) có \(AB = BC = a\) nên \(AC = a\sqrt 2 .\)
Tam giác \(SAC\) vuông tại \(A\,\,\left( {do\,SA \bot \left( {ABCD} \right)} \right)\) có :
\(AH = \frac{{AS.AC}}{{\sqrt {A{S^2} + A{C^2}} }} = \frac{{a.\,a\sqrt 2 }}{{\sqrt {{a^2} + 2{a^2}} }} = \frac{{a\sqrt 6 }}{3}.\)
Suy ra: \(d\left( {A,\left( {SCD} \right)} \right) = AH = \frac{{a\sqrt 6 }}{3}.\)
Suy ra: \(d\left( {M,\left( {SCD} \right)} \right) = \frac{1}{2}.\frac{{a\sqrt 6 }}{3} = \frac{{a\sqrt 6 }}{6}.\)
Vậy \(d\left( {M,\left( {SCD} \right)} \right) = \frac{{a\sqrt 6 }}{6}.\)
Đề thi học kì 2 Toán 11 - Đề số 3: Tổng quan và Hướng dẫn Luyện thi
Học kì 2 Toán 11 là giai đoạn quan trọng, đánh dấu sự chuyển đổi từ kiến thức cơ bản lên các khái niệm nâng cao hơn. Việc chuẩn bị kỹ lưỡng cho kỳ thi học kì là vô cùng cần thiết để đảm bảo kết quả tốt nhất. tusach.vn xin giới thiệu Đề thi học kì 2 Toán 11 - Đề số 3, một công cụ hỗ trợ đắc lực cho quá trình ôn tập của bạn.
Nội dung chính của Đề thi học kì 2 Toán 11 - Đề số 3
Đề thi này bao gồm các chủ đề chính sau:
- Hàm số lượng giác: Các dạng bài tập về xét tính đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất, phương trình lượng giác.
- Phương trình lượng giác: Giải các phương trình lượng giác cơ bản và nâng cao, sử dụng các công thức lượng giác.
- Đạo hàm: Tính đạo hàm của hàm số, ứng dụng đạo hàm để khảo sát hàm số.
- Tích phân: Tính tích phân bất định và tích phân xác định, ứng dụng tích phân để tính diện tích.
- Số phức: Các phép toán trên số phức, phương trình bậc hai với hệ số phức.
Cấu trúc đề thi và dạng bài tập
Đề thi được cấu trúc theo dạng đề thi học kì phổ biến, bao gồm:
- Phần trắc nghiệm: Khoảng 20 câu hỏi, tập trung vào các kiến thức cơ bản và khả năng vận dụng nhanh.
- Phần tự luận: Khoảng 3-5 câu hỏi, yêu cầu trình bày chi tiết lời giải và lập luận logic.
Lợi ích khi luyện tập với Đề thi học kì 2 Toán 11 - Đề số 3
- Làm quen với cấu trúc đề thi: Giúp bạn tự tin hơn khi bước vào phòng thi.
- Rèn luyện kỹ năng giải toán: Cải thiện khả năng áp dụng kiến thức vào giải quyết các bài toán thực tế.
- Kiểm tra kiến thức: Đánh giá mức độ nắm vững kiến thức và xác định các phần cần ôn tập thêm.
- Đáp án chi tiết: Giúp bạn tự đánh giá kết quả và rút kinh nghiệm.
Hướng dẫn luyện thi hiệu quả
Để đạt kết quả tốt nhất, bạn nên:
- Ôn tập lý thuyết: Nắm vững các định nghĩa, định lý và công thức quan trọng.
- Giải nhiều bài tập: Luyện tập thường xuyên với các bài tập khác nhau để làm quen với các dạng bài.
- Sử dụng đề thi thử: Luyện thi với các đề thi thử để làm quen với áp lực thời gian và rèn luyện kỹ năng làm bài.
- Xem lại đáp án và phân tích lỗi sai: Tìm hiểu nguyên nhân gây ra lỗi sai và rút kinh nghiệm để tránh lặp lại.
Tải Đề thi học kì 2 Toán 11 - Đề số 3 ngay hôm nay!
tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức. Hãy tải ngay Đề thi học kì 2 Toán 11 - Đề số 3 và bắt đầu luyện thi ngay hôm nay để đạt kết quả tốt nhất!
Bảng so sánh các đề thi học kì 2 Toán 11 tại tusach.vn
| Đề số | Mức độ khó | Số câu hỏi | Đáp án |
|---|---|---|---|
| Đề số 1 | Dễ | 30 | Có |
| Đề số 2 | Trung bình | 35 | Có |
| Đề số 3 | Khó | 40 | Có |
| Nguồn: tusach.vn | |||