Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1
Tổng quan nội dung
Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1
Tusach.vn xin giới thiệu Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1, được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các câu hỏi trắc nghiệm và tự luận, tập trung vào các chủ đề quan trọng của chương trình học kì 2. Học sinh có thể sử dụng đề thi này để tự đánh giá năng lực và chuẩn bị tốt nhất cho kỳ thi sắp tới.
Đề bài
Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?
- A.
\({\left( {{a^m}} \right)^n} = {a^{m + n}}\)
- B.
\({\left( {{a^m}} \right)^n} = {a^{m - n}}\)
- C.
\({\left( {{a^m}} \right)^n} = {a^{m.n}}\)
- D.
\({\left( {{a^m}} \right)^n} = {a^{\frac{m}{n}}}\)
Chọn đáp án đúng.
Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì:
- A.
\({a^{ - n}} = \frac{1}{{{a^n}}}\)
- B.
\({a^{1 - n}} = \frac{1}{{{a^n}}}\)
- C.
\({a^{\frac{1}{n}}} = \frac{1}{{{a^n}}}\)
- D.
Cả A, B, C đều sai
Chọn đáp án đúng:
- A.\(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[6]{{ab}}\).
- B.\(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[9]{{ab}}\).
- C.\(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{a + b}}\).
- D.\(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).
Rút gọn biểu thức \(P = \frac{{{a^{\sqrt 5 + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}}\) (với \(a > 0\)).
- A.\({a^2}\).
- B.a.
- C.\(\frac{1}{a}\).
- D.\(2{a^2}\).
Với giá trị nào của a thì \({a^{\sqrt 8 }} < \frac{1}{{{a^{ - 3}}}}\)?
- A.
\(a = \frac{3}{4}\)
- B.
\(a = \frac{1}{2}\)
- C.
\(a = 1\)
- D.
\(a = \frac{3}{2}\)
Chọn đáp án đúng.
\({\log _a}b\) xác định khi và chỉ khi:
- A.\(a > 0\).
- B.\(a > 1\).
- C.\(a > 0,a \ne 1,b > 0\).
- D.\(a > 1,b > 0\).
Chọn đáp án đúng.
- A.\({\log _{1000}}{1000^3} = {1000^3}\).
- B.\({\log _{1000}}{1000^3} = \frac{1}{3}\).
- C.\({\log _{1000}}{1000^3} = 3\).
- D.\({\log _{1000}}{1000^3} = {3^{1000}}\).
Khẳng định nào sau đây đúng?
- A.Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\ln a}}\).
- B.Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\log a\).
- C.Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\log a}}\).
- D.Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\ln a\).
Giá trị của phép tính \({4^{{{\log }_{\sqrt 2 }}3}}\) là:
- A.81.
- B.\(9\).
- C.\(\frac{1}{{81}}\).
- D.\(\frac{1}{9}\).
Chọn đáp án đúng:
- A.\({\log _5}15 - 2{\log _5}\sqrt 3 = - 1\).
- B.\({\log _5}15 - 2{\log _5}\sqrt 3 = 1\).
- C.\({\log _5}15 - 2{\log _5}\sqrt 3 = 0\).
- D.\({\log _5}15 - 2{\log _5}\sqrt 3 = \frac{1}{2}\).
Đồ thị hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng:
- A.0.
- B.1.
- C.2.
- D.3.
Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là:
- A.\(D = \left( {0; + \infty } \right)\).
- B.\(D = \left( { - \infty ;0} \right)\).
- C.\(D = \left( { - \infty ; + \infty } \right)\).
- D.Cả A, B, C đều sai.
Hàm số \(y = {\log _2}x\) đồng biến trên khoảng nào sau đây?
- A.\(\left( { - 1; + \infty } \right)\).
- B.\(\left[ {0; + \infty } \right)\).
- C.\(\left[ { - 1; + \infty } \right)\).
- D.\(\left( {1; + \infty } \right)\).
Hàm số nào dưới đây là hàm số mũ?
- A.\(y = {x^{\sqrt 2 }}\).
- B.\(y = {x^{\log 4}}\).
- C.\(y = {\left( {\frac{\pi }{2}} \right)^x}\).
- D.\(y = {\log _2}x\).
Hàm số nào dưới đây có đồ thị như hình dưới?
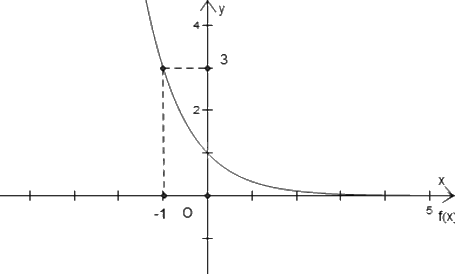
- A.\(y = {3^x}\).
- B.\(y = {\left( {\frac{1}{2}} \right)^x}\).
- C.\(y = {\left( {\frac{1}{3}} \right)^x}\).
- D.\(y = {\left( {\sqrt 2 } \right)^x}\).
Cho hàm số \(f\left( x \right) = {2^x}\). Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - 2;3} \right]\). Khi đó:
- A.\(M.m = 2\).
- B.\(M.m = \frac{1}{2}\)
- C.\(M.m = 4\).
- D.\(M.m = \frac{1}{4}\).
Nghiệm của phương trình \({2^x} = 9\) là:
- A.\(x = {\log _9}2\).
- B.\(x = {\log _2}9\).
- C.\(x = {2^{ - 9}}\)
- D.\(x = \frac{9}{2}\).
Nghiệm của phương trình \({2^{2x - 1}} = {2^x}\) là:
- A.\(x = 0\).
- B.\(x = 2\).
- C.\(x = - 1\).
- D.\(x = 1\).
Phương trình \({\pi ^{x - 3}} = \frac{1}{\pi }\) có nghiệm là:
- A.\(x = 0\).
- B.\(x = 2\).
- C.\(x = - 1\).
- D.\(x = 1\).
Nghiệm của phương trình \({\left( {\frac{1}{{16}}} \right)^{x + 1}} = {64^{2x}}\) là:
- A.\(x = \frac{{ - 1}}{4}\).
- B.\(x = \frac{1}{4}\).
- C.\(x = \frac{{ - 1}}{8}\).
- D.\(x = \frac{1}{8}\).
Tập nghiệm của bất phương trình \({\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge 1\) là:
- A.\(S = \left( {3;\frac{{11}}{3}} \right)\).
- B.\(S = \left( {3;\frac{{11}}{3}} \right]\).
- C.\(S = \left[ {3;\frac{{11}}{3}} \right]\).
- D.\(S = \left[ {3;\frac{{11}}{3}} \right)\).
Phương trình \({\log _3}x + {\log _3}\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right)\) có bao nhiêu nghiệm?
- A.0.
- B.1.
- C.2.
- D.Vô số.
Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt 5 }}} \right)^{2x}} < {25^{1 - x}}\) là:
- A.\(S = \left( { - 2; + \infty } \right)\).
- B.\(S = \left( {2; + \infty } \right)\).
- C.\(S = \left( { - \infty ; - 2} \right)\).
- D.\(S = \left( { - \infty ;2} \right)\).
Góc giữa hai đường thẳng a và b có thể bằng:
- A.1800.
- B.1500.
- C.900.
- D.Cả A, B, C đều sai.
Trong không gian cho hai đường thẳng a và b vuông góc với nhau. Mệnh đề nào dưới đúng?
- A.a và b cắt nhau.
- B.a và b chéo nhau.
- C.a và b cùng nằm trên một mặt phẳng.
- D.Góc giữa a và b bằng \({90^0}\).
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = {100^0}\). Góc giữa hai đường thẳng SA và CD bằng bao nhiêu độ?
- A.\({100^0}\).
- B.\({90^0}\).
- C.\({80^0}\).
- D.\({70^0}\).
Cho hình chóp S. ABCD có đáy ABCD là hình thoi. Gọi M, N lần lượt là trung điểm của các cạnh SB và SD. Khi đó, góc giữa hai đường thẳng AC và MN bằng bao nhiêu độ?
- A.\({100^0}\).
- B.\({90^0}\).
- C.\({80^0}\).
- D.\({70^0}\).
Có bao nhiêu mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước?
- A.Vô số.
- B.1.
- C.2.
- D.3.
Chọn đáp án đúng:
- A.Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
- B.Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
- C.Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
- D.Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
Chọn đáp án đúng.
- A.Có hai đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
- B.Có vô số đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
- C.Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
- D.Có ba đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Cho đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P. Góc giữa hai đường thẳng d và d’ bằng bao nhiêu độ?
- A.\({30^0}\).
- B.\({45^0}\).
- C.\({60^0}\).
- D.\({90^0}\).
Cho hình chóp S. ABCD có ABCD là hình chữ nhật, SA vuông góc với đáy. Đường thẳng BC vuông góc với mặt phẳng nào?
- A.(SAD).
- B.(SCD).
- C.(SAC).
- D.(SAB).
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và H là hình chiếu vuông góc của S lên BC. Chọn khẳng định đúng.
- A.\(BC \bot AB\).
- B.\(BC \bot AH\).
- C.\(BC \bot SC\).
- D.Cả A, B, C đều sai.
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’A và D’B’ bằng:
- A.\({30^0}\).
- B.\({60^0}\).
- C.\({90^0}\).
- D.\({45^0}\).
Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, \(SA \bot \left( {ABCD} \right)\). Chọn đáp án đúng.
- A.\(\left( {AB,SD} \right) = {90^0}\).
- B.\(\left( {AB,SD} \right) = {85^0}\).
- C.\(\left( {AB,SD} \right) = {70^0}\).
- D.\(\left( {AB,SD} \right) = {75^0}\).
Cho hàm số: \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\).
a) Với \(m = \frac{1}{3}\), hãy tìm tập xác định của hàm số trên.
b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định là \(\mathbb{R}\).
Cho hình chóp S. ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC và SD. Chứng minh rằng:
a) \(SC \bot \left( {AHK} \right)\).
b) \(HK \bot \left( {SAC} \right)\) và \(HK \bot AI\).
Có bao nhiêu số tự nhiên x thỏa mãn bất phương trình \({\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{\left( {x - 4} \right)\left( {x + 4} \right)}}{{27}}\)?
Lời giải và đáp án
Cho a là số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là đúng?
- A.
\({\left( {{a^m}} \right)^n} = {a^{m + n}}\)
- B.
\({\left( {{a^m}} \right)^n} = {a^{m - n}}\)
- C.
\({\left( {{a^m}} \right)^n} = {a^{m.n}}\)
- D.
\({\left( {{a^m}} \right)^n} = {a^{\frac{m}{n}}}\)
Đáp án : C
Áp dụng tính chất của phép tính lũy thừa.
Với a là số thực dương và m, n là hai số thực tùy ý thì \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).
Chọn đáp án đúng.
Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì:
- A.
\({a^{ - n}} = \frac{1}{{{a^n}}}\)
- B.
\({a^{1 - n}} = \frac{1}{{{a^n}}}\)
- C.
\({a^{\frac{1}{n}}} = \frac{1}{{{a^n}}}\)
- D.
Cả A, B, C đều sai
Đáp án : A
Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì \({a^{ - n}} = \frac{1}{{{a^n}}}\).
Cho n là một số nguyên dương. Với a là số thực tùy ý khác 0 thì \({a^{ - n}} = \frac{1}{{{a^n}}}\).
Chọn đáp án đúng:
- A.\(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[6]{{ab}}\).
- B.\(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[9]{{ab}}\).
- C.\(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{a + b}}\).
- D.\(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).
Đáp án : D
\(\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}\) (với các biểu thức đều có nghĩa).
Ta có: \(\sqrt[3]{a}.\sqrt[3]{b} = \sqrt[3]{{ab}}\).
Rút gọn biểu thức \(P = \frac{{{a^{\sqrt 5 + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}}\) (với \(a > 0\)).
- A.\({a^2}\).
- B.a.
- C.\(\frac{1}{a}\).
- D.\(2{a^2}\).
Đáp án : B
\({a^m}.{a^n} = {a^{m + n}};{\left( {{a^m}} \right)^n} = {a^{mn}},{a^m}:{a^n} = {a^{m - n}}\) (a khác 0).
\(P = \frac{{{a^{\sqrt 5 + 1}}.{a^{7 - \sqrt 5 }}}}{{{{\left( {{a^{3 + \sqrt 2 }}} \right)}^{3 - \sqrt 2 }}}} \)
\(= \frac{{{a^{\sqrt 5 + 1 + 7 - \sqrt 5 }}}}{{{a^{\left( {3 + \sqrt 2 } \right)\left( {3 - \sqrt 2 } \right)}}}} = \frac{{{a^8}}}{{{a^7}}} = a\).
Với giá trị nào của a thì \({a^{\sqrt 8 }} < \frac{1}{{{a^{ - 3}}}}\)?
- A.
\(a = \frac{3}{4}\)
- B.
\(a = \frac{1}{2}\)
- C.
\(a = 1\)
- D.
\(a = \frac{3}{2}\)
Đáp án : D
Nếu \(a > 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha > \beta \).
Nếu \(0 < a < 1\) thì \({a^\alpha } > {a^\beta } \Leftrightarrow \alpha < \beta \).
Ta có: \(\frac{1}{{{a^{ - 3}}}} = {a^3} = {a^{\sqrt 9 }}\) nên \({a^{\sqrt 8 }} < \frac{1}{{{a^{ - 3}}}} \Leftrightarrow {a^{\sqrt 8 }} < {a^{\sqrt 9 }}\).
Vì \(\sqrt 8 < \sqrt 9 \), mà \({a^{\sqrt 8 }} < {a^{\sqrt 9 }}\) nên \(a > 1\). Do đó, \(a = \frac{3}{2}\) thỏa mãn yêu cầu bài toán.
Chọn đáp án đúng.
\({\log _a}b\) xác định khi và chỉ khi:
- A.\(a > 0\).
- B.\(a > 1\).
- C.\(a > 0,a \ne 1,b > 0\).
- D.\(a > 1,b > 0\).
Đáp án : C
\({\log _a}b\) xác định khi và chỉ khi \(a > 0,a \ne 1,b > 0\).
\({\log _a}b\) xác định khi và chỉ khi \(a > 0,a \ne 1,b > 0\).
Chọn đáp án đúng.
- A.\({\log _{1000}}{1000^3} = {1000^3}\).
- B.\({\log _{1000}}{1000^3} = \frac{1}{3}\).
- C.\({\log _{1000}}{1000^3} = 3\).
- D.\({\log _{1000}}{1000^3} = {3^{1000}}\).
Đáp án : C
Với a, b là số thực dương và \(a \ne 1\) thì \({\log _a}{a^b} = b\).
\({\log _{1000}}{1000^3} = 3\)
Khẳng định nào sau đây đúng?
- A.Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\ln a}}\).
- B.Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\log a\).
- C.Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\frac{1}{{\log a}}\).
- D.Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\ln a\).
Đáp án : B
Lôgarit cơ số 10 của số thực dương b được gọi là lôgarit thập phân của b và kí hiệu logb hay lg b.
Lôgarit cơ số e của số thực dương b được gọi là lôgarit tự nhiên của b và kí hiệu ln b.
Lôgarit cơ số 10 của số thực dương a kí hiệu là \(\log a\).
Giá trị của phép tính \({4^{{{\log }_{\sqrt 2 }}3}}\) là:
- A.81.
- B.\(9\).
- C.\(\frac{1}{{81}}\).
- D.\(\frac{1}{9}\).
Đáp án : A
Với a, b là số thực dương và \(a \ne 1\) thì \({a^{{{\log }_a}b}} = b,{\log _{{a^\alpha }}}b = \frac{1}{\alpha }{\log _a}b;{\log _a}{b^\alpha } = \alpha {\log _a}b\).
\({4^{{{\log }_{\sqrt 2 }}3}} = {2^{2{{\log }_{{2^{\frac{1}{2}}}}}3}} = {2^{4{{\log }_2}3}} = {2^{{{\log }_2}{3^4}}} = 81\)
Chọn đáp án đúng:
- A.\({\log _5}15 - 2{\log _5}\sqrt 3 = - 1\).
- B.\({\log _5}15 - 2{\log _5}\sqrt 3 = 1\).
- C.\({\log _5}15 - 2{\log _5}\sqrt 3 = 0\).
- D.\({\log _5}15 - 2{\log _5}\sqrt 3 = \frac{1}{2}\).
Đáp án : B
Với a, b là số thực dương và \(a \ne 1\) thì \({\log _a}{b^\alpha } = \alpha {\log _a}b,\log {\,_a}a = 1\)
Với a là số thực dương, \(a \ne 1\), \(M > 0,N > 0\) thì \({\log _a}\frac{M}{N} = {\log _a}M - {\log _a}N\).
\({\log _5}15 - 2{\log _5}\sqrt 3 = {\log _5}15 - {\log _5}3 = {\log _5}\frac{{15}}{3} = {\log _5}5 = 1\)
Đồ thị hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng:
- A.0.
- B.1.
- C.2.
- D.3.
Đáp án : B
Đồ thị hàm số hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng 1.
Đồ thị hàm số hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) cắt trục tung tại điểm có tung độ bằng 1.
Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là:
- A.\(D = \left( {0; + \infty } \right)\).
- B.\(D = \left( { - \infty ;0} \right)\).
- C.\(D = \left( { - \infty ; + \infty } \right)\).
- D.Cả A, B, C đều sai.
Đáp án : C
Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là \(D = \left( { - \infty ; + \infty } \right)\).
Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) có tập xác định là \(D = \left( { - \infty ; + \infty } \right)\).
Hàm số \(y = {\log _2}x\) đồng biến trên khoảng nào sau đây?
- A.\(\left( { - 1; + \infty } \right)\).
- B.\(\left[ {0; + \infty } \right)\).
- C.\(\left[ { - 1; + \infty } \right)\).
- D.\(\left( {1; + \infty } \right)\).
Đáp án : D
Nếu \(a > 1\) thì hàm số \(y = {\log _2}x\) đồng biến trên \(\left( {0; + \infty } \right)\).
Vì \(2 > 1\) nên hàm số \(y = {\log _2}x\) đồng biến trên \(\left( {0; + \infty } \right)\). Do đó, hàm số \(y = {\log _2}x\) đồng biến trên \(\left( {1; + \infty } \right)\)
Hàm số nào dưới đây là hàm số mũ?
- A.\(y = {x^{\sqrt 2 }}\).
- B.\(y = {x^{\log 4}}\).
- C.\(y = {\left( {\frac{\pi }{2}} \right)^x}\).
- D.\(y = {\log _2}x\).
Đáp án : C
Hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\) được gọi là hàm số mũ cơ số a.
Hàm số \(y = {\left( {\frac{\pi }{2}} \right)^x}\) được gọi là hàm số mũ.
Hàm số nào dưới đây có đồ thị như hình dưới?
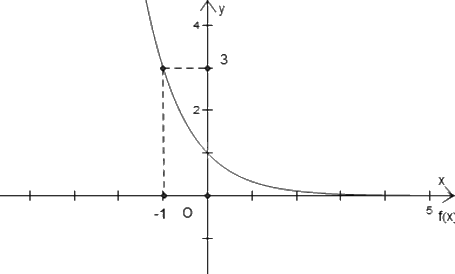
- A.\(y = {3^x}\).
- B.\(y = {\left( {\frac{1}{2}} \right)^x}\).
- C.\(y = {\left( {\frac{1}{3}} \right)^x}\).
- D.\(y = {\left( {\sqrt 2 } \right)^x}\).
Đáp án : C
Xét xem đồ thị hàm số nào đi qua điểm \(\left( { - 1;3} \right)\) và (0;1) thì đó là đồ thị hàm số cần tìm.
Ta thấy đồ thị hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) đi qua điểm \(\left( { - 1;3} \right)\) và (0;1) nên hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) là hàm số cần tìm.
Cho hàm số \(f\left( x \right) = {2^x}\). Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của f(x) trên đoạn \(\left[ { - 2;3} \right]\). Khi đó:
- A.\(M.m = 2\).
- B.\(M.m = \frac{1}{2}\)
- C.\(M.m = 4\).
- D.\(M.m = \frac{1}{4}\).
Đáp án : A
Cho hàm số \(y = {a^x}\left( {a > 0,a \ne 1} \right)\):
+ Nếu \(a > 1\) thì hàm số đồng biến trên \(\mathbb{R}\).
+ Nếu \(0 < a < 1\) thì hàm số nghịch biến trên \(\mathbb{R}\).
Vì \(2 > 1\) nên hàm số \(f\left( x \right) = {2^x}\) đồng biến trên \(\mathbb{R}\).
Do đó, \(\mathop {\max }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( 3 \right) = {2^3} = 8;\mathop {\min }\limits_{\left[ { - 2;3} \right]} f\left( x \right) = f\left( { - 2} \right) = {2^{ - 2}} = \frac{1}{4}\)
Suy ra: \(M = 8,m = \frac{1}{4} \Rightarrow Mm = 8.\frac{1}{4} = 2\).
Nghiệm của phương trình \({2^x} = 9\) là:
- A.\(x = {\log _9}2\).
- B.\(x = {\log _2}9\).
- C.\(x = {2^{ - 9}}\)
- D.\(x = \frac{9}{2}\).
Đáp án : B
Cho phương trình \({a^x} = b\left( {a > 0,a \ne 1} \right)\):
+ Nếu \(b \le 0\) thì phương trình vô nghiệm.
+ Nếu \(b > 0\) thì phương trình có nghiệm duy nhất \(x = {\log _a}b\).
\({2^x} = 9 \Leftrightarrow x = {\log _2}9\)
Vậy phương trình có nghiệm là \(x = {\log _2}9\).
Nghiệm của phương trình \({2^{2x - 1}} = {2^x}\) là:
- A.\(x = 0\).
- B.\(x = 2\).
- C.\(x = - 1\).
- D.\(x = 1\).
Đáp án : D
\({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)
\({2^{2x - 1}} = {2^x} \Leftrightarrow 2x - 1 = x \Leftrightarrow x = 1\)
Vậy phương trình đã cho có nghiệm \(x = 1\)
Phương trình \({\pi ^{x - 3}} = \frac{1}{\pi }\) có nghiệm là:
- A.\(x = 0\).
- B.\(x = 2\).
- C.\(x = - 1\).
- D.\(x = 1\).
Đáp án : B
\({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)
\({\pi ^{x - 3}} = \frac{1}{\pi } \Leftrightarrow {\pi ^{x - 3}} = {\pi ^{ - 1}} \Leftrightarrow x - 3 = - 1 \Leftrightarrow x = 2\)
Vậy phương trình có nghiệm \(x = 2\).
Nghiệm của phương trình \({\left( {\frac{1}{{16}}} \right)^{x + 1}} = {64^{2x}}\) là:
- A.\(x = \frac{{ - 1}}{4}\).
- B.\(x = \frac{1}{4}\).
- C.\(x = \frac{{ - 1}}{8}\).
- D.\(x = \frac{1}{8}\).
Đáp án : A
\({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)
\({\left( {\frac{1}{{16}}} \right)^{x + 1}} = {64^{2x}} \Leftrightarrow {4^{ - 2\left( {x + 1} \right)}} = {4^{3.2x}} \Leftrightarrow - 2x - 2 = 6x \Leftrightarrow 8x = - 2 \Leftrightarrow x = \frac{{ - 1}}{4}\)
Tập nghiệm của bất phương trình \({\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge 1\) là:
- A.\(S = \left( {3;\frac{{11}}{3}} \right)\).
- B.\(S = \left( {3;\frac{{11}}{3}} \right]\).
- C.\(S = \left[ {3;\frac{{11}}{3}} \right]\).
- D.\(S = \left[ {3;\frac{{11}}{3}} \right)\).
Đáp án : B
Nếu \(0 < a < 1\) thì \({\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) \le v\left( x \right)\end{array} \right.\).
\({\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge 1 \Leftrightarrow {\log _{\frac{2}{3}}}\left( {x - 3} \right) \ge {\log _{\frac{2}{3}}}\frac{2}{3} \Leftrightarrow \left\{ \begin{array}{l}x - 3 > 0\\x - 3 \le \frac{2}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 3\\x \le \frac{{11}}{3}\end{array} \right.\)
Do đó, tập nghiệm của bất phương trình là: \(S = \left( {3;\frac{{11}}{3}} \right]\).
Phương trình \({\log _3}x + {\log _3}\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right)\) có bao nhiêu nghiệm?
- A.0.
- B.1.
- C.2.
- D.Vô số.
Đáp án : B
Với \(a > 0,a \ne 1\) thì \({\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.\) (có thể thay \(u\left( x \right) > 0\) bằng \(v\left( x \right) > 0\))
Điều kiện: \(x > 0\)
\({\log _3}x + {\log _3}\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right) \Leftrightarrow {\log _3}x\left( {x + 1} \right) = {\log _3}\left( {5x + 12} \right)\)
\( \Leftrightarrow {x^2} + x = 5x + 12 \Leftrightarrow {x^2} - 4x - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\left( L \right)\\x = 6\left( {TM} \right)\end{array} \right.\)
Vậy phương trình đã cho có một nghiệm là \(x = 6\)
Tập nghiệm của bất phương trình \({\left( {\frac{1}{{\sqrt 5 }}} \right)^{2x}} < {25^{1 - x}}\) là:
- A.\(S = \left( { - 2; + \infty } \right)\).
- B.\(S = \left( {2; + \infty } \right)\).
- C.\(S = \left( { - \infty ; - 2} \right)\).
- D.\(S = \left( { - \infty ;2} \right)\).
Đáp án : D
Với \(a > 1\) thì \({a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) > v\left( x \right)\)
\({\left( {\frac{1}{{\sqrt 5 }}} \right)^{2x}} < {25^{1 - x}} \Leftrightarrow {5^{\frac{{ - 2x}}{2}}} < {5^{2\left( {1 - x} \right)}} \Leftrightarrow - x < 2 - 2x\left( {do\;5 > 1} \right) \Leftrightarrow x < 2\)
Vậy tập nghiệm của bất phương trình đã cho là: \(S = \left( { - \infty ;2} \right)\).
Góc giữa hai đường thẳng a và b có thể bằng:
- A.1800.
- B.1500.
- C.900.
- D.Cả A, B, C đều sai.
Đáp án : C
Góc giữa hai đường thẳng có số đo không vượt quá 900.
Vì góc giữa hai đường thẳng có số đo không vượt quá 900 nên góc giữa hai đường thẳng có thể bằng 900.
Trong không gian cho hai đường thẳng a và b vuông góc với nhau. Mệnh đề nào dưới đúng?
- A.a và b cắt nhau.
- B.a và b chéo nhau.
- C.a và b cùng nằm trên một mặt phẳng.
- D.Góc giữa a và b bằng \({90^0}\).
Đáp án : D
Hai đường thẳng vuông góc với nhau nếu góc giữa chúng bằng \({90^0}\).
Trong không gian cho hai đường thẳng a và b vuông góc với nhau thì góc giữa chúng bằng \({90^0}\).
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành và \(\widehat {SAB} = {100^0}\). Góc giữa hai đường thẳng SA và CD bằng bao nhiêu độ?
- A.\({100^0}\).
- B.\({90^0}\).
- C.\({80^0}\).
- D.\({70^0}\).
Đáp án : C
+ Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu \(\left( {a,b} \right)\) hoặc \(\widehat {\left( {a;b} \right)}\).
+ Góc giữa hai đường thẳng không vượt quá \({90^0}\).
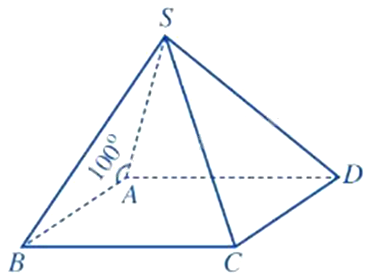
Vì ABCD là hình bình hành nên \(AB//CD\)
Do đó, \(\left( {SA,CD} \right) = \left( {SA,AB} \right) = {180^0} - \widehat {SAB} = {80^0}\)
Cho hình chóp S. ABCD có đáy ABCD là hình thoi. Gọi M, N lần lượt là trung điểm của các cạnh SB và SD. Khi đó, góc giữa hai đường thẳng AC và MN bằng bao nhiêu độ?
- A.\({100^0}\).
- B.\({90^0}\).
- C.\({80^0}\).
- D.\({70^0}\).
Đáp án : B
Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
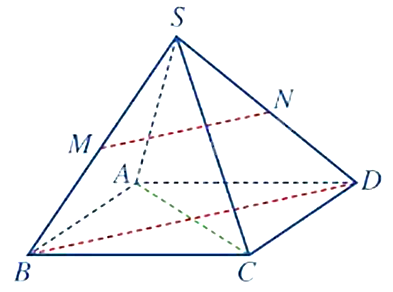
Vì M, N lần lượt là trung điểm của các cạnh SB và SD nên MN là đường trung bình của tam giác SBD, do đó, MN//BD.
Vì ABCD là hình thoi nên \(AC \bot BD\)
Vì \(AC \bot BD\), MN//BD nên \(AC \bot MN \Rightarrow \left( {AC,MN} \right) = {90^0}\).
Có bao nhiêu mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước?
- A.Vô số.
- B.1.
- C.2.
- D.3.
Đáp án : B
Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Chọn đáp án đúng:
- A.Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
- B.Hai đường thẳng cùng vuông góc với một mặt phẳng thì song song với nhau.
- C.Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.
- D.Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì cắt nhau.
Đáp án : A
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Chọn đáp án đúng.
- A.Có hai đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
- B.Có vô số đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
- C.Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
- D.Có ba đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Đáp án : C
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Có duy nhất một đường thẳng cùng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
Cho đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P. Góc giữa hai đường thẳng d và d’ bằng bao nhiêu độ?
- A.\({30^0}\).
- B.\({45^0}\).
- C.\({60^0}\).
- D.\({90^0}\).
Đáp án : D
Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Vì đường thẳng d vuông góc với mặt phẳng (P) và đường thẳng d’ nằm trong mặt phẳng P nên \(d \bot d' \Rightarrow \left( {d,d'} \right) = {90^0}\)
Cho hình chóp S. ABCD có ABCD là hình chữ nhật, SA vuông góc với đáy. Đường thẳng BC vuông góc với mặt phẳng nào?
- A.(SAD).
- B.(SCD).
- C.(SAC).
- D.(SAB).
Đáp án : D
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
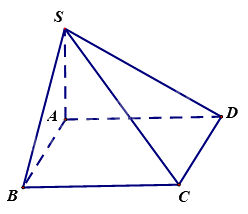
Vì \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\)
Mà ABCD là hình chữ nhật nên \(BC \bot AB\)
Ta có: \(SA \bot BC,BC \bot AB,\) AB và SA cắt nhau tại A và nằm trong mặt phẳng (SAB).
Do đó, \(BC \bot \left( {SAB} \right)\)
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và H là hình chiếu vuông góc của S lên BC. Chọn khẳng định đúng.
- A.\(BC \bot AB\).
- B.\(BC \bot AH\).
- C.\(BC \bot SC\).
- D.Cả A, B, C đều sai.
Đáp án : B
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
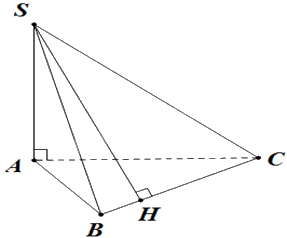
Vì \(SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC\), mà \(BC \bot SH\) và SA và SH cắt nhau tại S và nằm trong mặt phẳng (SAH) nên \(BC \bot \left( {SAH} \right)\).
Lại có: \(AH \subset \left( {SAH} \right)\) nên \(BC \bot AH\).
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng A’A và D’B’ bằng:
- A.\({30^0}\).
- B.\({60^0}\).
- C.\({90^0}\).
- D.\({45^0}\).
Đáp án : C
Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
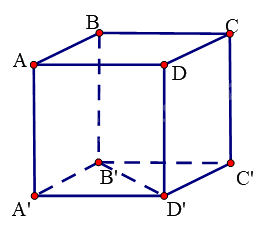
Vì ABCD.A’B’C’D’ là hình lập phương nên \(AA' \bot \left( {A'B'C'D'} \right)\), mà \(B'D' \subset \left( {A'B'C'D'} \right)\) nên \(AA' \bot B'D'\). Do đó, góc giữa hai đường thẳng A’A và D’B’ bằng \({90^0}\).
Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A và D, \(SA \bot \left( {ABCD} \right)\). Chọn đáp án đúng.
- A.\(\left( {AB,SD} \right) = {90^0}\).
- B.\(\left( {AB,SD} \right) = {85^0}\).
- C.\(\left( {AB,SD} \right) = {70^0}\).
- D.\(\left( {AB,SD} \right) = {75^0}\).
Đáp án : A
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
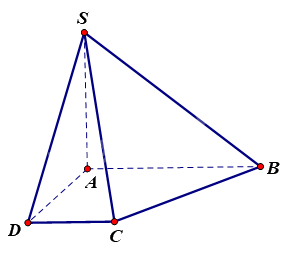
Vì \(SA \bot \left( {ABCD} \right),AB \subset \left( {ABCD} \right) \Rightarrow SA \bot AB\).
Vì ABCD là hình thang vuông tại A nên \(AB \bot AD\).
Ta có: \(AB \bot AD\), \(SA \bot AB\) và SA và AD cắt nhau tại A và nằm trong mặt phẳng (SAD)
Do đó, \(AB \bot \left( {SAD} \right) \Rightarrow AB \bot SD\). Suy ra, \(\left( {AB,SD} \right) = {90^0}\).
Cho hàm số: \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\).
a) Với \(m = \frac{1}{3}\), hãy tìm tập xác định của hàm số trên.
b) Tìm tất cả các giá trị của tham số m để hàm số trên có tập xác định là \(\mathbb{R}\).
+ Hàm số có dạng \(y = \frac{1}{{\sqrt {u\left( x \right)} }}\) xác định khi \(u\left( x \right) > 0\).
+ Hàm \(y = {\log _a}u\left( x \right)\left( {a > 0,a \ne 1} \right)\) xác định khi \(u\left( x \right) > 0\).
a) Với \(m = \frac{1}{3}\) ta có: \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 1} \right)} }}\).
Hàm số \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 1} \right)} }}\) xác định khi \({\log _3}\left( {{x^2} - 2x + 1} \right) > 0 \Leftrightarrow {x^2} - 2x + 1 > 1 \Leftrightarrow {x^2} - 2x > 0 \Leftrightarrow \left[ \begin{array}{l}x > 2\\x < 0\end{array} \right.\)
Vậy với \(m = \frac{1}{3}\) thì tập xác định của hàm số là: \(D = \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\).
b) Hàm số \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\) có tập xác định là \(\mathbb{R}\) khi và chỉ khi \({\log _3}\left( {{x^2} - 2x + 3m} \right) > 0\) với mọi \(x \in \mathbb{R}\)
\( \Leftrightarrow {x^2} - 2x + 3m > 1\) với mọi \(x \in \mathbb{R}\)
\( \Leftrightarrow {x^2} - 2x + 3m - 1 > 0\) với mọi \(x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\\Delta ' < 0\end{array} \right. \Leftrightarrow {\left( { - 1} \right)^2} - 3m + 1 < 0 \Leftrightarrow m > \frac{2}{3}\)
Vậy với \(m > \frac{2}{3}\) thì hàm số \(y = \frac{1}{{\sqrt {{{\log }_3}\left( {{x^2} - 2x + 3m} \right)} }}\) có tập xác định là \(\mathbb{R}\).
Cho hình chóp S. ABCD có đáy ABCD là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC và SD. Chứng minh rằng:
a) \(SC \bot \left( {AHK} \right)\).
b) \(HK \bot \left( {SAC} \right)\) và \(HK \bot AI\).
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
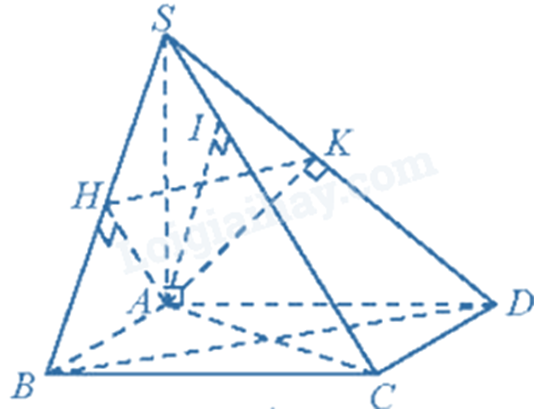
a) Vì \(SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \Rightarrow SA \bot DC\)
Vì ABCD là hình vuông nên \(DC \bot AD\).
Mà SA và AD cắt nhau tại A và nằm trong mặt phẳng (SAD). Do đó, \(DC \bot \left( {SAD} \right)\)
Lại có: \(AK \subset \left( {SAD} \right) \Rightarrow DC \bot AK\). Mặt khác, \(AK \bot SD \Rightarrow AK \bot \left( {SDC} \right) \Rightarrow AK \bot SC\)
Vì \(SA \bot \left( {ABCD} \right),BC \subset \left( {ABCD} \right) \Rightarrow SA \bot BC\)
Vì ABCD là hình vuông nên \(BC \bot AB\).
Mà SA và AB cắt nhau tại A và nằm trong mặt phẳng (SAB). Do đó, \(BC \bot \left( {SAB} \right)\)
Lại có: \(AH \subset \left( {SAB} \right) \Rightarrow BC \bot AH\). Mặt khác, \(AH \bot SB \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\)
Ta có: \(AK \bot SC\), \(AH \bot SC\) và AK và AH cắt nhau tại A nằm trong mặt phẳng (AHK) nên \(SC \bot \left( {AHK} \right)\).
b) Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow \left\{ \begin{array}{l}SA \bot AB\\SA \bot AD\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\widehat {SAB} = {90^0}\\\widehat {SAD} = {90^0}\end{array} \right.\)
Tam giác SAB và tam giác SAD có: SA là cạnh chung, \(\widehat {SAB} = \widehat {SAD} = {90^0}\), \(AB = AD\).
Do đó, \(\Delta SAB = \Delta SAD\left( {c.g.c} \right) \Rightarrow SB = SD\), \(SH = SK\).
Suy ra: \(\frac{{SH}}{{SB}} = \frac{{SK}}{{SD}}\). Do đó, HK//BD (1)
Vì ABCD là hình vuông nên \(AC \bot BD\).
Vì \(SA \bot \left( {ABCD} \right),DB \subset \left( {ABCD} \right) \Rightarrow SA \bot DB\)
Mà SA và AC cắt nhau tại A và nằm trong mặt phẳng (SAC) nên \(DB \bot \left( {SAC} \right)\) (2)
Từ (1) và (2) ta có: \(HK \bot \left( {SAC} \right)\). Mà \(AI \subset \left( {SAC} \right)\), suy ra \(HK \bot AI\).
Có bao nhiêu số tự nhiên x thỏa mãn bất phương trình \({\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{\left( {x - 4} \right)\left( {x + 4} \right)}}{{27}}\)?
Nếu \(a > 1\) thì \({\log _a}u\left( x \right) < {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) < v\left( x \right)\end{array} \right.\).
TXĐ: \(D = \left( { - \infty ; - 4} \right) \cup \left( {4; + \infty } \right)\).
Ta có: \({\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{\left( {x - 4} \right)\left( {x + 4} \right)}}{{27}}\)
\(\begin{array}{l} \Leftrightarrow {\rm{lo}}{{\rm{g}}_3}\frac{{{x^2} - 16}}{{343}} < {\rm{lo}}{{\rm{g}}_7}\frac{{{x^2} - 16}}{{27}}\\ \Leftrightarrow {\rm{lo}}{{\rm{g}}_3}7.\left[ {{\rm{lo}}{{\rm{g}}_7}\left( {{x^2} - 16} \right) - 3} \right] < {\rm{lo}}{{\rm{g}}_7}\left( {{x^2} - 16} \right) - 3{\rm{lo}}{{\rm{g}}_7}3\\ \Leftrightarrow \left( {{\rm{lo}}{{\rm{g}}_3}7 - 1} \right){\rm{.lo}}{{\rm{g}}_7}\left( {{x^2} - 16} \right) < 3{\rm{lo}}{{\rm{g}}_3}7 - 3{\rm{lo}}{{\rm{g}}_7}3\\ \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < \frac{{3\left( {{{\log }_3}7 - {{\log }_7}3} \right)}}{{{{\log }_3}7 - 1}}\end{array}\)
\( \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < \frac{{3\left( {{{\log }_3}7 - \frac{1}{{{{\log }_3}7}}} \right)}}{{{{\log }_3}7 - 1}}\)\( \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < \frac{{3\left( {{{\log }_3}7 + 1} \right)}}{{{{\log }_3}7}}\)
\(\begin{array}{l} \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < 3\left( {1 + {{\log }_7}3} \right)\\ \Leftrightarrow {\log _7}\left( {{x^2} - 16} \right) < {\log _7}{21^3}\end{array}\)
\( \Leftrightarrow {x^2} - 16 < {21^3} \Leftrightarrow - \sqrt {9277} < x < \sqrt {9277} \)
Kết hợp với điều kiện xác định ta có: \(\left[ \begin{array}{l} - \sqrt {9277} < x < - 4\\4 < x < \sqrt {9277} \end{array} \right.\)
Vì x là số tự nhiên nên \(x \in \left\{ {5;6;7;...;96} \right\}\).
Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1: Tổng quan và Hướng dẫn
Kỳ thi giữa học kỳ 2 Toán 11 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh. Đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1 do tusach.vn cung cấp là một công cụ hữu ích giúp học sinh ôn luyện và làm quen với cấu trúc đề thi thực tế.
Cấu trúc đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1
Đề thi thường bao gồm hai phần chính:
- Phần trắc nghiệm: Kiểm tra kiến thức cơ bản và khả năng vận dụng nhanh các công thức, định lý.
- Phần tự luận: Đòi hỏi học sinh trình bày chi tiết lời giải, áp dụng kiến thức vào giải quyết các bài toán phức tạp.
Các chủ đề chính thường xuất hiện trong đề thi
- Đại số: Phương trình, bất phương trình, hệ phương trình, hàm số bậc hai.
- Hình học: Vectơ, tích vô hướng, đường thẳng, đường tròn, elip, hypebol, parabol.
- Phân tích tổ hợp và xác suất: Hoán vị, tổ hợp, chỉnh hợp, xác suất.
Lợi ích khi luyện tập với đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1
- Nắm vững kiến thức: Giúp học sinh củng cố kiến thức đã học và phát hiện những lỗ hổng kiến thức cần bổ sung.
- Rèn luyện kỹ năng: Phát triển kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
- Làm quen với cấu trúc đề thi: Giúp học sinh tự tin hơn khi bước vào phòng thi.
- Đánh giá năng lực: Cho phép học sinh tự đánh giá năng lực và có kế hoạch ôn tập phù hợp.
Hướng dẫn giải đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1
Để đạt kết quả tốt nhất, học sinh nên:
- Đọc kỹ đề bài và xác định yêu cầu của từng câu hỏi.
- Sử dụng các công thức, định lý đã học để giải quyết bài toán.
- Trình bày lời giải rõ ràng, mạch lạc và dễ hiểu.
- Kiểm tra lại kết quả trước khi nộp bài.
Tải đề thi và đáp án
Tusach.vn cung cấp đề thi giữa kì 2 Toán 11 Kết nối tri thức - Đề số 1 cùng với đáp án chi tiết. Học sinh có thể tải đề thi miễn phí về máy tính hoặc điện thoại để luyện tập. Ngoài ra, chúng tôi còn cung cấp nhiều đề thi khác với các mức độ khó khác nhau để đáp ứng nhu cầu ôn tập của mọi học sinh.
Lời khuyên
Hãy dành thời gian ôn tập kỹ lưỡng và luyện tập thường xuyên với các đề thi khác nhau. Chúc các em học sinh đạt kết quả cao trong kỳ thi giữa học kỳ 2!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Phương trình | Cao |
| Vectơ | Trung bình |
| Hàm số bậc hai | Cao |
| Nguồn: tusach.vn | |