Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8
Tổng quan nội dung
Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8
Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8 là một trong những đề thi quan trọng giúp học sinh đánh giá năng lực và kiến thức đã học trong giai đoạn đầu năm học. Đề thi này được biên soạn bám sát chương trình sách giáo khoa Kết nối tri thức, đảm bảo tính chính xác và phù hợp với trình độ của học sinh.
tusach.vn cung cấp đề thi này kèm theo đáp án chi tiết, giúp học sinh tự ôn luyện và kiểm tra kiến thức một cách hiệu quả.
Đề bài
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
- A.
\({30^o}\)
- B.
\({45^o}\)
- C.
\({60^o}\)
- D.
\({90^o}\)
Cho \(\cos \alpha = - \frac{1}{4}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\sin \alpha \) là?
- A.
\(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
- B.
\(\sin \alpha = - \frac{{\sqrt {15} }}{4}\)
- C.
\(\sin \alpha = \frac{{15}}{{16}}\)
- D.
\(\sin \alpha = - \frac{{15}}{{16}}\)
Giá trị lượng giác \(\cos \left( {\frac{{37\pi }}{{12}}} \right)\) bằng?
- A.
\(\frac{{\sqrt 6 + \sqrt 2 }}{4}\)
- B.
\(\frac{{\sqrt 6 - \sqrt 2 }}{4}\)
- C.
\( - \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
- D.
\( - \frac{{\sqrt 6 - \sqrt 2 }}{4}\)
Hàm số nào sau đây là hàm số chẵn?
- A.
\(y = \left| {\sin x} \right|\)
- B.
\(y = {x^2}.\sin x\)
- C.
\(y = \frac{x}{{\cos x}}\)
- D.
\(y = x + \sin x\)
Nghiệm của phương trình \(\cos x = 0\) là?
- A.
\(x = k2\pi ,k \in \mathbb{Z}\)
- B.
\(x = k\pi ,k \in \mathbb{Z}\)
- C.
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
- D.
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\)
Số hạng thứ 3 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = 2{u_{n - 1}} + 3}\end{array}} \right.\) là?
- A.
5
- B.
8
- C.
28
- D.
13
Dãy số nào sau đây là cấp số cộng?
- A.
1; 4; 8; 10
- B.
2; 3; 5; 8; 9
- C.
0; 2; 4; 6; 8
- D.
1; 3; -5; -7; -9
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 12\) và công bội \(q = - 2\). Số hạng thứ sáu của cấp số nhân đã cho bằng
- A.
2
- B.
-384
- C.
-24
- D.
-34
Số lượng khách hàng nữ mua bảo hiểm nhân thọ trong một ngày được thống kê trong bảng tần số ghép nhóm sau:

Giá trị đại diện của nhóm [30;40) là
- A.
40
- B.
30
- C.
35
- D.
9
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng).

Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng sau đây?
- A.
[7;9)
- B.
[9;11)
- C.
[11;13)
- D.
[13;15)
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \([0;2\pi ]\) là
- A.
3
- B.
1
- C.
2
- D.
4
Cho cấp số cộng \(({u_n})\) có \({u_5} = - 10\) và \({u_{15}} = 60\). Tổng 20 số hạng đầu tiên của cấp số cộng là
- A.
560
- B.
480
- C.
570
- D.
475
Cho phương trình lượng giác \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\). Khi đó
a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Cho \(\cos \alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó
a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
c) \(\tan \alpha = \sqrt {15} \)
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n} + 1\). Khi đó
a) Dãy số \(({u_n})\) là dãy số tăng
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_6} = 65\)
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng A, B được cho ở bảng sau:

a) Giá trị đại diện của nhóm [150;155) bằng 152,5
b) Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [155;160)
c) Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [160;165)
d) Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A
Hằng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu h (m) của mực nước theo thời gian t (giờ) trong một ngày được cho bởi công thức \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) với \(0 \le t \le 24\). Tính thời điểm mực nước tại cảng cao nhất.
Đáp án:
Phương trình \(2\sin 2x + 4\cos x = 0\) có bao nhiêu nghiệm trong khoảng (0;3000)?
Đáp án:
Công ty cây xanh X trồng 496 cây hoa trong một khu vườn hình tam giác như sau: hàng thứ nhất trồng 1 cây hoa, kể từ hàng thứ hai trở đi số cây hoa trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi công ty cây xanh X trồng được bao nhiêu hàng cây trong khu vườn hình tam giác đó.
Đáp án:
Cho dãy số \(({u_n})\) biết \({u_n} = n + \frac{1}{n}\). Tìm m để dãy số \(({u_n})\) bị chặn dưới bởi m.
Đáp án:
Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A.

Số học sinh có chiều cao bao nhiêu cm là nhiều nhất (làm tròn đến hàng đơn vị)?
Đáp án:
Trong một hội thao, thời gian chạy 200 m của một nhóm vận động viên được ghi lại trong bảng sau:

Dựa vào bảng dữ liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy không quá bao nhiêu giây (kết quả làm tròn đến hàng phần mười)?
Đáp án:
Lời giải và đáp án
Góc có số đo \(\frac{\pi }{6}\) radian bằng bao nhiêu độ?
- A.
\({30^o}\)
- B.
\({45^o}\)
- C.
\({60^o}\)
- D.
\({90^o}\)
Đáp án : A
Áp dụng quan hệ giữa radian và độ: \(1rad = {\left( {\frac{{180}}{\pi }} \right)^o}\), \({1^o} = \frac{\pi }{{180}}rad\).
Ta có: \(\frac{\pi }{6}rad = \frac{\pi }{6}.\frac{{{{180}^o}}}{\pi } = {30^o}\).
Cho \(\cos \alpha = - \frac{1}{4}\) với \(\pi < \alpha < \frac{{3\pi }}{2}\). Giá trị của \(\sin \alpha \) là?
- A.
\(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
- B.
\(\sin \alpha = - \frac{{\sqrt {15} }}{4}\)
- C.
\(\sin \alpha = \frac{{15}}{{16}}\)
- D.
\(\sin \alpha = - \frac{{15}}{{16}}\)
Đáp án : B
Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và sử dụng đường tròn lượng giác để xét dấu.
Ta có: \({\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - {\left( {\frac{1}{4}} \right)^2} = \frac{{15}}{{16}}\), suy ra \(\sin \alpha = \pm \frac{{\sqrt {15} }}{4}\).
Vì \(\pi < \alpha < \frac{{3\pi }}{2}\) nên điểm cuối của cung \(\alpha \) thuộc cung phần tư thứ III, do đó \(\sin \alpha < 0\).
Vậy \(\sin \alpha = - \frac{{\sqrt {15} }}{4}\).
Giá trị lượng giác \(\cos \left( {\frac{{37\pi }}{{12}}} \right)\) bằng?
- A.
\(\frac{{\sqrt 6 + \sqrt 2 }}{4}\)
- B.
\(\frac{{\sqrt 6 - \sqrt 2 }}{4}\)
- C.
\( - \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
- D.
\( - \frac{{\sqrt 6 - \sqrt 2 }}{4}\)
Đáp án : C
Sử dụng công thức cộng lượng giác \(\cos (a - b) = \cos a.\cos b + \sin b.\sin a\).
\(\cos \frac{{37\pi }}{{12}} = \cos \left( {3\pi + \frac{\pi }{{12}}} \right) = \cos \left( {\pi + \frac{\pi }{{12}}} \right) = - \cos \frac{\pi }{{12}} = - \cos \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right)\)
\( = - \left( {\cos \frac{\pi }{3}.\cos \frac{\pi }{4} + \sin \frac{\pi }{3}.\sin \frac{\pi }{4}} \right) = - \frac{{\sqrt 6 + \sqrt 2 }}{4}\).
Hàm số nào sau đây là hàm số chẵn?
- A.
\(y = \left| {\sin x} \right|\)
- B.
\(y = {x^2}.\sin x\)
- C.
\(y = \frac{x}{{\cos x}}\)
- D.
\(y = x + \sin x\)
Đáp án : A
Cho hàm số y = f(x) liên tục và xác định trên khoảng (đoạn) K. Với mỗi \(x \in K\) thì \( - x \in K\).
- Nếu f(x) = f(-x) thì hàm số y = f(x) là hàm số chẵn trên tập xác định.
- Nếu f(-x) = -f(x) thì hàm số y = f(x) là hàm số lẻ trên tập xác định.
Xét phương án A, hàm số \(y = \left| {\sin x} \right|\) có tập xác định D = R, suy ra có \(x \in R\) thì \( - x \in R\).
Mặt khác, \(f( - x) = \left| {\sin ( - x)} \right| = \left| { - \sin x} \right| = \sin x = f(x)\).
Vậy hàm số đáp án A là hàm số chẵn.
Nghiệm của phương trình \(\cos x = 0\) là?
- A.
\(x = k2\pi ,k \in \mathbb{Z}\)
- B.
\(x = k\pi ,k \in \mathbb{Z}\)
- C.
\(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
- D.
\(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\)
Đáp án : C
Nghiệm của phương trình lượng giác cơ bản.
\(\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Số hạng thứ 3 của dãy số \(\left\{ {\begin{array}{*{20}{c}}{{u_1} = 1}\\{{u_n} = 2{u_{n - 1}} + 3}\end{array}} \right.\) là?
- A.
5
- B.
8
- C.
28
- D.
13
Đáp án : D
Tìm lần lượt \({u_2},{u_3}\) bằng cách thay n vào công thức tổng quát.
Ta có:
\({u_2} = 2{u_{2 - 1}} + 3 = 2{u_1} + 3 = 2.1 + 3 = 5\)
\({u_3} = 2{u_{3 - 1}} + 3 = 2{u_2} + 3 = 2.5 + 3 = 13\)
Dãy số nào sau đây là cấp số cộng?
- A.
1; 4; 8; 10
- B.
2; 3; 5; 8; 9
- C.
0; 2; 4; 6; 8
- D.
1; 3; -5; -7; -9
Đáp án : C
Dãy số lập thành một cấp số cộng khi và chỉ khi hai phần tử liên tiếp sai khác nhau một hằng số.
Xét hiệu các phần tử liên tiếp trong các dãy số, chỉ có dãy ở đáp án C phần tử sau hơn phần tử liền trước 2 đơn vị (8 – 6 = 6 – 4 = 4 – 2 = 2 – 0 = 2).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 12\) và công bội \(q = - 2\). Số hạng thứ sáu của cấp số nhân đã cho bằng
- A.
2
- B.
-384
- C.
-24
- D.
-34
Đáp án : B
Sử dụng công thức \({u_n} = {u_1}{q^{n - 1}}\).
Ta có: \({u_6} = {u_1}{q^{6 - 1}} = 12.{( - 2)^5} = - 384\).
Số lượng khách hàng nữ mua bảo hiểm nhân thọ trong một ngày được thống kê trong bảng tần số ghép nhóm sau:

Giá trị đại diện của nhóm [30;40) là
- A.
40
- B.
30
- C.
35
- D.
9
Đáp án : C
Giá trị đại diện nhóm \([{a_m};{a_n})\) là: \(\frac{{{a_m} + {a_n}}}{2}\).
Ta có giá trị đại diện nhóm [30;40) là: \(\frac{{30 + 40}}{2} = 35\).
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng).

Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng sau đây?
- A.
[7;9)
- B.
[9;11)
- C.
[11;13)
- D.
[13;15)
Đáp án : B
Tính số trung bình của mẫu số liệu trên.
Ta có bảng sau:

Khi đó \(\overline x = \frac{{2.6 + 7.8 + 7.10 + 3.12 + 1.14}}{{20}} = 9,4\).
Số nghiệm của phương trình \(\sin 2x + \cos x = 0\) trên \([0;2\pi ]\) là
- A.
3
- B.
1
- C.
2
- D.
4
Đáp án : D
Biến đổi phương trình trở thành dạng phương trình tích, đưa về giải phương trình lượng giác cơ bản.
\(\sin 2x + \cos x = 0 \Leftrightarrow 2\sin x.\cos x + \cos x = 0 \Leftrightarrow \cos x.(2\sin x + 1) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{2\sin x + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{\sin x = - \frac{1}{2}}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = - \frac{\pi }{6} + k2\pi }\\{x = \frac{{7\pi }}{6} + k2\pi }\end{array}} \right.} \right.\) với \(k \in \mathbb{Z}\).
Vì \(x \in [0;2\pi ]\) nên chỉ có 4 nghiệm thỏa mãn: \(x = \left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\frac{{7\pi }}{6};\frac{{11\pi }}{6}} \right\}\).
Cho cấp số cộng \(({u_n})\) có \({u_5} = - 10\) và \({u_{15}} = 60\). Tổng 20 số hạng đầu tiên của cấp số cộng là
- A.
560
- B.
480
- C.
570
- D.
475
Đáp án : C
Tìm số hạng đầu và công sai dựa theo công thức \({u_n} = {u_1} + (n - 1)d\).
Từ đó tìm tổng 20 số hạng đầu tiên \({S_n} = \frac{{({u_1} + {u_n})n}}{2}\).
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{{u_5} = {u_1} + 4d}\\{{u_{15}} = {u_1} + 14d}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 10 = {u_1} + 4d}\\{60 = {u_1} + 14d}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{u_1} = - 38}\\{d = 7}\end{array}} \right.\)
Từ đó ta tính được \({u_{20}} = - 38 + (20 - 1)7 = 95\).
Vậy tổng 20 số hạng đầu của cấp số cộng là \({S_{20}} = \frac{{({u_1} + {u_{20}}).20}}{2} = \frac{{( - 38 + 95).20}}{2} = 570\).
Cho phương trình lượng giác \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0\). Khi đó
a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
a) Phương trình tương đương \(\sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \frac{\pi }{3}\)
b) Phương trình có nghiệm là \(x = \frac{\pi }{4} + k2\pi \); \(x = \frac{{7\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\)
c) Phương trình có nghiệm âm lớn nhất bằng \( - \frac{\pi }{4}\)
d) Số nghiệm của phương trình trong khoảng \(( - \pi ;\pi )\) là hai nghiệm
Giải phương trình lượng giác \(\sin x = a\):
- Nếu \(\left| a \right| > 1\) thì phương trình vô nghiệm.
- Nếu \(\left| a \right| \le 1\) thì chọn cung \(\alpha \) sao cho \(\sin \alpha = a\). Khi đó phương trình trở thành:
\(\sin x = \sin \alpha \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = \pi - \alpha + k2\pi }\end{array}} \right.\) với \(k \in \mathbb{Z}\).
\(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - \frac{\pi }{{12}} = - \frac{\pi }{3} + k2\pi }\\{x - \frac{\pi }{{12}} = \pi + \frac{\pi }{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \frac{\pi }{4} + k2\pi }\\{x = \frac{{17\pi }}{{12}} + k2\pi }\end{array}} \right.\)
a)Sai. \(2\sin \left( {x - \frac{\pi }{{12}}} \right) + \sqrt 3 = 0 \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = - \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin \left( {x - \frac{\pi }{{12}}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\)
b) Sai. Phương trình có nghiệm là \(x = - \frac{\pi }{4} + k2\pi \); \(x = \frac{{17\pi }}{{12}} + k2\pi \) \((k \in \mathbb{Z})\).
c) Đúng.
+ Xét họ nghiệm \(x = - \frac{\pi }{4} + k2\pi \):
Nghiệm âm lớn nhất là \(x = - \frac{\pi }{4}\) khi k = 0.
+ Xét họ nghiệm \(x = \frac{{17\pi }}{{12}} + k2\pi \):
Nghiệm âm lớn nhất là \(x = - \frac{{7\pi }}{{12}}\) khi k = -1.
Vì \( - \frac{\pi }{4} > - \frac{{7\pi }}{{12}}\) nên nghiệm âm lớn nhất là \(x = - \frac{\pi }{4}\).
d) Đúng.
+ Xét họ nghiệm \(x = - \frac{\pi }{4} + k2\pi \):
\( - \pi < x < \pi \Leftrightarrow - \pi < - \frac{\pi }{4} + k2\pi < \pi \)
\( \Leftrightarrow - 1 < - \frac{1}{4} + 2k < 1 \Leftrightarrow - \frac{3}{4} < 2k < \frac{5}{4} \Leftrightarrow - \frac{3}{8} < k < \frac{5}{8}\).
Vậy chỉ có k = 0 thỏa mãn. Khi đó \(x = - \frac{\pi }{4}\).
+ Xét họ nghiệm \(x = \frac{{17\pi }}{{12}} + k2\pi \):
\( - \pi < x < \pi \Leftrightarrow - \pi < \frac{{17\pi }}{{12}} + k2\pi < \pi \Leftrightarrow - 1 < \frac{{17}}{{12}} + 2k < 1\)
\( \Leftrightarrow - \frac{{29}}{{12}} < 2k < - \frac{5}{{12}} \Leftrightarrow - \frac{{29}}{{24}} < k < - \frac{5}{{24}}\).
Vậy chỉ có k = -1 thỏa mãn. Khi đó \(x = - \frac{{7\pi }}{{12}}\).
Vậy phương trình có hai nghiệm thuộc khoảng \(( - \pi ;\pi )\) là \(x = - \frac{\pi }{4}\) và \(x = - \frac{{7\pi }}{{12}}\).
Cho \(\cos \alpha = - \frac{1}{4}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\). Khi đó
a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
c) \(\tan \alpha = \sqrt {15} \)
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
a) \({\sin ^2}\alpha = \frac{{15}}{{16}}\)
b) \(\sin \alpha = \frac{{\sqrt {15} }}{4}\)
c) \(\tan \alpha = \sqrt {15} \)
d) \(\cot \alpha = - \frac{1}{{\sqrt {15} }}\)
a) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu.
b) Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) và dựa vào góc phần tư của đường tròn lượng giác để xét dấu.
c) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{1}{{\cot \alpha }}\)
d) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\tan \alpha }}\)
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( { - \frac{1}{4}} \right)^2} = \frac{{15}}{{16}} \Rightarrow \sin \alpha = \pm \frac{{\sqrt {15} }}{4}\).
Vì \(\pi < \alpha < \frac{{3\pi }}{2}\) nên điểm cuối của cung \(\alpha \) thuộc góc phần tư thứ III nên \(\sin \alpha < 0\). Vậy \(\sin \alpha = - \frac{{\sqrt {15} }}{4}\).
\(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{ - \frac{1}{4}}}{{ - \frac{{\sqrt {15} }}{4}}} = \sqrt {15} \); \(\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{1}{{\sqrt {15} }}\).
a)Đúng.
b) Sai.
c) Đúng.
d) Sai.
Cho dãy số \(({u_n})\) biết \({u_n} = {2^n} + 1\). Khi đó
a) Dãy số \(({u_n})\) là dãy số tăng
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_6} = 65\)
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
a) Dãy số \(({u_n})\) là dãy số tăng
b) Dãy số \(({u_n})\) là dãy số bị chặn
c) \({u_6} = 65\)
d) Số hạng thứ n + 2 của dãy số là \({u_{n + 2}} = {2^n}.2\)
a) Dãy số \(({u_n})\) là dãy số giảm nếu \({u_n} > {u_{n + 1}}\). Dãy số \(({u_n})\) là dãy số tăng nếu \({u_n} < {u_{n + 1}}\).
b) Dãy số \(({u_n})\) là dãy số bị chặn nếu \(({u_n})\) vừa bị chặn trên vừa bị chặn dưới, tức tồn tại hai số m, M sao cho \(m \le {u_n} \le M\) \(\forall n \in \mathbb{N}*\).
c) Tính \({u_6}\) bằng công thức \({u_n} = {2^n} + 1\).
d) Thay n + 2 vào n trong công thức số hạng tổng quát \({u_n} = {2^n} + 1\).
a) Đúng. \({u_{n + 1}} - {u_n} = {2^{n + 1}} + 1 - ({2^n} + 1) = {2^{n + 1}} - {2^n} = {2^n}(2 - 1) = {2^n} > 0\) với mọi n. Vậy dãy số là dãy tăng.
b) Sai. Dãy không bị chặn trên vì không có giá trị M nào để \({2^n} < M\) với mọi n. Vậy dãy số không bị chặn.
c) Đúng. \({u_6} = {2^6} + 1 = 64 + 1 = 65\).
d) Sai. \({u_{n + 2}} = {2^{n + 2}} + 1 = {4.2^n} + 1\).
Kết quả khảo sát cân nặng của 25 quả cam ở mỗi lô hàng A, B được cho ở bảng sau:

a) Giá trị đại diện của nhóm [150;155) bằng 152,5
b) Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [155;160)
c) Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [160;165)
d) Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A
a) Giá trị đại diện của nhóm [150;155) bằng 152,5
b) Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [155;160)
c) Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [160;165)
d) Theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A
a) Giá trị đại diện nhóm \([{a_m};{a_n})\) là: \(\frac{{{a_m} + {a_n}}}{2}\).
b) Nhóm chứa mốt có tần số cao nhất.
c) Nhóm chứa mốt có tần số cao nhất.
d) Tính cân nặng trung bình của mỗi lô hàng rồi so sánh.
a) Đúng. Giá trị đại diện nhóm [150;155) là \(\frac{{150 + 155}}{2} = 152,5\).
b) Sai. Nhóm chứa mốt của mẫu số liệu ở lô hàng A là [160;165) vì có tần số cao nhất là 12.
c) Sai. Nhóm chứa mốt của mẫu số liệu ở lô hàng B là [165;170) vì có tần số cao nhất là 10.
d) Đúng. Bảng thống kê số lượng cam theo giá trị đại diện:

Cân nặng trung bình của mỗi quả cam ở lô A là:
\(\overline {{x_A}} = \frac{{152,5.2 + 157,5.6 + 162,5.12 + 167,5.4 + 172,5.1}}{{25}} = 161,7\) (gam).
Cân nặng trung bình của mỗi quả cam ở lô B là:
\(\overline {{x_B}} = \frac{{152,5.1 + 157,5.3 + 162,5.7 + 167,5.10 + 172,5.4}}{{25}} = 165,1\) (gam).
Thấy \(\overline {{x_A}} < \overline {{x_B}} \). Vậy nếu so sánh theo số trung bình thì cam ở lô hàng B nặng hơn cam ở lô hàng A.
Hằng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu h (m) của mực nước theo thời gian t (giờ) trong một ngày được cho bởi công thức \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) với \(0 \le t \le 24\). Tính thời điểm mực nước tại cảng cao nhất.
Đáp án:
Đáp án:
Tìm t sao cho hàm số \(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) đạt giá trị lớn nhất.
\(h = 11 + 2\sin \left( {\frac{\pi }{{12}}t} \right)\) đạt giá trị lớn nhất khi \(\sin \left( {\frac{\pi }{{12}}t} \right) = 1 \Leftrightarrow \frac{\pi }{{12}}t = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 6 + 24k\) (giờ).
Vì \(0 \le t \le 24\) nên chỉ có giá trị t = 6 thỏa mãn.
Vậy thời điểm mực nước tại cảng cao nhất là lúc 6 giờ.
Phương trình \(2\sin 2x + 4\cos x = 0\) có bao nhiêu nghiệm trong khoảng (0;3000)?
Đáp án:
Đáp án:
Giải phương trình lượng giác bằng cách biến đổi về dạng phương trình tích. Xét họ nghiệm trong khoảng (0;3000) để tìm số giá trị k nguyên thỏa mãn.
Ta có: \(2\sin 2x + 4\cos x = 0 \Rightarrow 4\sin x.\cos x + 4\cos x = 0 \Rightarrow 4\cos x.(\sin x + 1) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos x = 0}\\{\sin x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{2} + k\pi }\\{x = \frac{{3\pi }}{2} + k2\pi }\end{array}} \right. \Leftrightarrow x = \frac{\pi }{2} + k\pi \) với \(k \in \mathbb{Z}\).
Xét họ nghiệm \(x = \frac{\pi }{2} + k\pi \), ta có:
\(0 < \frac{\pi }{2} + k\pi < 3000 \Leftrightarrow - \frac{\pi }{2} < k\pi < 3000 - \frac{\pi }{2} \Leftrightarrow - \frac{1}{2} < k < \frac{{3000}}{\pi } - \frac{1}{2} \Leftrightarrow - 0,5 < k < 954,43\).
Mà \(k \in \mathbb{Z}\) nên \(k \in \{ 0;1;2;3;...;954\} \), tức có 955 giá trị k thỏa mãn.
Vậy phương trình có 955 nghiệm thuộc khoảng (0;3000).
Công ty cây xanh X trồng 496 cây hoa trong một khu vườn hình tam giác như sau: hàng thứ nhất trồng 1 cây hoa, kể từ hàng thứ hai trở đi số cây hoa trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi công ty cây xanh X trồng được bao nhiêu hàng cây trong khu vườn hình tam giác đó.
Đáp án:
Đáp án:
Số cây mỗi hàng lập thành một cấp số cộng với tổng n số hạng là 496, số hạng đầu \({u_1} = 1\) công sai d = 1. Tìm n.
Số cây mỗi hàng lập thành một cấp số cộng với tổng n số hạng là 496, số hạng đầu \({u_1} = 1\) công sai d = 1.
Ta có: \(496 = \frac{{2.1 + (n - 1).1}}{2}.n \Leftrightarrow 992 = (2 + n - 1).n = {n^2} + n - 992 = 0\).
Ta tính được n = 31 hoặc n = -32 (loại).
Vậy số hàng cây trồng được là 31 hàng.
Cho dãy số \(({u_n})\) biết \({u_n} = n + \frac{1}{n}\). Tìm m để dãy số \(({u_n})\) bị chặn dưới bởi m.
Đáp án:
Đáp án:
Chứng minh dãy số tăng và bị chặn dưới tại \(m = {u_1}\).
Xét \({u_{n + 1}} - {u_n} = \left( {n + 1 + \frac{1}{{n + 1}}} \right) - \left( {n + \frac{1}{n}} \right) = 1 + \frac{1}{{n + 1}} - \frac{1}{n} = \left( {1 - \frac{1}{n}} \right) + \frac{1}{{n + 1}}\).
Ta có: \(n \ge 1 \Leftrightarrow \frac{1}{n} < 1 \Leftrightarrow 1 - \frac{1}{n} > 0\); \(n \ge 1 \Rightarrow \frac{1}{{n + 1}} > 0\).
Vậy \({u_{n + 1}} - {u_n} > 0\), tức dãy số tăng.
Khi đó, dãy bị chặn dưới bởi \({u_1} = 1 + \frac{1}{1} = 2 = m\).
Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 50 học sinh lớp 11A.

Số học sinh có chiều cao bao nhiêu cm là nhiều nhất (làm tròn đến hàng đơn vị)?
Đáp án:
Đáp án:
Tìm mốt của mẫu số liệu.
Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: [aj; aj+1).
Bước 2: Mốt được xác định là
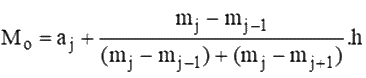
trong đó mj là tần số của nhóm j (quy ước mo = mk+1 = 0) và h là độ dài của nhóm.
Tần số lớn nhất là 14 nên nhóm chứa mốt là nhóm [150;155).
Ta có \({M_o} = 150 + \frac{{14 - 7}}{{(14 - 7) + (14 - 10)}}(155 - 150) \approx 153\).
Vậy số học sinh có chiều cao khoảng 153 cm là nhiều nhất.
Trong một hội thao, thời gian chạy 200 m của một nhóm vận động viên được ghi lại trong bảng sau:

Dựa vào bảng dữ liệu trên, ban tổ chức muốn chọn ra khoảng 50% số vận động viên chạy nhanh nhất để tiếp tục thi vòng 2. Ban tổ chức nên chọn các vận động viên có thời gian chạy không quá bao nhiêu giây (kết quả làm tròn đến hàng phần mười)?
Đáp án:
Đáp án:
Tìm trung vị của mẫu số liệu trên.
Bước 1: Xác định nhóm chứa trung vị. Giả sử đó là nhóm thứ p: [ap; ap+1).
Bước 2: Trung vị
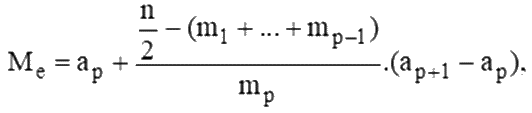
trong đó n là cỡ mẫu, mp là tần số nhóm p. Với p = 1, ta quy ước m1 + ….+ mp-1 = 0.
Cỡ mẫu là n = 5 + 12 +32 + 45 + 30 = 124.
Gọi \({x_1};{x_2};...;{x_{124}}\) là thời gian chạy của 124 vận động viên tham gia hội thao và giả sử dãy này được sắp xếp theo thứ tự tăng dần.
Khi đó, trung vị là \(\frac{{{x_{62}} + {x_{63}}}}{2}\). Do giá trị \({x_{62}},{x_{63}}\) thuộc nhóm [22,5;23) nên nhóm này chứa trung vị.
Trung vị là \({M_e} = 22,5 + \frac{{\frac{{124}}{2} - (5 + 12 + 32)}}{{45}}.(23 - 22,5) \approx 22,6\).
Vậy ban tổ chức nên chọn vận động viên có thời gian chạy không quá 22,6 giây.
Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8: Tổng quan và Hướng dẫn ôn tập
Chào mừng các em học sinh lớp 11 đến với bài viết tổng hợp và phân tích chi tiết về Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8. Đây là một đề thi quan trọng, giúp các em làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và đánh giá mức độ nắm vững kiến thức đã học trong giai đoạn đầu năm học.
Cấu trúc đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8
Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8 thường bao gồm các dạng câu hỏi sau:
- Câu hỏi trắc nghiệm: Kiểm tra kiến thức cơ bản, khả năng nhận biết và vận dụng các khái niệm, định lý.
- Câu hỏi tự luận: Yêu cầu học sinh trình bày lời giải chi tiết, vận dụng kiến thức để giải quyết các bài toán cụ thể.
Các chủ đề thường xuất hiện trong đề thi bao gồm:
- Hàm số bậc hai
- Bất phương trình bậc hai
- Phương trình lượng giác cơ bản
- Đạo hàm
- Ứng dụng đạo hàm để khảo sát hàm số
Hướng dẫn ôn tập hiệu quả cho đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8
Để đạt kết quả tốt nhất trong kỳ thi giữa kì 1, các em cần có kế hoạch ôn tập khoa học và hiệu quả. Dưới đây là một số gợi ý:
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các khái niệm, định lý và công thức quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau, từ dễ đến khó, để rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập thường gặp.
- Ôn tập theo chủ đề: Chia nhỏ kiến thức thành các chủ đề nhỏ, ôn tập từng chủ đề một cách kỹ lưỡng.
- Làm đề thi thử: Giải các đề thi thử để làm quen với cấu trúc đề thi, thời gian làm bài và rèn luyện khả năng làm bài thi.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn trong quá trình ôn tập, hãy hỏi thầy cô giáo, bạn bè hoặc tìm kiếm sự giúp đỡ trên các diễn đàn, trang web học tập trực tuyến.
Đáp án và lời giải chi tiết Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8
tusach.vn cung cấp đáp án và lời giải chi tiết cho Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8. Các em có thể tham khảo để kiểm tra lại kết quả làm bài của mình và hiểu rõ hơn về cách giải các bài toán.
Tải đề thi và đáp án
Các em có thể tải Đề thi giữa kì 1 Toán 11 Kết nối tri thức - Đề số 8 và đáp án tại đây: [Link tải đề thi]
Lời khuyên
Hãy dành thời gian ôn tập kỹ lưỡng và làm bài thi một cách tự tin. Chúc các em đạt kết quả tốt nhất trong kỳ thi giữa kì 1!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Hàm số bậc hai | Cao |
| Bất phương trình bậc hai | Trung bình |
| Phương trình lượng giác cơ bản | Trung bình |
| Đạo hàm | Cao |
| Nguồn: tusach.vn | |