Đề thi học kì 2 Toán 12 Chân trời sáng tạo - Đề số 2
Tổng quan nội dung
Đề thi học kì 2 Toán 12 Chân trời sáng tạo - Đề số 2
Tusach.vn xin giới thiệu Đề thi học kì 2 Toán 12 Chân trời sáng tạo - Đề số 2, được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo.
Đề thi này là tài liệu ôn tập lý tưởng, giúp học sinh làm quen với các dạng bài tập thường gặp và rèn luyện kỹ năng giải đề. Đi kèm với đề thi là đáp án chi tiết, giúp học sinh tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Đề bài
Họ nguyên hàm của hàm số f(x) = 2x + 1 là
- A.
\({x^2} + 1 + C\)
- B.
\({x^2} + x + C\)
- C.
\({x^2} + C\)
- D.
\(2x + C\)
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) trên \(\mathbb{R}\). Các mệnh đề sau, mệnh đề nào sai?
- A.
\(\int {f(x)dx} = F(x) + C\)
- B.
\(\left( {\int {f(x)dx} } \right)' = f(x)\)
- C.
\(\left( {\int {f(x)dx} } \right)' = f(x) + C\)
- D.
\(\left( {\int {f(x)dx} } \right)' = F'(x)\)
Mệnh đề nào dưới đây đúng?
- A.
\(\int {\cos xdx} = \sin x + C\)
- B.
\(\int {\cos xdx} = - \sin x + C\)
- C.
\(\int {\cos xdx} = - \cos x + C\)
- D.
\(\int {\cos xdx} = \frac{1}{2}{\cos ^2}x + C\)
Cho \(\int\limits_2^3 {f(x)dx} = 1\) và \(\int\limits_2^3 {g(x)dx} = 4\). Khi đó \(\int\limits_2^3 {\left[ {f(x) + g(x)} \right]dx} \) bằng
- A.
5
- B.
3
- C.
-3
- D.
4
Diện tích S của hình phẳng giới hạn bởi các đường thẳng \(y = {x^2}\), y = -1, x = 0, x = 1 được tính bởi công thức nào sau đây?
- A.
\(S = \int\limits_0^1 {\left( {{x^2} + 1} \right)dx} \)
- B.
\(S = \pi \int\limits_0^1 {\left( {{x^2} + 1} \right)dx} \)
- C.
\(S = \int\limits_0^1 {{{\left( {{x^2} + 1} \right)}^2}dx} \)
- D.
\(S = \pi \int\limits_0^1 {\left| {{x^2} - 1} \right|dx} \)
Trong không gian Oxyz, mặt phẳng (P): x – y + z – 1 = 0 có một vecto pháp tuyến là
- A.
\(\overrightarrow {{n_1}} = \left( { - 1;1;1} \right)\)
- B.
\(\overrightarrow {{n_2}} = \left( {1; - 1;1} \right)\)
- C.
\(\overrightarrow {{n_3}} = \left( {1;1;1} \right)\)
- D.
\(\overrightarrow {{n_4}} = \left( {1;1; - 1} \right)\)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d đi qua điểm M(1;1;1) và nhận vecto \(\overrightarrow u = (2;3;4)\) làm vecto chỉ phương. Phương trình tham số của d là
- A.
\(\left\{ \begin{array}{l}x = 1 + 4t\\y = 1 + 3t\\z = 1 + 2t\end{array} \right.\) \((t \in \mathbb{R})\)
- B.
\(\left\{ \begin{array}{l}x = - 1 + 2t\\y = - 1 + 3t\\z = - 1 + 4t\end{array} \right.\) \((t \in \mathbb{R})\)
- C.
\(\left\{ \begin{array}{l}x = - 1 - 2t\\y = - 1 - 3t\\z = - 1 - 4t\end{array} \right.\) \((t \in \mathbb{R})\)
- D.
\(\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 + 3t\\z = 1 + 4t\end{array} \right.\) \((t \in \mathbb{R})\)
Trong không gian Oxyz, xác định tâm I và bán kính R của mặt cầu có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z + 2} \right)^2} = 9\).
- A.
I(1;4;-2); R = 3
- B.
I(-1;-4;2); R = 3
- C.
I(1;4;-2); R = 9
- D.
I(-1;-4;2); R = 9
Trong không gian Oxyz, cho mặt phẳng (P): x + 2y + 2z + 3 = 0 và mặt phẳng (Q): 3x – 4y + 5 = 0. Gọi \(\alpha \) là góc giữa hai mặt phẳng (P) và (Q). Tính giá trị \(\cos \alpha \).
- A.
\(\cos \alpha = \frac{{11}}{{15}}\)
- B.
\(\cos \alpha = - \frac{1}{3}\)
- C.
\(\cos \alpha = - \frac{{11}}{{15}}\)
- D.
\(\cos \alpha = \frac{1}{3}\)
Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng d: \(\left\{ \begin{array}{l}x = 3 + 2t\\y = 1 - 3t\\z = - 1 + t\end{array} \right.\)?
- A.
\({M_1}\left( {3;1; - 1} \right)\)
- B.
\({M_2}\left( {2; - 3;1} \right)\)
- C.
\({M_3}\left( {1;3; - 1} \right)\)
- D.
\({M_4}\left( { - 3; - 1;1} \right)\)
Cho hai biến cố A, B với P(A) = 0,3, P(B) = 0,6, \(P(A \cap B) = 0,2\). Xác suất P(A|B) là
- A.
\(\frac{1}{2}\)
- B.
\(\frac{1}{3}\)
- C.
\(\frac{2}{3}\)
- D.
\(\frac{1}{6}\)
Gieo con xúc xắc 1 lần. Gọi A là biến cố xuất hiện mặt 2 chấm. B là biến cố xuất hiện mặt chẵn. Xác suất \(P\left( {A|B} \right)\) là
- A.
\(\frac{1}{2}\)
- B.
\(\frac{1}{3}\)
- C.
\(\frac{2}{3}\)
- D.
\(\frac{1}{6}\)
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x – 2y + 2z – 2 = 0 và điểm I(-1;2;-1). Biết mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có diện tích là \(25\pi \).
a) Bán kính đường tròn (C) là r = 5.
b) Khoảng cách từ I đến mặt phẳng (P) là 3.
c) Tâm đường tròn (C) có tọa độ là H(1;3;1).
d) Phương trình mặt cầu (S) là \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 16\).
Lớp 11A1 có 45 học sinh, trong đó có 25 học sinh tham gia câu lạc bộ Tiếng Anh, 16 học sinh tham gia câu lạc bộ Nhảy, 12 học sinh vừa tham gia câu lạc bộ Tiếng Anh vừa tham gia câu lạc bộ Nhảy. Chọn ngẫu nhiên 1 học sinh. Xét các biến cố sau:
A: “Học sinh được chọn tham gia câu lạc bộ Tiếng Anh”.
B: “Học sinh được chọn tham gia câu lạc bộ Nhảy”.
a) \(P\left( A \right) = \frac{5}{{10}}\).
b) \(P\left( B \right) = \frac{7}{{20}}\).
c) \(P\left( {A|B} \right) = 0,75\).
d) Xác suất chọn được học sinh tham gia câu lạc bộ Nhảy, biết học sinh đó tham gia câu lạc bộ Tiếng Anh là 0,48.
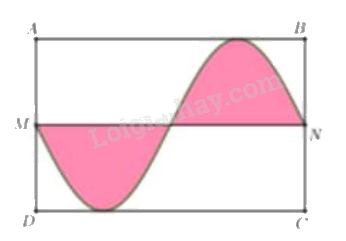
Một mảnh đất hình chữ nhật ABCD được quy hoạch như hình bên. Biết đường cong là đường hình sin của hàm số dạng y = asin(bx). Biết AB = \(2\pi \) (m) và AD = 4 (m). Phần tô đậm (giới hạn bởi đường cong và đoạn MN) được sử dụng để trồng hoa. Tính diện tích phần còn lại của mảnh vườn (đơn vị: \({m^2}\), làm tròn đến hàng phần chục).
Chuồng I có 5 con gà mái, 2 con gà trống. Chuồng II có 3 con gà mái, 5 con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: “Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho 3 thì bác chọn chuồng I. Nếu số chấm không chia hết cho 3 thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà”. Tính xác suất để bác Mai bắt được con gà mái (kết quả làm tròn đến hàng phần trăm).
Một ô tô đang di chuyển với tốc độ 20 m/s thì hãm phanh nên tốc độ (m/s) của xe thay đổi theo thời gian t (giây) được tính theo công thức v(t) = 20 – 5t \((0 \le t \le 4)\). Kể từ lúc hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?
Công nghệ hỗ trợ trọng tài VAR (Video Assistant Referee) thiết lập một hệ tọa độ Oxyz để theo dõi vị trí của quả bóng M. Cho biết M đang nằm trên mặt sân có phương trình z = 0 đồng thời thuộc mặt cầu \((S):{\left( {x - 32} \right)^2} + {\left( {y - 50} \right)^2} + {\left( {z - 10} \right)^2} = 109\) (đơn vị độ dài tính theo mét). Gọi J là hình chiếu vuông góc của tâm I mặt cầu trên mặt sân. Khoảng cách từ vị trí M của quả bóng đến điểm J bằng bao nhiêu?
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {(x - 2)^2} - 1\), trục hoành và hai đường thẳng x = 1, x = 2 bằng bao nhiêu?
Trong không gian tọa độ (Oxyz), cho điểm M(1;2;-2) và mặt phẳng (P): 2x + y – 3z + 1 = 0. Phương trình của đường thẳng đi qua điểm M và vuông góc với (P) có phương trình tham số: \(\left\{ \begin{array}{l}x = 1 - 4t\\y = 2 + bt\\z = - 2 + ct\end{array} \right.\;\left( {t \in \mathbb{R}} \right)\). Khi đó giá trị của biểu thức \(P = {b^2} + {c^2}\) là bao nhiêu?
Trong một khu du lịch, người ta cho du khách trải nghiệm thiên nhiên bằng cách đu theo đường trượt zipline từ vị trí A cao 15 m của tháp 1 này sang vị trí B cao 10 m của tháp 2 trong khung cảnh tuyệt đẹp xung quanh. Với hệ trục toạ độ Oxyz cho trước (đơn vị: mét), toạ độ của A và B lần lượt là (3; 2,5; 15) và (21; 27,5; 10). Xác định toạ độ của du khách khi ở độ cao 12 mét.

Lời giải và đáp án
Họ nguyên hàm của hàm số f(x) = 2x + 1 là
- A.
\({x^2} + 1 + C\)
- B.
\({x^2} + x + C\)
- C.
\({x^2} + C\)
- D.
\(2x + C\)
Đáp án : B
Áp dụng công thức nguyên hàm của hàm số lũy thừa \(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}} + C\).
\(\int {(2x + 1)dx} = 2.\frac{{{x^2}}}{2} + x + C = {x^2} + x + C\).
Cho hàm số F(x) là một nguyên hàm của hàm số f(x) trên \(\mathbb{R}\). Các mệnh đề sau, mệnh đề nào sai?
- A.
\(\int {f(x)dx} = F(x) + C\)
- B.
\(\left( {\int {f(x)dx} } \right)' = f(x)\)
- C.
\(\left( {\int {f(x)dx} } \right)' = f(x) + C\)
- D.
\(\left( {\int {f(x)dx} } \right)' = F'(x)\)
Đáp án : C
Áp dụng định nghĩa nguyên hàm.
Với F(x) là một nguyên hàm của hàm số f(x) trên \(\mathbb{R}\): \(F'(x) = f(x)\) và \(\int {f(x)dx} = F(x) + C\).
Vậy A đúng.
Ta có: \(\left( {\int {f(x)dx} } \right)' = \left( {F(x) + C} \right)' = F'(x) = f(x)\).
Vậy B, D đúng, C sai.
Mệnh đề nào dưới đây đúng?
- A.
\(\int {\cos xdx} = \sin x + C\)
- B.
\(\int {\cos xdx} = - \sin x + C\)
- C.
\(\int {\cos xdx} = - \cos x + C\)
- D.
\(\int {\cos xdx} = \frac{1}{2}{\cos ^2}x + C\)
Đáp án : A
Áp dụng công thức nguyên hàm của hàm số lượng giác.
Ta có:\(\int {\cos xdx} = \sin x + C\).
Cho \(\int\limits_2^3 {f(x)dx} = 1\) và \(\int\limits_2^3 {g(x)dx} = 4\). Khi đó \(\int\limits_2^3 {\left[ {f(x) + g(x)} \right]dx} \) bằng
- A.
5
- B.
3
- C.
-3
- D.
4
Đáp án : A
Áp dụng tính chất của tích phân.
\(\int\limits_2^3 {\left[ {f(x) + g(x)} \right]dx} = \int\limits_2^3 {f(x)dx} + \int\limits_2^3 {g(x)dx} = 1 + 4 = 5\).
Diện tích S của hình phẳng giới hạn bởi các đường thẳng \(y = {x^2}\), y = -1, x = 0, x = 1 được tính bởi công thức nào sau đây?
- A.
\(S = \int\limits_0^1 {\left( {{x^2} + 1} \right)dx} \)
- B.
\(S = \pi \int\limits_0^1 {\left( {{x^2} + 1} \right)dx} \)
- C.
\(S = \int\limits_0^1 {{{\left( {{x^2} + 1} \right)}^2}dx} \)
- D.
\(S = \pi \int\limits_0^1 {\left| {{x^2} - 1} \right|dx} \)
Đáp án : A
Áp dụng công thức tính diện tích hình phẳng: \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \).
Ta có \({x^2} + 1 > 0\) nên \(\left| {{x^2} + 1} \right| = {x^2} + 1\).
\(S = \int\limits_0^1 {\left| {{x^2} - ( - 1)} \right|dx} = \int\limits_0^1 {\left| {{x^2} + 1} \right|dx} = \int\limits_0^1 {\left( {{x^2} + 1} \right)dx} \).
Trong không gian Oxyz, mặt phẳng (P): x – y + z – 1 = 0 có một vecto pháp tuyến là
- A.
\(\overrightarrow {{n_1}} = \left( { - 1;1;1} \right)\)
- B.
\(\overrightarrow {{n_2}} = \left( {1; - 1;1} \right)\)
- C.
\(\overrightarrow {{n_3}} = \left( {1;1;1} \right)\)
- D.
\(\overrightarrow {{n_4}} = \left( {1;1; - 1} \right)\)
Đáp án : B
Mặt phẳng Ax + By + Cz + D = 0 có một vecto pháp tuyến là \(\overrightarrow n = (A;B;C)\).
Mặt phẳng (P): x – y + z – 1 = 0 có một vecto pháp tuyến là \(\overrightarrow {{n_2}} = \left( {1; - 1;1} \right)\).
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d đi qua điểm M(1;1;1) và nhận vecto \(\overrightarrow u = (2;3;4)\) làm vecto chỉ phương. Phương trình tham số của d là
- A.
\(\left\{ \begin{array}{l}x = 1 + 4t\\y = 1 + 3t\\z = 1 + 2t\end{array} \right.\) \((t \in \mathbb{R})\)
- B.
\(\left\{ \begin{array}{l}x = - 1 + 2t\\y = - 1 + 3t\\z = - 1 + 4t\end{array} \right.\) \((t \in \mathbb{R})\)
- C.
\(\left\{ \begin{array}{l}x = - 1 - 2t\\y = - 1 - 3t\\z = - 1 - 4t\end{array} \right.\) \((t \in \mathbb{R})\)
- D.
\(\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 + 3t\\z = 1 + 4t\end{array} \right.\) \((t \in \mathbb{R})\)
Đáp án : D
Đường thẳng đi qua điểm \(M({x_0};{y_0};{z_0})\) có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) có phương trình là \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\) \((t \in \mathbb{R})\).
d đi qua điểm M(1;1;1) có vecto chỉ phương \(\overrightarrow u = (2;3;4)\) có phương trình là \(\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 + 3t\\z = 1 + 4t\end{array} \right.\) \((t \in \mathbb{R})\).
Trong không gian Oxyz, xác định tâm I và bán kính R của mặt cầu có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z + 2} \right)^2} = 9\).
- A.
I(1;4;-2); R = 3
- B.
I(-1;-4;2); R = 3
- C.
I(1;4;-2); R = 9
- D.
I(-1;-4;2); R = 9
Đáp án : A
Mặt cầu phương trình \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm I(a;b;c), bán kính R.
Mặt cầu phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 4} \right)^2} + {\left( {z + 2} \right)^2} = 9\) có tâm I(1;4;-2), bán kính R = 3.
Trong không gian Oxyz, cho mặt phẳng (P): x + 2y + 2z + 3 = 0 và mặt phẳng (Q): 3x – 4y + 5 = 0. Gọi \(\alpha \) là góc giữa hai mặt phẳng (P) và (Q). Tính giá trị \(\cos \alpha \).
- A.
\(\cos \alpha = \frac{{11}}{{15}}\)
- B.
\(\cos \alpha = - \frac{1}{3}\)
- C.
\(\cos \alpha = - \frac{{11}}{{15}}\)
- D.
\(\cos \alpha = \frac{1}{3}\)
Đáp án : D
Hai mặt phẳng (P), (Q) có vecto pháp tuyến lần lượt là \(\overrightarrow n ,\overrightarrow {n'} \) có \(\cos \left( {(P),(Q)} \right) = \frac{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow {n'} } \right|}}\).
Vecto pháp tuyến của (P), (Q) lần lượt là \({\rm{\;}}\overrightarrow n = (1;2;2)\) và \(\overrightarrow {n'} {\rm{\;}} = (3; - 4;0)\).
\(\cos \alpha = \frac{{\left| {\overrightarrow n .\overrightarrow {n'} } \right|}}{{\left| {\overrightarrow n } \right|.\left| {\overrightarrow {n'} } \right|}} = \frac{{\left| {1.3 + 2.( - 4) + 2.0} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} .\sqrt {{3^2} + {{( - 4)}^2} + {0^2}} }} = \frac{1}{3}\).
Trong không gian Oxyz, điểm nào dưới đây thuộc đường thẳng d: \(\left\{ \begin{array}{l}x = 3 + 2t\\y = 1 - 3t\\z = - 1 + t\end{array} \right.\)?
- A.
\({M_1}\left( {3;1; - 1} \right)\)
- B.
\({M_2}\left( {2; - 3;1} \right)\)
- C.
\({M_3}\left( {1;3; - 1} \right)\)
- D.
\({M_4}\left( { - 3; - 1;1} \right)\)
Đáp án : A
Thay tọa độ từng điểm vào phương trình của d, nếu tìm được một giá trị t thỏa mãn hệ phương trình thì điểm đó thuộc d.
Với \({M_1}\left( {3;1; - 1} \right)\), ta có \(\left\{ \begin{array}{l}3 = 3 + 2t\\1 = 1 - 3t\\ - 1 = - 1 + t\end{array} \right. \Leftrightarrow t = 0\). Vậy \({M_1}\left( {3;1; - 1} \right) \in d\).
Cho hai biến cố A, B với P(A) = 0,3, P(B) = 0,6, \(P(A \cap B) = 0,2\). Xác suất P(A|B) là
- A.
\(\frac{1}{2}\)
- B.
\(\frac{1}{3}\)
- C.
\(\frac{2}{3}\)
- D.
\(\frac{1}{6}\)
Đáp án : B
Áp dụng công thức tính xác suất có điều kiện: \(P(A|B) = \frac{{P(A \cap B)}}{{P(B)}}\).
Áp dụng công thức: \(P(A|B) = \frac{{P(A \cap B)}}{{P(B)}} = \frac{{0,2}}{{0,6}} = \frac{1}{3}\).
Gieo con xúc xắc 1 lần. Gọi A là biến cố xuất hiện mặt 2 chấm. B là biến cố xuất hiện mặt chẵn. Xác suất \(P\left( {A|B} \right)\) là
- A.
\(\frac{1}{2}\)
- B.
\(\frac{1}{3}\)
- C.
\(\frac{2}{3}\)
- D.
\(\frac{1}{6}\)
Đáp án : B
Áp dụng công thức tính xác suất có điều kiện: \(P(A|B) = \frac{{P(A \cap B)}}{{P(B)}}\).
Vì \(A \subset B \Rightarrow P(A \cap B) = P(A) = \frac{1}{6}\).
Áp dụng công thức: \(P(A|B) = \frac{{P(A \cap B)}}{{P(B)}} = \frac{{\frac{1}{6}}}{{\frac{1}{2}}} = \frac{1}{3}\).
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng (P): x – 2y + 2z – 2 = 0 và điểm I(-1;2;-1). Biết mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có diện tích là \(25\pi \).
a) Bán kính đường tròn (C) là r = 5.
b) Khoảng cách từ I đến mặt phẳng (P) là 3.
c) Tâm đường tròn (C) có tọa độ là H(1;3;1).
d) Phương trình mặt cầu (S) là \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 16\).
a) Bán kính đường tròn (C) là r = 5.
b) Khoảng cách từ I đến mặt phẳng (P) là 3.
c) Tâm đường tròn (C) có tọa độ là H(1;3;1).
d) Phương trình mặt cầu (S) là \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 16\).
a) Từ diện tích đường tròn, tìm bán kính.
b) Áp dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
c) H là tâm đường tròn (C) nên H là hình chiếu của I lên mặt phẳng (P).
Lập phương trình đường thẳng IH, mà H thuộc (P) nên lập hệ phương trình tìm tọa độ điểm H.
d) Áp dụng định lí Pythagore tìm bán kính mặt cầu rồi lập phương trình mặt cầu.
a) Đúng. Đường tròn (C) có diện tích là \(25\pi \) nên bán kính là r = 5.
b) Đúng. \(d\left( {I;\left( P \right)} \right) = \frac{{\left| { - 1 - 2.2 + 2.\left( { - 1} \right) - 2} \right|}}{{\sqrt {1 + {{\left( { - 2} \right)}^2} + {2^2}} }} = 3\).
c) Sai. H là tâm đường tròn (C) nên H là hình chiếu của I lên mặt phẳng (P).
Phương trình đường thẳng IH là: \(\left\{ \begin{array}{l}x = - 1 + t\\y = 2 - 2t\\z = - 1 + 2t\end{array} \right.\).
Vì H thuộc IH và mặt phẳng (P) nên tọa độ điểm H là nghiệm của hệ:
\(\left\{ \begin{array}{l}x = - 1 + t\\y = 2 - 2t\\z = - 1 + 2t\\x - 2y + 2z - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 0\\z = 1\\t = 1\end{array} \right. \Rightarrow H\left( {0;0;1} \right)\).
d) Sai. Bán kính R của mặt cầu là \({R^2} = {r^2} + I{H^2} \Leftrightarrow R = \sqrt {{r^2} + I{H^2}} = \sqrt {{5^2} + {3^2}} = \sqrt {34} \).
Phương trình mặt cầu (S) tâm I(1;-2;1) bán kính \(R = \sqrt {34} \) là:
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 34\).
Lớp 11A1 có 45 học sinh, trong đó có 25 học sinh tham gia câu lạc bộ Tiếng Anh, 16 học sinh tham gia câu lạc bộ Nhảy, 12 học sinh vừa tham gia câu lạc bộ Tiếng Anh vừa tham gia câu lạc bộ Nhảy. Chọn ngẫu nhiên 1 học sinh. Xét các biến cố sau:
A: “Học sinh được chọn tham gia câu lạc bộ Tiếng Anh”.
B: “Học sinh được chọn tham gia câu lạc bộ Nhảy”.
a) \(P\left( A \right) = \frac{5}{{10}}\).
b) \(P\left( B \right) = \frac{7}{{20}}\).
c) \(P\left( {A|B} \right) = 0,75\).
d) Xác suất chọn được học sinh tham gia câu lạc bộ Nhảy, biết học sinh đó tham gia câu lạc bộ Tiếng Anh là 0,48.
a) \(P\left( A \right) = \frac{5}{{10}}\).
b) \(P\left( B \right) = \frac{7}{{20}}\).
c) \(P\left( {A|B} \right) = 0,75\).
d) Xác suất chọn được học sinh tham gia câu lạc bộ Nhảy, biết học sinh đó tham gia câu lạc bộ Tiếng Anh là 0,48.
Áp dụng công thức tính xác suất có điều kiện: \(P(A|B) = \frac{{P(A \cap B)}}{{P(B)}}\).
a)Sai. Có 25 trong tổng số 45 học sinh tham gia câu lạc bộ Tiếng Anh nên \(P(A) = \frac{{25}}{{45}} = \frac{5}{9}\).
b) Sai. Có 16 trong tổng số 45 học sinh tham gia câu lạc bộ Nhảy nên \(P(B) = \frac{{16}}{{45}}\).
c) Đúng. Xác suất chọn được học sinh tham gia cả hai câu lạc bộ là \(P(A \cap B) = \frac{{12}}{{45}} = \frac{4}{{15}}\).
Ta có \(P(A|B) = \frac{{P(A \cap B)}}{{P(B)}} = \frac{{\frac{4}{{15}}}}{{\frac{{16}}{{45}}}} = 0,75\).
d) Đúng. Ta có \(P(B|A) = \frac{{P(A \cap B)}}{{P(A)}} = \frac{{\frac{4}{{15}}}}{{\frac{5}{9}}} = 0,48\).
Một mảnh đất hình chữ nhật ABCD được quy hoạch như hình bên. Biết đường cong là đường hình sin của hàm số dạng y = asin(bx). Biết AB = \(2\pi \) (m) và AD = 4 (m). Phần tô đậm (giới hạn bởi đường cong và đoạn MN) được sử dụng để trồng hoa. Tính diện tích phần còn lại của mảnh vườn (đơn vị: \({m^2}\), làm tròn đến hàng phần chục).
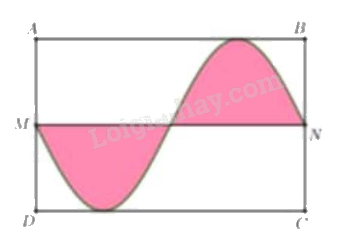
Quan sát biên độ và chu kì của đồ thị để tìm hệ số a, b. Áp dụng công thức tính diện tích hình phẳng bẳng tích phân.
Gắn trục tọa độ Oxy sao cho O là trung điểm của MN, đoạn thẳng ON nằm trên trục Ox.
Hàm số có biên độ là \(a = \frac{{AD}}{2} = \frac{4}{2} = 2\).
Hàm số có chu kì \(2\pi \) nên \(2\pi = \frac{{2\pi }}{{\left| b \right|}} \Rightarrow \left| b \right| = 1\).
Giả sử b = 1, ta có y = 2sinx. Với \(x = \frac{\pi }{2} \Rightarrow y = 2\sin \frac{\pi }{2} = 2\) (thõa mãn đồ thị).
Giả sử b = -1, ta có y = -2sinx. Với \(x = \frac{\pi }{2} \Rightarrow y = - 2\sin \frac{\pi }{2} = - 2\) (không thõa mãn đồ thị).
Do đó, hàm số y = asin(bx) đề bài cho là y = 2sinx.
Diện tích phần trồng hoa là:
\(\int\limits_{ - \pi }^\pi {\left| {2\sin x} \right|dx} = 2\int\limits_{ - \pi }^0 {( - \sin x)dx + 2} \int\limits_0^\pi {\sin xdx} = 8\) \(\left( {{m^2}} \right)\).
Diện tích hình chữ nhật ABCD là \(AB.AD = 2\pi .4 = 8\pi \) \(\left( {{m^2}} \right)\).
Diện tích phần còn lại của mảnh vườn là:
\(S = 8\pi - 8 \approx 17,1\) \(\left( {{m^2}} \right)\).
Chuồng I có 5 con gà mái, 2 con gà trống. Chuồng II có 3 con gà mái, 5 con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: “Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho 3 thì bác chọn chuồng I. Nếu số chấm không chia hết cho 3 thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà”. Tính xác suất để bác Mai bắt được con gà mái (kết quả làm tròn đến hàng phần trăm).
Áp dụng công thức xác suất toàn phần: \(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\bar A} \right).P\left( {B|\bar A} \right)\).
A: “Bắt được con gà mái”.
B: “Gà được bắt ở chuồng I”, \(\overline B \) là biến cố “Gà được bắt ở chuồng II”.
Nếu số chấm chia hết cho 3 (3 chấm hoặc 6 chấm) thì bác chọn chuồng I. Do đó, \(P\left( B \right) = \frac{2}{6} = \frac{1}{3}\).
Suy ra \(P\left( {\overline B } \right) = 1 - P\left( B \right) = 1 - \frac{1}{3} = \frac{2}{3}\).
Vì có 5 con gà mái trong tổng số 7 con gà ở chuồng I nên xác suất bắt được con gà mái nếu con gà đó ở chuồng I là:\(P\left( {A|B} \right) = \frac{5}{7}.\)
Vì có 3 con gà mái trong tổng số 8 con gà ở chuồng II nên xác suất bắt được con gà mái nếu con gà đó ở chuồng II là: \(P\left( {A|\overline B } \right) = \frac{3}{8}.\)
Theo công thức xác suất toàn phần ta có:
\(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right) = \frac{1}{3}.\frac{5}{7} + \frac{2}{3}.\frac{3}{8} = \frac{{41}}{{84}}. \approx 0,49\).
Một ô tô đang di chuyển với tốc độ 20 m/s thì hãm phanh nên tốc độ (m/s) của xe thay đổi theo thời gian t (giây) được tính theo công thức v(t) = 20 – 5t \((0 \le t \le 4)\). Kể từ lúc hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?
Tìm nghiệm \({t_0}\) của phương trình v(t) = 0 và tính \(s = \int\limits_0^{{t_0}} {v(t)} \).
Xe dừng khi \(v(t) = 0 \Leftrightarrow 20 - 5t = 0 \Leftrightarrow t = 4\).
Quãng đường xe di chuyển từ khi bắt đầu hãm phanh đến khi dừng hẳn là:
\(s = \int\limits_0^4 {v(t)} = \int\limits_0^4 {\left( {20 - 5t} \right)dt} = \left. {\left( {20t - \frac{5}{2}{t^2}} \right)} \right|_0^4 = 40\) (m).
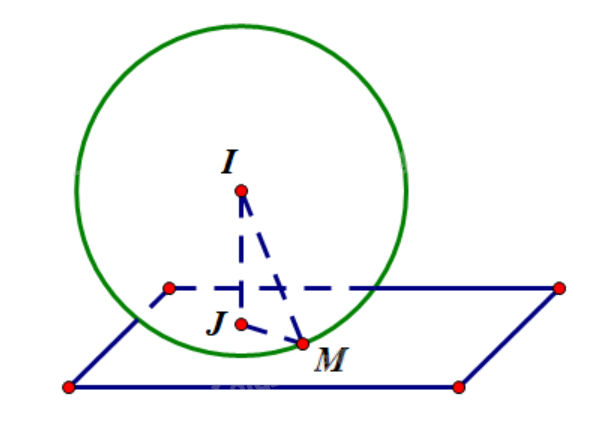
Công nghệ hỗ trợ trọng tài VAR (Video Assistant Referee) thiết lập một hệ tọa độ Oxyz để theo dõi vị trí của quả bóng M. Cho biết M đang nằm trên mặt sân có phương trình z = 0 đồng thời thuộc mặt cầu \((S):{\left( {x - 32} \right)^2} + {\left( {y - 50} \right)^2} + {\left( {z - 10} \right)^2} = 109\) (đơn vị độ dài tính theo mét). Gọi J là hình chiếu vuông góc của tâm I mặt cầu trên mặt sân. Khoảng cách từ vị trí M của quả bóng đến điểm J bằng bao nhiêu?
Tìm tọa độ của J. Tính \(JM = \sqrt {I{M^2} - I{J^2}} \) với IM bằng bán kính của mặt cầu (S).
Mặt cầu (S) có tâm I(32;50;10) và bán kính \(R = \sqrt {109} \).
Trong không gian Oxyz, mặt sân có phương trình z = 0 trùng với mặt phẳng (Oxy), suy ra hình chiếu vuông góc của I xuống mặt sân có tọa độ J(32;50;0).
Ta có \(IJ = \sqrt {{{(32 - 32)}^2} + {{(50 - 50)}^2} + {{(0 - 10)}^2}} = 10\).
Xét tam giác vuông IJM có IJ = 10, \(IM = R = \sqrt {109} \), suy ra \(JM = \sqrt {I{M^2} - I{J^2}} = \sqrt {109 - 100} = 3\).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {(x - 2)^2} - 1\), trục hoành và hai đường thẳng x = 1, x = 2 bằng bao nhiêu?
Áp dụng công thức tính diện tích hình phẳng \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \).
Xét dấu của biết thức \({(x - 2)^2} - 1\) để phá dấu trị tuyệt đối.
Ta có \({(x - 2)^2} - 1 = 0 \Leftrightarrow {(x - 2)^2} = 1 \Leftrightarrow \left[ \begin{array}{l}x - 2 = 1\\x - 1 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3 \notin [1;2]\\x = 0 \notin [1;2]\end{array} \right.\)
Trên đoạn [1;2] ta có \({(x - 2)^2} - 1 > 0\), suy ra \(\left| {{{(x - 2)}^2} - 1} \right| = {(x - 2)^2} - 1\).
Vậy diện tích hình phẳng cần tìm là \(S = \int\limits_1^2 {\left| {{{(x - 2)}^2} - 1} \right|dx} = \int\limits_1^2 {\left[ {{{(x - 2)}^2} - 1} \right]dx} = \frac{2}{3}\).
Trong không gian tọa độ (Oxyz), cho điểm M(1;2;-2) và mặt phẳng (P): 2x + y – 3z + 1 = 0. Phương trình của đường thẳng đi qua điểm M và vuông góc với (P) có phương trình tham số: \(\left\{ \begin{array}{l}x = 1 - 4t\\y = 2 + bt\\z = - 2 + ct\end{array} \right.\;\left( {t \in \mathbb{R}} \right)\). Khi đó giá trị của biểu thức \(P = {b^2} + {c^2}\) là bao nhiêu?
Do đường thẳng vuông góc với mặt phẳng (P) nên \(\overrightarrow u = \overrightarrow {{n_P}} \) là một vecto chỉ phương của đường thẳng cần tìm.
Theo đề bài phương trình tham số của đường thẳng \(\left\{ \begin{array}{l}x = 1 - 4t\\y = 2 + bt\\z = - 2 + ct\end{array} \right.\;\left( {t \in \mathbb{R}} \right)\) nên vecto chỉ phương của đường thẳng cần tìm có dạng \(\overrightarrow {u'} = \left( { - 4;b;c} \right)\).
Tìm b, c sao cho \(\overrightarrow u \) và \(\overrightarrow {u'} \) cùng phương.
Mặt phẳng (P): 2x + y – 3z + 1 = 0 có vecto pháp tuyến là \(\overrightarrow {{n_P}} = \left( {2;1; - 3} \right)\).
Do đường thẳng vuông góc với mặt phẳng (P) nên \(\overrightarrow u = \overrightarrow {{n_P}} = \left( {2;1; - 3} \right)\) là một vecto chỉ phương của đường thẳng cần tìm.
Theo đề bài phương trình tham số của đường thẳng \(\left\{ \begin{array}{l}x = 1 - 4t\\y = 2 + bt\\z = - 2 + ct\end{array} \right.\;\left( {t \in \mathbb{R}} \right)\) nên vecto chỉ phương của đường thẳng cần tìm có dạng \(\overrightarrow {u'} = \left( { - 4;b;c} \right)\) (2).
Vì \(\overrightarrow u \) và \(\overrightarrow {u'} \) đều là vecto chỉ phương của đường thẳng cần tìm nên chúng cùng phương với nhau.
Suy ra \(\frac{2}{{ - 4}} = \frac{1}{b} = \frac{{ - 3}}{c} \Leftrightarrow \left\{ \begin{array}{l}b = - 2\\c = 6\end{array} \right.\)
Vậy \(P = {b^2} + {c^2} = {( - 2)^2} + {6^2} = 40\).
Trong một khu du lịch, người ta cho du khách trải nghiệm thiên nhiên bằng cách đu theo đường trượt zipline từ vị trí A cao 15 m của tháp 1 này sang vị trí B cao 10 m của tháp 2 trong khung cảnh tuyệt đẹp xung quanh. Với hệ trục toạ độ Oxyz cho trước (đơn vị: mét), toạ độ của A và B lần lượt là (3; 2,5; 15) và (21; 27,5; 10). Xác định toạ độ của du khách khi ở độ cao 12 mét.

Lập phương trình tham số của đường thẳng d chứa đường trượt zipline. Cho z = 12, tìm t, sau đó thay t tìm x, y.
Đường thẳng d chứa đường trượt zipline đi qua điểm A(3; 2,5; 15) và có vecto chỉ phương là \(\overrightarrow {AB} = \left( {18;25; - 5} \right)\). Do đó, phương trình của d là: \(\left\{ \begin{array}{l}x = 3 + 18t\\y = 2,5 + 25t\\z = 15 - 5t\end{array} \right.\) \((t \in \mathbb{R})\).
Khi du khách khi ở độ cao 12 mét, ta có \(z = 12 \Leftrightarrow 15 - 5t = 12 \Leftrightarrow t = 0,6\).
Thay t vào phương trình đường thẳng, ta được tọa độ du khách là M(13,8; 17,5; 12).
Đề thi học kì 2 Toán 12 Chân trời sáng tạo - Đề số 2: Tổng quan và Hướng dẫn Ôn tập
Học kì 2 lớp 12 là giai đoạn quan trọng, quyết định kết quả học tập của học sinh. Việc chuẩn bị kỹ lưỡng cho kỳ thi học kì là vô cùng cần thiết. Đề thi học kì 2 Toán 12 Chân trời sáng tạo - Đề số 2 của tusach.vn được thiết kế để hỗ trợ tối đa quá trình ôn tập của bạn.
Cấu trúc Đề thi
Đề thi này bao gồm các dạng bài tập quen thuộc trong chương trình Toán 12 học kì 2, tập trung vào các chủ đề chính sau:
- Giải tích: Đạo hàm, tích phân, ứng dụng đạo hàm và tích phân.
- Hình học: Đường thẳng và mặt phẳng trong không gian, khối đa diện, khối tròn xoay.
- Số phức: Các phép toán trên số phức, phương trình bậc hai với hệ số thực.
- Xác suất và thống kê: Các khái niệm cơ bản về xác suất, biến ngẫu nhiên rời rạc.
Tại sao nên luyện tập với Đề số 2?
Có rất nhiều lý do để bạn lựa chọn Đề thi học kì 2 Toán 12 Chân trời sáng tạo - Đề số 2 để luyện tập:
- Bám sát chương trình: Đề thi được xây dựng dựa trên nội dung chương trình học chính thức của Bộ Giáo dục và Đào tạo.
- Đa dạng bài tập: Đề thi bao gồm nhiều dạng bài tập khác nhau, giúp bạn làm quen với các tình huống ra đề.
- Đáp án chi tiết: Đáp án đi kèm với đề thi được trình bày rõ ràng, dễ hiểu, giúp bạn tự đánh giá kết quả và rút kinh nghiệm.
- Miễn phí: Đề thi được cung cấp miễn phí trên tusach.vn.
Hướng dẫn ôn tập hiệu quả
Để đạt kết quả tốt nhất trong kỳ thi học kì 2, bạn nên kết hợp việc giải đề thi với việc ôn tập lý thuyết và thực hành các bài tập trong sách giáo khoa. Dưới đây là một số lời khuyên:
- Nắm vững kiến thức cơ bản: Đảm bảo bạn hiểu rõ các khái niệm, định lý và công thức quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
- Phân tích lỗi sai: Sau khi giải đề thi, hãy dành thời gian phân tích các lỗi sai và tìm cách khắc phục.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc bạn bè.
Tải Đề thi và Đáp án
Bạn có thể tải Đề thi học kì 2 Toán 12 Chân trời sáng tạo - Đề số 2 và đáp án chi tiết ngay tại tusach.vn. Chúc bạn ôn tập tốt và đạt kết quả cao trong kỳ thi!
Bảng so sánh các đề thi (ví dụ)
| Đề số | Chủ đề chính | Độ khó |
|---|---|---|
| Đề số 1 | Giải tích | Trung bình |
| Đề số 2 | Hình học | Khó |
| Đề số 3 | Số phức & Xác suất | Trung bình - Khó |
Tusach.vn luôn đồng hành cùng bạn trên con đường học tập. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu ôn thi hữu ích khác!