Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 2
Tổng quan nội dung
Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 2
Tusach.vn xin giới thiệu Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 2, được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo.
Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với dạng đề, rèn luyện kỹ năng giải quyết bài toán và tự đánh giá năng lực của bản thân trước kỳ thi quan trọng.
Đề bài
Cho hàm số f(x), bảng xét dấu của f’(x) như sau:

Hàm số f(x) nghịch biến trên khoảng nào dưới đây?
- A.
\((1; + \infty )\)
- B.
\(( - 1; + \infty )\)
- C.
\(( - \infty ;0)\)
- D.
\((0;1)\)
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ.
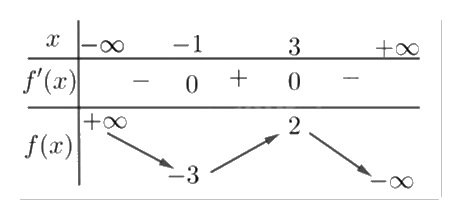
Điểm cực đại của hàm số đã cho là
- A.
\(x = 3\)
- B.
\(x = - 1\)
- C.
\(x = 2\)
- D.
\(x = - 3\)
Cho hàm số f(x) có đồ thị như hình dưới.
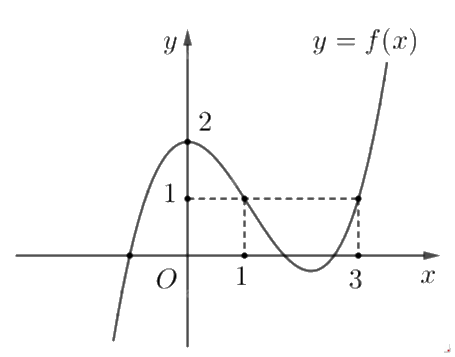
Giá trị lớn nhất của hàm số f(x) trên đoạn [0;3] là
- A.
1
- B.
2
- C.
3
- D.
0
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x + 3}}{{5x + 1}}\) là
- A.
\(y = 5\)
- B.
\(y = \frac{1}{5}\)
- C.
\(y = - \frac{1}{5}\)
- D.
\(y = 3\)
Cho hàm số \(f(x) = x - 3 + \frac{5}{{x - 2}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
- A.
y = x – 5
- B.
y = x – 2
- C.
y = x – 3
- D.
y = x + 2
Cho hàm số f(x) có đồ thị y = f’(x) như hình.
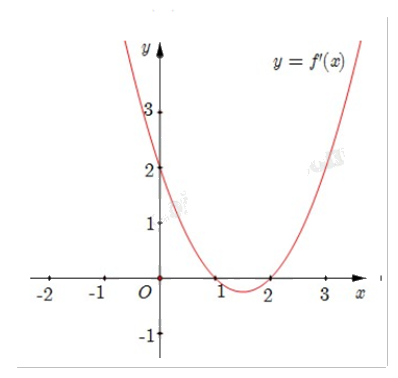
Hàm số f(x) có cực tiểu là
- A.
x = 2
- B.
x = 1
- C.
x = 0
- D.
Đáp án khác
Cho hình hộp ABCD.EFGH. Kết quả phép toán \(\overrightarrow {AB} - \overrightarrow {EH} \) là
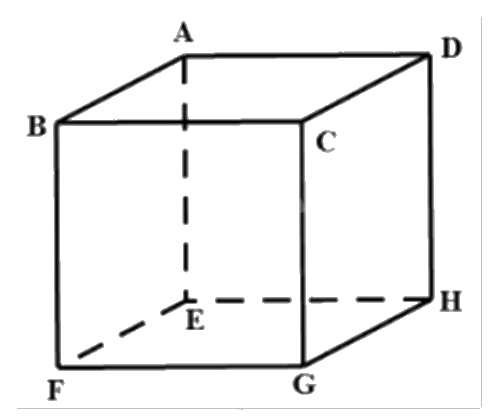
- A.
\(\overrightarrow {BD} \)
- B.
\(\overrightarrow {AE} \)
- C.
\(\overrightarrow {DB} \)
- D.
\(\overrightarrow {BH} \)
Cho biết G là trọng tâm tứ diện ABCD. Mệnh đề nào sau đây đúng?
- A.
\(GA = GB = GC = GD\)
- B.
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
- C.
\(\overrightarrow {GA} - \overrightarrow {GB} = \overrightarrow {GC} - \overrightarrow {GD} \)
- D.
\(GA + GB + GC + GD = 0\)
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-1;2) và B(4;-3;1). Tọa độ của vecto \(\overrightarrow {AB} \) là
- A.
(-3;2;1)
- B.
(3;-2;-1)
- C.
(5;-4;3)
- D.
(3;-4;-1)
Trong không gian với hệ trục tọa độ Oxyz, cho hai vecto \(\overrightarrow u = (3;0;1)\) và \(\overrightarrow v = (2;1;0)\). Tính tích vô hướng \(\overrightarrow u .\overrightarrow v \).
- A.
\(\overrightarrow u .\overrightarrow v = 8\)
- B.
\(\overrightarrow u .\overrightarrow v = 6\)
- C.
\(\overrightarrow u .\overrightarrow v = 0\)
- D.
\(\overrightarrow u .\overrightarrow v = - 6\)
Trong không gian Oxyz, gọi A’ là hình chiếu vuông góc của điểm A(2;3;4) lên mặt phẳng (Oxz). Tọa độ vecto \(\overrightarrow {AA'} \) là
- A.
(0;3;0)
- B.
(2;0;4)
- C.
(2;3;4)
- D.
(0;-3;0)
Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào.Kết quả khảo sát được ghi lai ở bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
- A.
4
- B.
20
- C.
9
- D.
108
Cho hàm số \(f(x) = {e^{{x^2} - 1}}\).
a) Hàm số đồng biến trên \(( - 1;1)\).
b) Hàm số nghịch biến trên khoảng (-3;-2).
c) Đồ thị hàm số có 1 tiệm cận.
d) Giao điểm của đồ thị và trục tung có tung độ là e.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Các cạnh bên SA = SB = SC = SD = 2a. Đặt \(\overrightarrow {SA} = \overrightarrow a \), \(\overrightarrow {SB} = \overrightarrow b \), \(\overrightarrow {SC} = \overrightarrow c \), \(\overrightarrow {SD} = \overrightarrow d \).
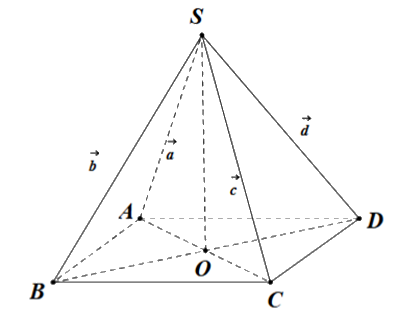
a) Các vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c ,\overrightarrow d \) có độ dài bằng nhau.
b) \(\overrightarrow {AC} \), \(\overrightarrow {BD} \) cùng phương.
c) Gọi O là giao điểm của AC và BD, khi đó \(\overrightarrow {SO} = \frac{1}{2}\left( {\overrightarrow b + \overrightarrow d } \right)\).
d) Độ dài của \(\overrightarrow b + \overrightarrow d \) bằng \(\frac{{a\sqrt {14} }}{2}\).
Trong không gian Oxyz, cho A(3;1;-2), B(-1;3;2), C(-6;3;6).
a) \(\overrightarrow {AB} = ( - 4;2;4)\).
b) Ba điểm A, B, C thẳng hàng.
c) Tọa độ trọng tâm của tam giác ABC là \(\left( { - \frac{4}{3};\frac{7}{3};2} \right)\).
d) Khi điểm E có tọa độ (8;1;2) thì ABCE là hình bình hành.
Nhiệt độ trong 55 ngày của một địa phương được cho trong bảng ghép lớp sau:

a) Giá trị đại diện của nhóm thứ hai theo chiều từ trái sang phải là 23,5.
b) Nhiệt độ trung bình của 55 ngày là 30 độ C.
c) Phương sai của mẫu số liệu trên bằng 19,44.
d) Độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần mười) là 4,5.
Một công ty sản xuất một sản phẩm. Bộ phận tài chính của công ty đưa ra hàm giá bán là p(x) = 1000 - 25x, trong đó p(x) (triệu đồng) là giá bán của mỗi sản phẩm mà tại giá bán này có x sản phẩm được bán ra. Doanh thu của công ty khi bán được 5 sản phẩm là bao nhiêu triệu đồng?
Đáp án:
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhận đầu tiên đến ngày thứ t là \(f(t) = 45{t^2} - {t^3}\), t = 0, 1, 2, …, 25. Nếu coi f là hàm số xác định trên [0;25] thì f’(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Xác định ngày mà tốc độ truyền bệnh là lớn nhất.
Đáp án:
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như sau:
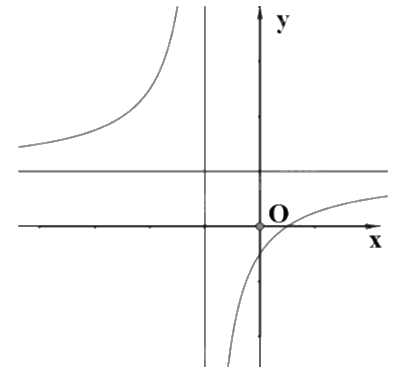
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
i) bd < 0.
ii) cd > 0.
iii) ac > 0.
iv) bc > 0.
v) ab < 0.
vi) ad < 0.
Đáp án:
Ba lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) cùng tác động vào một vật. Trong đó hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) tạo với nhau một góc \({110^o}\) và có độ lớn lần lượt là 9 N, 4 N. Lực \(\overrightarrow {{F_3}} \) vuông góc với các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) và có độ lớn 7 N. Độ lớn hợp lwujc của ba lực trên là bao nhiêu Newton (N)? Kết quả làm tròn đến hàng đơn vị.
Đáp án:
Hai chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Bắc 20 (km) và về phía Tây 10 (km), đồng thời cách mặt đất 0,7 (km). Chiếc máy bay thứ hai cách điểm xuất phát về phía Đông 30 (km) và về phía Nam 25 (km), đồng thời cách mặt đất 1 (km). Xác định khoảng cách giữa hai chiếc máy bay (km), làm tròn kết quả đến hàng đơn vị.

Đáp án:
Kết quả đo chiều cao của 200 cây keo 3 năm tuổi ở một nông trường được biểu diễn bằng số liệu ghép nhóm sau:

Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho (làm tròn kết quả đến chữ số thập phân thứ hai).
Đáp án:
Lời giải và đáp án
Cho hàm số f(x), bảng xét dấu của f’(x) như sau:

Hàm số f(x) nghịch biến trên khoảng nào dưới đây?
- A.
\((1; + \infty )\)
- B.
\(( - 1; + \infty )\)
- C.
\(( - \infty ;0)\)
- D.
\((0;1)\)
Đáp án : D
Quan sát bảng xét dấu và nhận xét.
Trên khoảng (0;1), f’(x) mang dấu âm nên f(x) nghịch biến trên (0;1).
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ.
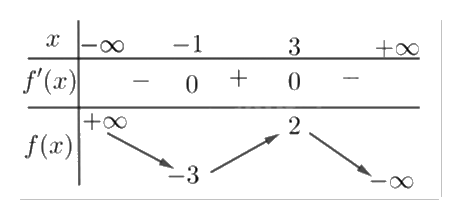
Điểm cực đại của hàm số đã cho là
- A.
\(x = 3\)
- B.
\(x = - 1\)
- C.
\(x = 2\)
- D.
\(x = - 3\)
Đáp án : A
Quan sát bảng biến thiên và nhận xét.
Hàm số đạt cực đại tại x = 3.
Cho hàm số f(x) có đồ thị như hình dưới.
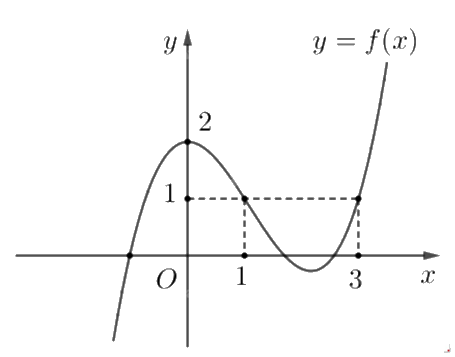
Giá trị lớn nhất của hàm số f(x) trên đoạn [0;3] là
- A.
1
- B.
2
- C.
3
- D.
0
Đáp án : B
Quan sát đồ thị và nhận xét.
Giá trị lớn nhất của f(x) trên đoạn [0;3] là y = 2 tại x = 0.
Tiệm cận ngang của đồ thị hàm số \(y = \frac{{x + 3}}{{5x + 1}}\) là
- A.
\(y = 5\)
- B.
\(y = \frac{1}{5}\)
- C.
\(y = - \frac{1}{5}\)
- D.
\(y = 3\)
Đáp án : B
Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to {\rm{\;}} + \infty } f(x) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to {\rm{\;}} - \infty } f(x) = {y_0}\).
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \frac{{x + 3}}{{5x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + \frac{3}{x}}}{{5 + \frac{1}{x}}} = \frac{1}{5}\) nên đồ thị hàm số f(x) có tiệm cận ngang là \(y = \frac{1}{5}\).
Cho hàm số \(f(x) = x - 3 + \frac{5}{{x - 2}}\). Tiệm cận xiên của đồ thị đã cho là đường thẳng
- A.
y = x – 5
- B.
y = x – 2
- C.
y = x – 3
- D.
y = x + 2
Đáp án : C
Đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (x - 3)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {x - 3 + \frac{5}{{x - 2}} - (x - 3)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{5}{{x - 2}} = 0\).
Vây y = x – 3 là tiệm cận xiên của đồ thị hàm số.
Cho hàm số f(x) có đồ thị y = f’(x) như hình.
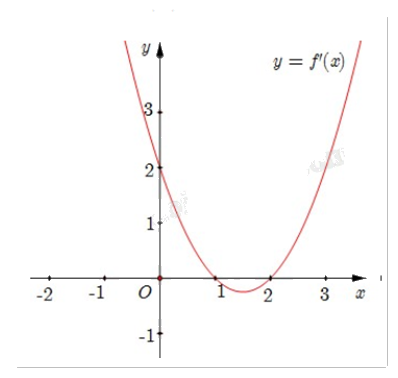
Hàm số f(x) có cực tiểu là
- A.
x = 2
- B.
x = 1
- C.
x = 0
- D.
Đáp án khác
Đáp án : A
Hàm số f(x) đạt cực tiểu tại \({x_0}\) khi \(f'({x_0}) = 0\) và f’(x) đổi dấu từ âm sang dương khi qua \({x_0}\).
Quan sát đồ thị y = f’(x) ta thấy f’(x) < 0 trên (1;2) và f’(x) > 0 trên \((2; + \infty )\) nên x = 2 là cực tiểu của hàm số f(x).
Cho hình hộp ABCD.EFGH. Kết quả phép toán \(\overrightarrow {AB} - \overrightarrow {EH} \) là
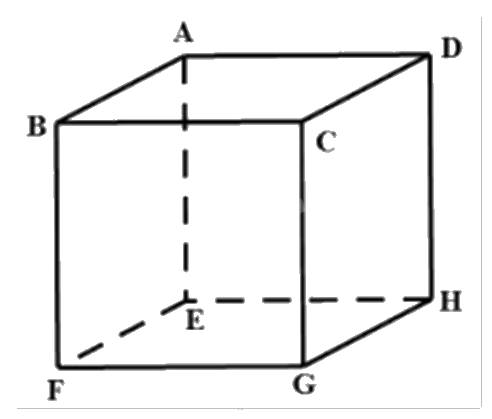
- A.
\(\overrightarrow {BD} \)
- B.
\(\overrightarrow {AE} \)
- C.
\(\overrightarrow {DB} \)
- D.
\(\overrightarrow {BH} \)
Đáp án : C
Dựa vào khái niệm vecto bằng nhau, vecto đối nhau, quy tắc ba điểm.
Ta có \(\overrightarrow {AB} - \overrightarrow {EH} = \overrightarrow {AB} + \overrightarrow {HE} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DA} + \overrightarrow {AB} = \overrightarrow {DB} \).
Cho biết G là trọng tâm tứ diện ABCD. Mệnh đề nào sau đây đúng?
- A.
\(GA = GB = GC = GD\)
- B.
\(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
- C.
\(\overrightarrow {GA} - \overrightarrow {GB} = \overrightarrow {GC} - \overrightarrow {GD} \)
- D.
\(GA + GB + GC + GD = 0\)
Đáp án : B
Sử dụng tính chất trọng tâm của tứ diện.
Vì G là trọng tâm của tứ diện ABCD nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-1;2) và B(4;-3;1). Tọa độ của vecto \(\overrightarrow {AB} \) là
- A.
(-3;2;1)
- B.
(3;-2;-1)
- C.
(5;-4;3)
- D.
(3;-4;-1)
Đáp án : B
\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\).
\(\overrightarrow {AB} = (4 - 1; - 3 + 1;1 - 2) = (3; - 2; - 1)\).
Trong không gian với hệ trục tọa độ Oxyz, cho hai vecto \(\overrightarrow u = (3;0;1)\) và \(\overrightarrow v = (2;1;0)\). Tính tích vô hướng \(\overrightarrow u .\overrightarrow v \).
- A.
\(\overrightarrow u .\overrightarrow v = 8\)
- B.
\(\overrightarrow u .\overrightarrow v = 6\)
- C.
\(\overrightarrow u .\overrightarrow v = 0\)
- D.
\(\overrightarrow u .\overrightarrow v = - 6\)
Đáp án : B
Sử dụng công thức tính tích vô hướng \(\overrightarrow a .\overrightarrow b = {x_a}.{x_b} + {y_a}.{y_b} + {z_a}.{z_b}\).
Ta có: \(\overrightarrow u .\overrightarrow v = 3.2 + 0.1 + 1.0 = 6\).
Trong không gian Oxyz, gọi A’ là hình chiếu vuông góc của điểm A(2;3;4) lên mặt phẳng (Oxz). Tọa độ vecto \(\overrightarrow {AA'} \) là
- A.
(0;3;0)
- B.
(2;0;4)
- C.
(2;3;4)
- D.
(0;-3;0)
Đáp án : D
Hình chiếu của điểm M(a;b;c) lên mặt phẳng (Oxz) là điểm M’(a;0;c).
Ta có A’(2;0;4) suy ra \(\overrightarrow {AA'} = (2 - 2;0 - 3;4 - 4) = (0; - 3;0)\).
Một công ty xây dựng khảo sát khách hàng xem họ có nhu cầu mua nhà ở mức giá nào.Kết quả khảo sát được ghi lai ở bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
- A.
4
- B.
20
- C.
9
- D.
108
Đáp án : B
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên chứa dữ liệu.
R = 30 – 10 = 20.
Cho hàm số \(f(x) = {e^{{x^2} - 1}}\).
a) Hàm số đồng biến trên \(( - 1;1)\).
b) Hàm số nghịch biến trên khoảng (-3;-2).
c) Đồ thị hàm số có 1 tiệm cận.
d) Giao điểm của đồ thị và trục tung có tung độ là e.
a) Hàm số đồng biến trên \(( - 1;1)\).
b) Hàm số nghịch biến trên khoảng (-3;-2).
c) Đồ thị hàm số có 1 tiệm cận.
d) Giao điểm của đồ thị và trục tung có tung độ là e.
Lập bảng biến thiên và nhận xét.
Tập xác định: D = R.
Ta có \(f'(x) = 2x.{e^{{x^2} - 1}} = 0 \Leftrightarrow x = 0\).
Bảng biến thiên:
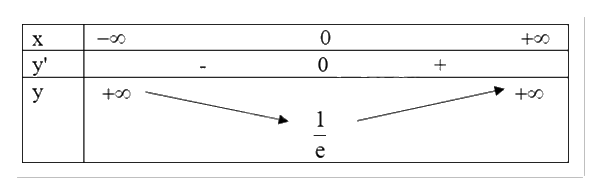
a) Sai. Hàm số nghịch biến trên (-1;0) và đồng biến trên (0;1).
b) Đúng. Hàm số nghịch biến trên (-3;-2).
c) Sai. Đồ thị hàm số không có tiệm cận.
d) Sai. Đồ thị cắt trục tung tại điểm có hoành độ bằng 0. Thay x = 0 vào hàm số ta được:
\(f(0) = {e^{{0^2} - 1}} = {e^{ - 1}} = \frac{1}{e}\).
Vậy đồ thị cắt trục tung tại điểm có tung độ là \(\frac{1}{e}\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Các cạnh bên SA = SB = SC = SD = 2a. Đặt \(\overrightarrow {SA} = \overrightarrow a \), \(\overrightarrow {SB} = \overrightarrow b \), \(\overrightarrow {SC} = \overrightarrow c \), \(\overrightarrow {SD} = \overrightarrow d \).
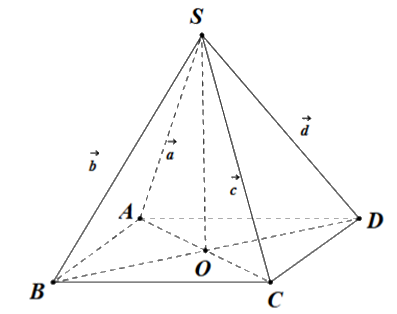
a) Các vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c ,\overrightarrow d \) có độ dài bằng nhau.
b) \(\overrightarrow {AC} \), \(\overrightarrow {BD} \) cùng phương.
c) Gọi O là giao điểm của AC và BD, khi đó \(\overrightarrow {SO} = \frac{1}{2}\left( {\overrightarrow b + \overrightarrow d } \right)\).
d) Độ dài của \(\overrightarrow b + \overrightarrow d \) bằng \(\frac{{a\sqrt {14} }}{2}\).
a) Các vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c ,\overrightarrow d \) có độ dài bằng nhau.
b) \(\overrightarrow {AC} \), \(\overrightarrow {BD} \) cùng phương.
c) Gọi O là giao điểm của AC và BD, khi đó \(\overrightarrow {SO} = \frac{1}{2}\left( {\overrightarrow b + \overrightarrow d } \right)\).
d) Độ dài của \(\overrightarrow b + \overrightarrow d \) bằng \(\frac{{a\sqrt {14} }}{2}\).
Dựa vào khái niệm vecto, vecto bằng nhau, cách tính độ dài vecto, tính chất trung điểm.
a) Đúng. Vì SA = SB = SC = SD = 2a nên các vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c ,\overrightarrow d \) đều có độ dài bằng 2a.
b) Sai. \(\overrightarrow {AC} \), \(\overrightarrow {BD} \) không cùng phương vì giá của chúng không song song với nhau.
c) Đúng. Vì O là giao hai đường chéo AC, BD của hình vuông ABCD nên O là trung điểm của AC, BD.
Khi đó \(2\overrightarrow {SO} = \overrightarrow {SB} + \overrightarrow {SD} \Leftrightarrow \overrightarrow {SO} = \frac{1}{2}\left( {\overrightarrow {SB} + \overrightarrow {SD} } \right) = \frac{1}{2}\left( {\overrightarrow b + \overrightarrow d } \right)\).
d) Sai. Từ câu c) ta có \(\overrightarrow b + \overrightarrow d = 2\overrightarrow {SO} \) suy ra \(\left| {\overrightarrow b + \overrightarrow d } \right| = 2\left| {\overrightarrow {SO} } \right| = 2.SO = 2\sqrt {S{A^2} - {{\left( {\frac{{AC}}{2}} \right)}^2}} = 2\sqrt {S{A^2} - {{\left( {\frac{{\sqrt 2 AB}}{2}} \right)}^2}} = 2\sqrt {{{(2a)}^2} - {{\left( {\frac{{\sqrt 2 a}}{2}} \right)}^2}} = a\sqrt {14} \).
Trong không gian Oxyz, cho A(3;1;-2), B(-1;3;2), C(-6;3;6).
a) \(\overrightarrow {AB} = ( - 4;2;4)\).
b) Ba điểm A, B, C thẳng hàng.
c) Tọa độ trọng tâm của tam giác ABC là \(\left( { - \frac{4}{3};\frac{7}{3};2} \right)\).
d) Khi điểm E có tọa độ (8;1;2) thì ABCE là hình bình hành.
a) \(\overrightarrow {AB} = ( - 4;2;4)\).
b) Ba điểm A, B, C thẳng hàng.
c) Tọa độ trọng tâm của tam giác ABC là \(\left( { - \frac{4}{3};\frac{7}{3};2} \right)\).
d) Khi điểm E có tọa độ (8;1;2) thì ABCE là hình bình hành.
Sử dụng các quy tắc cộng, trừ vecto, nhân vecto với một số, tích vô hướng của hai vecto.
a) Đúng. \(\overrightarrow {AB} = ( - 1 - 3;3 - 1;2 + 2) = ( - 4;2;4)\).
b) Sai. \(\overrightarrow {AC} = ( - 6 - 3;3 - 1;6 + 2) = ( - 9;2;8)\).
Ta có \(\frac{{ - 9}}{{ - 4}} \ne \frac{2}{2} \ne \frac{8}{4}\) nên \(\overrightarrow {AB} \), \(\overrightarrow {AC} \) không cùng phương. Vậy A, B, C không thẳng hàng.
c) Đúng. Gọi G là trọng tâm tam giác ABC. Ta có: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{3 - 1 - 6}}{3} = - \frac{4}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{1 + 3 + 3}}{3} = \frac{7}{3}\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{ - 2 + 2 + 6}}{3} = 2\end{array} \right.\).
Vậy G\(\left( { - \frac{4}{3};\frac{7}{3};2} \right)\).
d) Sai. ABCE là hình bình hành khi \(\overrightarrow {AB} = \overrightarrow {EC} \Leftrightarrow \left\{ \begin{array}{l} - 6 - {x_E} = - 4\\3 - {y_E} = 2\\6 - {z_E} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_E} = - 2\\{y_E} = 1\\{z_E} = 2\end{array} \right.\).
Vậy E(-2;1;2).
Nhiệt độ trong 55 ngày của một địa phương được cho trong bảng ghép lớp sau:

a) Giá trị đại diện của nhóm thứ hai theo chiều từ trái sang phải là 23,5.
b) Nhiệt độ trung bình của 55 ngày là 30 độ C.
c) Phương sai của mẫu số liệu trên bằng 19,44.
d) Độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần mười) là 4,5.
a) Giá trị đại diện của nhóm thứ hai theo chiều từ trái sang phải là 23,5.
b) Nhiệt độ trung bình của 55 ngày là 30 độ C.
c) Phương sai của mẫu số liệu trên bằng 19,44.
d) Độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần mười) là 4,5.
a) \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) với i = 1, 2,…, k là giá trị đại diện cho nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\).
b) Số trung bình: \(\bar x{\rm{\;}} = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\).
c) Phương sai: \({s^2} = \frac{{m{{({x_1} - \bar x)}^2} + ... + {m_k}{{({x_k} - \bar x)}^2}}}{n}\).
d) Độ lệch chuẩn: \(s = \sqrt {{s^2}} \).
a) Đúng. Giá trị đại diện của nhóm thứ hai là \(\frac{{22 + 25}}{2} = 23,5\).
b) Sai. Nhiệt độ trung bình của 55 ngày là:
\(\overline x = \frac{{5.20,5 + 7.23,5 + 8.26,5 + 16.29,5 + 12.32,5 + 7.35,5}}{{55}} = 28,9\) (độ C).
c) Đúng. Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{\begin{array}{l}5.{(20,5 - 28,9)^2} + 7.{(23,5 - 28,9)^2} + 8.{(26,5 - 28,9)^2}\\ + 16.{(29,5 - 28,9)^2} + 12.{(32,5 - 28,9)^2} + 7.{(35,5 - 28,9)^2}\end{array}}{{55}} = 19,44\).
d) Sai. Độ lệch chuẩn của mẫu số liệu trên là \(s = \sqrt {19,44} = 4,4\).
Một công ty sản xuất một sản phẩm. Bộ phận tài chính của công ty đưa ra hàm giá bán là p(x) = 1000 - 25x, trong đó p(x) (triệu đồng) là giá bán của mỗi sản phẩm mà tại giá bán này có x sản phẩm được bán ra. Doanh thu của công ty khi bán được 5 sản phẩm là bao nhiêu triệu đồng?
Đáp án:
Đáp án:
Thay x = 0,4 vào hàm số p(x) và tính kết quả.
Giá bán mỗi sản phẩm là p(x) = 1000 - 25x (triệu đồng).
Doanh thu khi bán được x sản phẩm là \(A\left( x \right) = x\left( {1000-25x} \right) = 1000x - 25{x^2}\) (triệu đồng).
Doanh thu khi bán được 5 sản phẩm là \(A\left( 5 \right) = 1000.5 - {25.5^2} = 4375\) (triệu đồng).
Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhận đầu tiên đến ngày thứ t là \(f(t) = 45{t^2} - {t^3}\), t = 0, 1, 2, …, 25. Nếu coi f là hàm số xác định trên [0;25] thì f’(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Xác định ngày mà tốc độ truyền bệnh là lớn nhất.
Đáp án:
Đáp án:
Tìm giá trị lớn nhất của f’(t) trên [0;25].
\(f'(t) = 90t - 3{t^2}\) là tốc độ truyền bệnh (người/ngày).
Ta có \(f''(t) = 90 - 6t = 0 \Leftrightarrow t = 15\).
Bảng biến thiên:
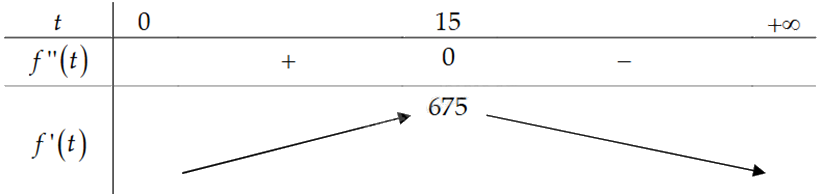
Từ bảng biến thiên, ta thấy tốc độ truyền bệnh lớn nhất là 675 người/ngày vào ngày thứ 15.
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như sau:
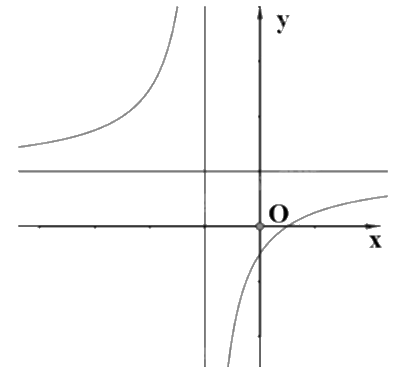
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
i) bd < 0.
ii) cd > 0.
iii) ac > 0.
iv) bc > 0.
v) ab < 0.
vi) ad < 0.
Đáp án:
Đáp án:
Xét dấu ac dựa vào tung độ của tiệm cận ngang.
Xét dấu cd dựa vào hoành độ của tiệm cận đứng.
Xét dấu bd dựa vào giao của đồ thị với trục tung.
Đồ thị cắt trục tung tại điểm có tung độ âm nên \(\frac{b}{d} < 0\) hay \(bd < 0\). Vậy i) đúng.
Tiệm cận đứng \(x = - \frac{d}{c}\) có hoành độ âm nên \(x = - \frac{d}{c} < 0\) hay \(cd > 0\). Vậy ii) đúng.
Tiệm cận ngang \(y = \frac{a}{c}\) có tung độ dương nên \(y = \frac{a}{c} > 0\) hay \(ac > 0\). Vậy iii) đúng.
Vì \(\left\{ \begin{array}{l}bd < 0\\cd > 0\end{array} \right.\) suy ra \(bc < 0\). Vậy iv) sai.
Vì \(\left\{ \begin{array}{l}bc < 0\\ac > 0\end{array} \right.\) suy ra \(ab < 0\). Vậy v) đúng.
Vì \(\left\{ \begin{array}{l}bd < 0\\ab < 0\end{array} \right.\) suy ra \(ad > 0\). Vậy vi) sai.
Vậy chỉ có iv) và vi) sai.
Ba lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) cùng tác động vào một vật. Trong đó hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) tạo với nhau một góc \({110^o}\) và có độ lớn lần lượt là 9 N, 4 N. Lực \(\overrightarrow {{F_3}} \) vuông góc với các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) và có độ lớn 7 N. Độ lớn hợp lwujc của ba lực trên là bao nhiêu Newton (N)? Kết quả làm tròn đến hàng đơn vị.
Đáp án:
Đáp án:
Sử dụng quy tắc tổng hợp lực.
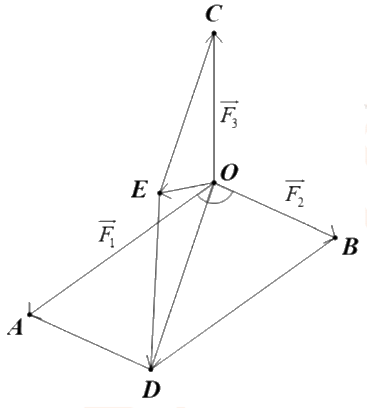
Giả sử các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) cùng tác động vào vật đặt tại điểm O.
Lấy các điểm A, B, C sao cho \(\overrightarrow {OA} = \overrightarrow {{F_1}} \), \(\overrightarrow {OB} = \overrightarrow {{F_2}} \), \(\overrightarrow {OC} = \overrightarrow {{F_3}} \).
Dựng các hình bình hành OADB và OCED như hình vẽ.
Hợp lực tác động vào vật là \(\overrightarrow F = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OD} + \overrightarrow {OC} = \overrightarrow {OE} \) (quy tắc hình bình hành).
Xét hình bình hành OADB:
\(O{D^2} = O{A^2} + O{B^2} + 2.OA.OB.\cos \widehat {AOB}\)
\( = {9^2} + {4^2} + 2.9.4.\cos {110^o} = 97 + 72\cos {110^o}\).
Vì \(\overrightarrow {{F_3}} \) vuông góc với các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) nên OC vuông góc với OA và OB.
Khi đó, OC vuông góc với mặt phẳng (OADB), suy ra OC vuông góc với OD.
Suy ra OCED là hình chữ nhật.
\(OE = \sqrt {O{C^2} + C{E^2}} = \sqrt {O{C^2} + O{D^2}} = \sqrt {{7^2} + {{\left( {97 + 72\cos {{110}^o}} \right)}^2}} \approx 11\).
Vậy độ lớn hợp lực \(\overrightarrow F = \overrightarrow {OE} \) bằng 11 N.
Hai chiếc máy bay không người lái cùng bay lên tại một địa điểm. Sau một thời gian bay, chiếc máy bay thứ nhất cách điểm xuất phát về phía Bắc 20 (km) và về phía Tây 10 (km), đồng thời cách mặt đất 0,7 (km). Chiếc máy bay thứ hai cách điểm xuất phát về phía Đông 30 (km) và về phía Nam 25 (km), đồng thời cách mặt đất 1 (km). Xác định khoảng cách giữa hai chiếc máy bay (km), làm tròn kết quả đến hàng đơn vị.

Đáp án:
Đáp án:
Chọn hệ trục tọa độ, tìm tọa độ hai chiếc máy bay dựa vào hệ trục đó rồi tính khoảng cách.
Công thức tính khoảng cách: \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
Chọn hệ trục tọa độ Oxyz, với góc đặt tại điểm xuất phát của hai chiếc máy bay, mặt phẳng (Oxy) trùng với mặt đất, trục Ox hướng về phía Bắc, trục Oy hướng về phía Tây, trục Oz hướng thẳng đứng lên trời, đơn vị đo lấy theo kilomet.
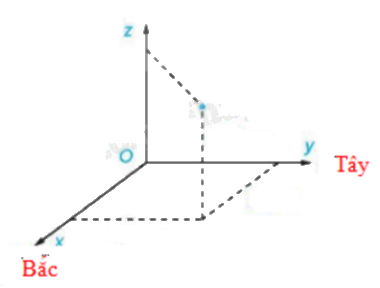
Chiếc máy bay thứ nhất có tọa độ (20; 10; 0,7).Chiếc máy bay thứ hai có tọa độ (-25; -30; 1).Do đó khoảng cách giữa hai chiếc máy bay là:
\(\sqrt {{{(20 + 25)}^2} + {{(10 + 30)}^2} + {{(0,7 - 1)}^2}} \approx 60\) (km).
Lưu ý: Đối với tính khoảng cách giữa hai điểm trong không gian, trong công thức ta có thể lấy tọa độ điểm đầu trừ điểm cuối hoặc tọa độ điểm cuối trừ điểm đầu (vì bình phương hiệu hai tọa độ là không đổi).
Kết quả đo chiều cao của 200 cây keo 3 năm tuổi ở một nông trường được biểu diễn bằng số liệu ghép nhóm sau:

Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho (làm tròn kết quả đến chữ số thập phân thứ hai).
Đáp án:
Đáp án:
Công thức: \({\Delta _Q} = {Q_3} - {Q_1}\).
Cỡ mẫu: n = 20 + 35 + 60 + 55 + 30 = 200.
Gọi \({x_1},{x_2},...,{x_{200}}\) là mẫu số liệu gốc được sắp xếp theo thứ tự không giảm.
Do \(\frac{n}{4} = 50\) nên tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{{{x_{50}} + {x_{51}}}}{2} \in [8,8;9,1)\).
\({Q_1} = 8,8 + \frac{{\frac{{200}}{4} - 20}}{{35}}(9,1 - 8,8) = \frac{{317}}{{35}}\).
Do \(\frac{{3n}}{4} = 150\) nên tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{{{x_{150}} + {x_{151}}}}{2} \in [9,4;9,7)\).
\({Q_3} = 9,4 + \frac{{\frac{{3.200}}{4} - (20 + 35 + 60)}}{{55}}(9,7 - 9,4) = \frac{{211}}{{22}}\).
Vậy \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{211}}{{22}} - \frac{{317}}{{35}} \approx 0,53\).
Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 2: Tổng quan và Hướng dẫn Ôn tập
Kỳ thi học kì 1 Toán 12 đóng vai trò quan trọng trong việc đánh giá quá trình học tập của học sinh trong nửa học kỳ đầu tiên. Đề thi Chân trời sáng tạo thường tập trung vào các chủ đề cốt lõi như Đại số, Giải tích, Hình học và các ứng dụng thực tế của Toán học.
Cấu trúc Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 2
Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 2 thường có cấu trúc tương tự như sau:
- Phần trắc nghiệm: Khoảng 20-30 câu, tập trung vào các kiến thức cơ bản, công thức và kỹ năng tính toán nhanh.
- Phần tự luận: Thường gồm 3-5 câu, yêu cầu học sinh trình bày chi tiết lời giải, áp dụng các kiến thức đã học để giải quyết các bài toán phức tạp hơn.
Nội dung chính của Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 2
Đề thi này bao gồm các nội dung chính sau:
- Đại số: Dãy số, cấp số cộng, cấp số nhân, giới hạn dãy số, đạo hàm.
- Giải tích: Nguyên hàm, tích phân, ứng dụng của đạo hàm để khảo sát hàm số.
- Hình học: Đường thẳng và mặt phẳng trong không gian, vectơ, quan hệ vuông góc, khoảng cách.
- Ứng dụng: Các bài toán thực tế liên quan đến các kiến thức đã học.
Làm thế nào để ôn thi hiệu quả cho Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 2?
Để đạt kết quả tốt nhất trong kỳ thi học kì 1 Toán 12, bạn nên:
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các công thức và định lý quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau, từ dễ đến khó, để rèn luyện kỹ năng giải quyết bài toán.
- Ôn tập theo cấu trúc đề thi: Làm quen với cấu trúc đề thi và phân bổ thời gian hợp lý cho từng phần.
- Sử dụng các tài liệu ôn tập: Tham khảo các đề thi tham khảo, đề thi năm trước và các tài liệu ôn tập khác.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, hãy hỏi thầy cô giáo, bạn bè hoặc tham gia các diễn đàn học tập trực tuyến.
Tusach.vn – Nguồn tài liệu ôn thi Toán 12 uy tín
Tusach.vn là một trong những website cung cấp tài liệu ôn thi Toán 12 uy tín và chất lượng nhất hiện nay. Chúng tôi cung cấp đầy đủ các loại tài liệu ôn tập, bao gồm:
- Đề thi học kì, đề thi thử
- Bài tập trắc nghiệm, bài tập tự luận
- Đáp án chi tiết, lời giải hay
- Các bài viết hướng dẫn ôn tập, bí quyết làm bài thi
Hãy truy cập tusach.vn ngay hôm nay để khám phá kho tài liệu ôn thi Toán 12 phong phú và hữu ích của chúng tôi!
Bảng so sánh các dạng bài tập thường gặp
| Dạng bài tập | Mức độ khó | Lời khuyên |
|---|---|---|
| Tính giới hạn | Dễ - Trung bình | Nắm vững các quy tắc tính giới hạn và các dạng giới hạn đặc biệt. |
| Giải phương trình, bất phương trình | Trung bình - Khó | Sử dụng các phương pháp giải phương trình, bất phương trình phù hợp. |
| Khảo sát hàm số | Khó | Nắm vững các bước khảo sát hàm số và các kỹ năng vẽ đồ thị hàm số. |
Chúc các bạn ôn thi tốt và đạt kết quả cao!