Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5
Tổng quan nội dung
Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5
Tusach.vn xin giới thiệu Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5, được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo.
Đề thi này là tài liệu ôn tập lý tưởng, giúp học sinh làm quen với các dạng bài tập thường gặp và rèn luyện kỹ năng giải đề. Đi kèm với đề thi là đáp án chi tiết, giúp học sinh tự đánh giá năng lực và tìm ra những điểm cần cải thiện.
Đề bài
Cho hàm số y = f(x) có bảng biến thiên sau:
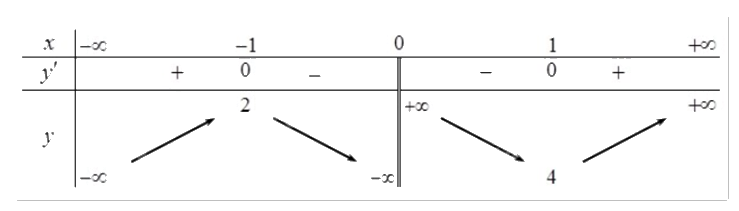
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
- A.
\(( - 1;1)\)
- B.
\((4; + \infty )\)
- C.
\(( - \infty ;2)\)
- D.
\((0;1)\)
Cho hàm số f(x) liên tục trên \(\mathbb{R}\) và có bảng xét dấu f’(x) như sau:

Số điểm cực đại của hàm số đã cho là
- A.
4
- B.
2
- C.
3
- D.
0
Cho hàm số f(x) có đồ thị như hình dưới.
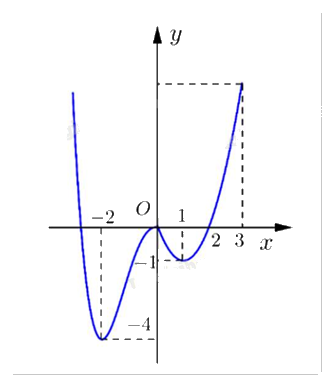
Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0;3] là
- A.
-1
- B.
1
- C.
2
- D.
3
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x - 3}}\) là
- A.
\(x = - 3\)
- B.
\(x = - 1\)
- C.
\(x = 1\)
- D.
\(x = 3\)
Đồ thị của hàm số \(y = 2x + 1 + \frac{2}{{3x - 1}}\) có đường tiệm cận xiên là
- A.
\(y = 3x - 1\)
- B.
\(y = 2 + x\)
- C.
\(y = 3 - x\)
- D.
\(y = 2x + 1\)
Cho hàm số f(x) có đạo hàm f’(x) xác định, liên tục trên \(\mathbb{R}\) và f’(x) có đồ thị như hình vẽ.
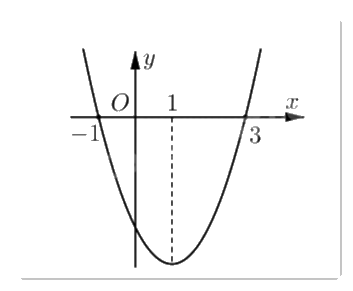
Khẳng định nào sau đây là đúng?
- A.
Hàm số đồng biến trên \((1; + \infty )\)
- B.
Hàm số đồng biến trên \(( - \infty ; - 1)\) và \((3; + \infty )\)
- C.
Hàm số nghịch biến trên \(( - \infty ;1)\)
- D.
Hàm số đồng biến trên \(( - 1;3)\)
Trong không gian cho 3 điểm M, N, P phân biệt. Tính \(\overrightarrow {PM} + \overrightarrow {MN} \).
- A.
\(\overrightarrow {NM} \)
- B.
\(\overrightarrow {MN} \)
- C.
\(\overrightarrow {NP} \)
- D.
\(\overrightarrow {PN} \)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(-1;2;5) và C(0;0;1). Trọng tâm G của tam giác ABC có tọa độ là
- A.
\((0;0;3)\)
- B.
\((0;0;9)\)
- C.
\(( - 1;0;3)\)
- D.
\((0;0;1)\)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-3;1), B(3;0;-2). Tính độ dài AB.
- A.
\(26\)
- B.
\(22\)
- C.
\(\sqrt {26} \)
- D.
\(\sqrt {22} \)
Cho hình lập phương ABCD.A’B’C’D’ có độ dài cạnh là a. Khi đó, \(\overrightarrow {AB} .\overrightarrow {AD} \) bằng
- A.
\({a^2}\)
- B.
\(0\)
- C.
\(a\)
- D.
\(\frac{{{a^2}}}{2}\)
Trong không gian Oxyz, cho điểm M(4;1;3). Điểm M’ đối xứng với M qua mặt phẳng (Oxz) có tọa độ
- A.
(-4;-1;3)
- B.
(-4;-1;-3)
- C.
(4;-1;3)
- D.
(4;1;-3)
Kết quả khảo sát cân nặng của một thùng táo ở một lô hàng cho trong bảng sau:

Khoảng biến thiên R của mẫu số liệu ghép nhóm trên là
- A.
\(R = 5\)
- B.
\(R = 24\)
- C.
\(R = 25\)
- D.
\(R = 10\)
Cho hàm số \(y = \frac{{ax + 1}}{{cx + d}}\) có đồ thị như hình vẽ:
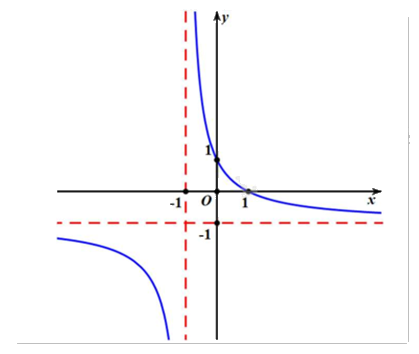
a) Hàm số luôn nghịch biến trên từng khoảng xác định.
b) \(\mathop {\lim }\limits_{x \to + \infty } y = - 1\).
c) \(\mathop {\lim }\limits_{x \to - {1^ + }} y = - \infty \).
d) Hệ số a = 2.
Cho hình hộp chữ nhật ABCD.EFGH có AB = AE = 2, AD = 3 và đặt \(\overrightarrow a = \overrightarrow {AB} \), \(\overrightarrow b = \overrightarrow {AD} \), \(\overrightarrow c = \overrightarrow {AE} \). Lấy điểm M thỏa mãn \(\overrightarrow {AM} = \frac{1}{5}\overrightarrow {AD} \) và điểm N thỏa mãn \(\overrightarrow {EN} = \frac{2}{5}\overrightarrow {EC} \).
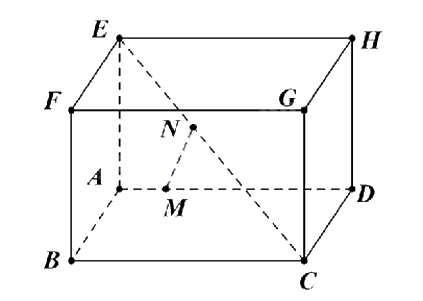
a) \(\overrightarrow {MA} = - \frac{1}{5}\overrightarrow b \).
b) \(\overrightarrow {EN} = \frac{2}{5}\left( {\overrightarrow a - \overrightarrow b + \overrightarrow c } \right)\).
c) \(\left( {m.\overrightarrow a + n.\overrightarrow b + p.\overrightarrow c } \right) = {m^2}.{\overrightarrow a ^2} + {n^2}.{\overrightarrow b ^2} + {p^2}.{\overrightarrow c ^2}\) với m, n, p là các số thực
d) \(MN = \frac{{\sqrt {61} }}{5}\).
Trong không gian Oxyz, cho các điểm A(2;-3;3), B(-2;1;2), C(3;-1;2).
a) \(\overrightarrow {AB} = ( - 3;3;1)\).
b) \(\overrightarrow {AB} = 3\overrightarrow {AC} \).
c) Ba điểm A, B, C không thẳng hàng.
d) Tọa độ chân đương cao vẽ từ A của tam giác ABC là \(\left( { - \frac{{47}}{{29}};\frac{{13}}{{29}};2} \right)\).
Thời gian chạy tập luyện cự li 100 mét của một vận đồng viên được cho trong bảng sau:

a) Số lần chạy từ 12 giây trở lên là 1.
b) Thời gian chạy trung bình của vận động viên là 10,9 giây.
c) Phương sai của mẫu số liệu trên bằng 0,168.
d) Độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần mười) là 0,5.
Một vât được phóng thẳng đứng lên trên từ mặt đất với tốc độ ban đầu là 32,5 m/s (bỏ qua sức cản của không khí), độ cao (tính bằng mét) của vật sau t giây được cho bởi công thức \(h(t) = 32,5t - 4,9{t^2}\). Vận tốc của vật sau 3 giây bằng bao nhiêu m/s?
Đáp án:
Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao là h (cm) và thể tích là 4000 \(c{m^3}\). Tìm độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.
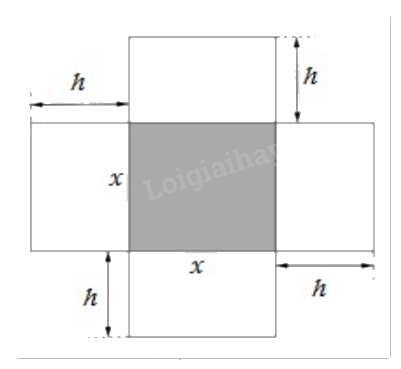
Đáp án:
Trong Vật lý, ta biết rằng khi mắc song song hai điện trở \({R_1}\) và \({R_2}\), thì điện trở tương đương R của mạch điện được tính theo công thức \(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) (theo Vật lý đại cương, NXB Giáo dục Việt Nam, 2016). Giả sử một điện trở \(10\Omega \) được mắc song song với một biến trở x thì điện trở tương đường R là hàm số \(\)\(y = \frac{{10x}}{{10 + x}}\) với x > 0. Điện trở tương đương của mạch không thể vượt quá bao nhiêu?
Đáp án:
Một chiếc cân đòn tay đang cân một vật có khối lượng m = 3 kg được thiết kế với đĩa cân được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có \(\widehat {ASC} = {90^o}\). Biết độ lớn của lực căng cho mỗi sợi xích có dạng \(\frac{{a\sqrt 2 }}{4}\). Lấy g = 10 \(m/{s^2}\), khi đó giá trị của a bằng bao nhiêu?
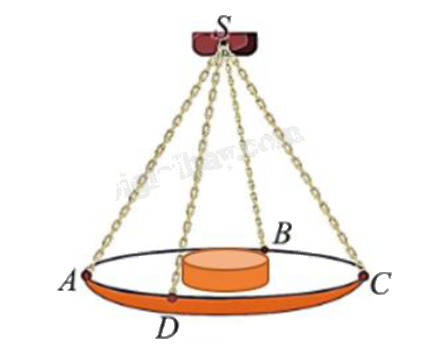
Đáp án:
Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất nằm cách điểm xuất phát 2,5 km về phía nam và 2 km về phía đông, đồng thời cách mặt đất 0,8 km. Chiếc thứ hai nằm cách điểm xuất phát 1,5 km về phía bắc và 3 km về phía tây, đồng thời cách mặt đất 0,6 km. Người ta cần tìm một vị trí trên mặt đất để tiếp nhiên liệu cho hai khinh khí cầu sao cho tổng khoảng cách từ vị trí đó tới hai khinh khí cầu nhỏ nhất. Giả sử vị trí cần tìm cách địa điểm hai khinh khí cầu bay lên là a km theo hướng nam và b km theo hướng tây. Tính tổng 2a + 3b.
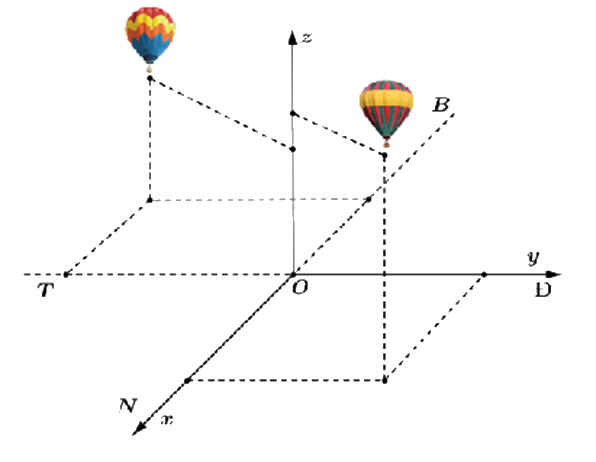
Đáp án:
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Tính khoảng tứ phân vị của mẫu số liệu.
Đáp án:
Lời giải và đáp án
Cho hàm số y = f(x) có bảng biến thiên sau:
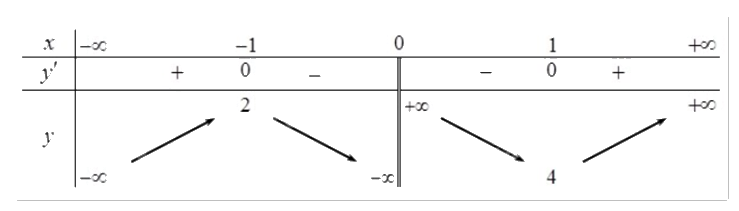
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
- A.
\(( - 1;1)\)
- B.
\((4; + \infty )\)
- C.
\(( - \infty ;2)\)
- D.
\((0;1)\)
Đáp án : D
Quan sát bảng biến thiên và nhận xét.
Trên khoảng (0;1), f’(x) mang dấu âm nên f(x) nghịch biến trên (0;1).
Cho hàm số f(x) liên tục trên \(\mathbb{R}\) và có bảng xét dấu f’(x) như sau:

Số điểm cực đại của hàm số đã cho là
- A.
4
- B.
2
- C.
3
- D.
0
Đáp án : B
Hàm số đạt cực đại tại điểm \({x_0}\) khi \(f'({x_0}) = 0\) hoặc \(f'({x_0})\) không xác định và qua \({x_0}\) thì f’(x) đổi dấu từ dương sang âm.
Tập xác định: \(D = \mathbb{R}\).
Quan sát bảng xét dấu, thấy:
+ \(f'(x) > 0\) khi \(x \in ( - \infty ; - 1)\) và \(f'(x) < 0\) khi \(x \in ( - 1;0)\); \(f'( - 1) = 0\).
+ \(f'(x) > 0\) khi \(x \in (0;1)\) và \(f'(x) < 0\) khi \(x \in (1;2)\); \(f'(1)\) không tồn tại.
Vậy hàm số có hai điểm cực đại là x = -1, x = 1.
Cho hàm số f(x) có đồ thị như hình dưới.
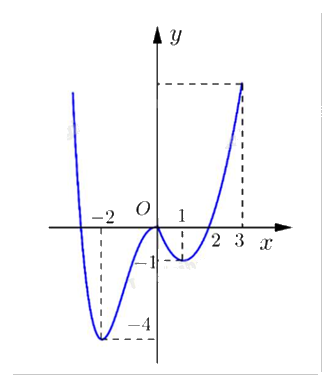
Giá trị nhỏ nhất của hàm số f(x) trên đoạn [0;3] là
- A.
-1
- B.
1
- C.
2
- D.
3
Đáp án : A
Quan sát đồ thị và nhận xét.
Giá trị nhỏ nhất của f(x) trên đoạn [0;3] là y = -1 tại x = 1.
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x - 3}}\) là
- A.
\(x = - 3\)
- B.
\(x = - 1\)
- C.
\(x = 1\)
- D.
\(x = 3\)
Đáp án : D
Đường thẳng \(x = {x_0}\) gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = {\rm{\;}} + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = {\rm{\;}} - \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = {\rm{\;}} + \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = {\rm{\;}} - \infty \).
Ta có: \(\mathop {\lim }\limits_{x \to {3^ + }} (x + 1) = 3 + 1 = 4\); \(\mathop {\lim }\limits_{x \to {3^ + }} (x - 3) = 3 - 3 = 0\) và x – 3 > 0.
Suy ra \(\mathop {\lim }\limits_{x \to {3^ + }} y = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{x - 1}}{{x - 3}} = + \infty \).
Vậy đồ thị hàm số \(y = \frac{{x - 1}}{{x - 3}}\) có tiệm cận đứng là x = 3.
Đồ thị của hàm số \(y = 2x + 1 + \frac{2}{{3x - 1}}\) có đường tiệm cận xiên là
- A.
\(y = 3x - 1\)
- B.
\(y = 2 + x\)
- C.
\(y = 3 - x\)
- D.
\(y = 2x + 1\)
Đáp án : D
Đường thẳng y = ax + b là tiệm cận xiên của đồ thị hàm số f(x) nếu \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (ax + b)} \right] = 0\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } \left[ {f(x) - (ax + b)} \right] = 0\).
Ta có \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f(x) - (2x + 1)} \right] = \mathop {\lim }\limits_{x \to + \infty } \left[ {2x + 1 + \frac{2}{{3x - 1}} - (2x + 1)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{{3x - 1}} = 0\).
Vây y = 2x + 1 là tiệm cận xiên của đồ thị hàm số.
Cho hàm số f(x) có đạo hàm f’(x) xác định, liên tục trên \(\mathbb{R}\) và f’(x) có đồ thị như hình vẽ.
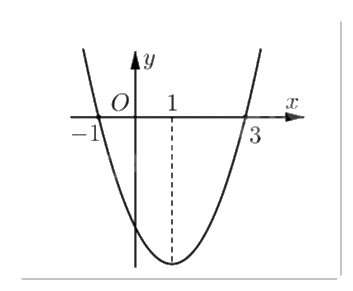
Khẳng định nào sau đây là đúng?
- A.
Hàm số đồng biến trên \((1; + \infty )\)
- B.
Hàm số đồng biến trên \(( - \infty ; - 1)\) và \((3; + \infty )\)
- C.
Hàm số nghịch biến trên \(( - \infty ;1)\)
- D.
Hàm số đồng biến trên \(( - 1;3)\)
Đáp án : B
Hàm số f(x) đồng biến khi f’(x) > 0 (phần đồ thị f’(x) nằm phía trên trục hoành).
Quan sát đồ thị y = f’(x) ta thấy f’(x) > 0 trên \(( - \infty ; - 1)\) và \((3; + \infty )\) nên f(x) đồng biến trên hai khoảng trên.
Trong không gian cho 3 điểm M, N, P phân biệt. Tính \(\overrightarrow {PM} + \overrightarrow {MN} \).
- A.
\(\overrightarrow {NM} \)
- B.
\(\overrightarrow {MN} \)
- C.
\(\overrightarrow {NP} \)
- D.
\(\overrightarrow {PN} \)
Đáp án : D
Dựa vào quy tắc ba điểm.
Ta có \(\overrightarrow {PM} + \overrightarrow {MN} = \overrightarrow {PN} \).
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(-1;2;5) và C(0;0;1). Trọng tâm G của tam giác ABC có tọa độ là
- A.
\((0;0;3)\)
- B.
\((0;0;9)\)
- C.
\(( - 1;0;3)\)
- D.
\((0;0;1)\)
Đáp án : A
Sử dụng công thức tính tọa độ trọng tâm.
Ta có \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 - 1 + 0}}{3} = 0\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{ - 2 + 2 + 0}}{3} = 0\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{3 + 5 + 1}}{3} = 3\end{array} \right.\) suy ra G(0;0;3).
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;-3;1), B(3;0;-2). Tính độ dài AB.
- A.
\(26\)
- B.
\(22\)
- C.
\(\sqrt {26} \)
- D.
\(\sqrt {22} \)
Đáp án : D
Công thức tính độ dài vecto: \(\left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} \).
\(\left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2} + {{\left( {{z_B} - {z_A}} \right)}^2}} = \sqrt {{{(3 - 1)}^2} + {{(0 + 3)}^2} + {{( - 2 - 1)}^2}} = \sqrt {22} \).
Cho hình lập phương ABCD.A’B’C’D’ có độ dài cạnh là a. Khi đó, \(\overrightarrow {AB} .\overrightarrow {AD} \) bằng
- A.
\({a^2}\)
- B.
\(0\)
- C.
\(a\)
- D.
\(\frac{{{a^2}}}{2}\)
Đáp án : B
Sử dụng quy tắc tính tích vô hướng của hai vecto.
Vì ABCD.A’B’C’D’ là hình lập phương nên AB vuông góc với AD.
Khi đó \(\overrightarrow {AB} .\overrightarrow {AD} = 0\).
Trong không gian Oxyz, cho điểm M(4;1;3). Điểm M’ đối xứng với M qua mặt phẳng (Oxz) có tọa độ
- A.
(-4;-1;3)
- B.
(-4;-1;-3)
- C.
(4;-1;3)
- D.
(4;1;-3)
Đáp án : C
Điểm M’ đối xứng với M(a;b;c) qua mặt phẳng (Oxz) có tọa độ M’(a;-b;c).
Điểm M’ đối xứng với M(4;1;3) qua mặt phẳng (Oxz) có tọa độ M’(4;-1;3).
Kết quả khảo sát cân nặng của một thùng táo ở một lô hàng cho trong bảng sau:

Khoảng biến thiên R của mẫu số liệu ghép nhóm trên là
- A.
\(R = 5\)
- B.
\(R = 24\)
- C.
\(R = 25\)
- D.
\(R = 10\)
Đáp án : C
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên chứa dữ liệu.
R = 175 – 150 = 25.
Cho hàm số \(y = \frac{{ax + 1}}{{cx + d}}\) có đồ thị như hình vẽ:
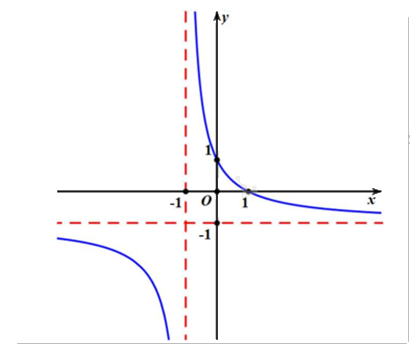
a) Hàm số luôn nghịch biến trên từng khoảng xác định.
b) \(\mathop {\lim }\limits_{x \to + \infty } y = - 1\).
c) \(\mathop {\lim }\limits_{x \to - {1^ + }} y = - \infty \).
d) Hệ số a = 2.
a) Hàm số luôn nghịch biến trên từng khoảng xác định.
b) \(\mathop {\lim }\limits_{x \to + \infty } y = - 1\).
c) \(\mathop {\lim }\limits_{x \to - {1^ + }} y = - \infty \).
d) Hệ số a = 2.
Quan sát đồ thị và nhận xét.
a) Đúng. Đồ thị hàm số đi xuống từ trái sang trên từng khoảng xác định.
b) Đúng. \(\mathop {\lim }\limits_{x \to + \infty } y = - 1\).
c) Sai. \(\mathop {\lim }\limits_{x \to - {1^ + }} y = + \infty \).
d) Sai. Vì đồ thị đi qua điểm (0;1) nên \(1 = \frac{{a.0 + 1}}{{c.0 + d}} \Leftrightarrow d = 1\).
Đồ thị có tiệm cận đứng là đường thẳng x = -1 nên \( - \frac{d}{c} = - 1 \Leftrightarrow - \frac{1}{c} = - 1 \Leftrightarrow c = 1\).
Đồ thị có tiệm cận ngang là đường thẳng y = -1 nên \(\frac{a}{c} = - 1 \Leftrightarrow \frac{a}{1} = - 1 \Leftrightarrow a = - 1\).
Vậy hệ số a = -1.
Cho hình hộp chữ nhật ABCD.EFGH có AB = AE = 2, AD = 3 và đặt \(\overrightarrow a = \overrightarrow {AB} \), \(\overrightarrow b = \overrightarrow {AD} \), \(\overrightarrow c = \overrightarrow {AE} \). Lấy điểm M thỏa mãn \(\overrightarrow {AM} = \frac{1}{5}\overrightarrow {AD} \) và điểm N thỏa mãn \(\overrightarrow {EN} = \frac{2}{5}\overrightarrow {EC} \).
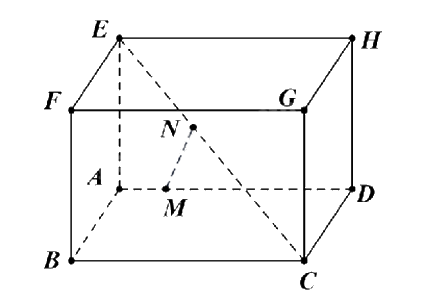
a) \(\overrightarrow {MA} = - \frac{1}{5}\overrightarrow b \).
b) \(\overrightarrow {EN} = \frac{2}{5}\left( {\overrightarrow a - \overrightarrow b + \overrightarrow c } \right)\).
c) \(\left( {m.\overrightarrow a + n.\overrightarrow b + p.\overrightarrow c } \right) = {m^2}.{\overrightarrow a ^2} + {n^2}.{\overrightarrow b ^2} + {p^2}.{\overrightarrow c ^2}\) với m, n, p là các số thực
d) \(MN = \frac{{\sqrt {61} }}{5}\).
a) \(\overrightarrow {MA} = - \frac{1}{5}\overrightarrow b \).
b) \(\overrightarrow {EN} = \frac{2}{5}\left( {\overrightarrow a - \overrightarrow b + \overrightarrow c } \right)\).
c) \(\left( {m.\overrightarrow a + n.\overrightarrow b + p.\overrightarrow c } \right) = {m^2}.{\overrightarrow a ^2} + {n^2}.{\overrightarrow b ^2} + {p^2}.{\overrightarrow c ^2}\) với m, n, p là các số thực
d) \(MN = \frac{{\sqrt {61} }}{5}\).
Dựa vào khái niệm vecto cùng phương, cùng hướng, cách xác định độ dài vecto, quy tắc cộng, trừ, nhân vecto với một số, quy tắc hình hộp.
a) Đúng. Ta có \(\overrightarrow {MA} = - \overrightarrow {AM} = - \frac{1}{5}\overrightarrow {AD} = - \frac{1}{5}\overrightarrow b \).
b) Sai. \(\overrightarrow {EN} = \frac{2}{5}\overrightarrow {EC} = \frac{2}{5}\left( {\overrightarrow {EF} + \overrightarrow {EH} + \overrightarrow {EA} } \right) = \frac{2}{5}\left( {\overrightarrow a - \overrightarrow b + \overrightarrow c } \right)\).
c) Đúng. \(\left( {m.\overrightarrow a + n.\overrightarrow b + p.\overrightarrow c } \right) = {m^2}.{\overrightarrow a ^2} + {n^2}.{\overrightarrow b ^2} + {p^2}.{\overrightarrow c ^2} + 2mn\overrightarrow a .\overrightarrow b + 2np\overrightarrow b .\overrightarrow c + 2mp\overrightarrow a .\overrightarrow c = {m^2}.{\overrightarrow a ^2} + {n^2}.{\overrightarrow b ^2} + {p^2}.{\overrightarrow c ^2}\)
(vì \(\overrightarrow a \), \(\overrightarrow b \), \(\overrightarrow c \) đôi một vuông góc nên \(\overrightarrow a .\overrightarrow b = \overrightarrow b .\overrightarrow c = \overrightarrow b .\overrightarrow c = 0\)).
d) Đúng. \(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AE} + \overrightarrow {EN} = - \frac{1}{5}\overrightarrow b + \overrightarrow c + \frac{2}{5}\left( {\overrightarrow a + \overrightarrow b - \overrightarrow c } \right) = \frac{2}{5}\overrightarrow a + \frac{1}{5}\overrightarrow b + \frac{3}{5}\overrightarrow c \).
\(M{N^2} = {\left( {\overrightarrow {MN} } \right)^2} = {\left( {\frac{2}{5}\overrightarrow a + \frac{1}{5}\overrightarrow b + \frac{3}{5}\overrightarrow c } \right)^2} = \frac{4}{{25}}{\overrightarrow a ^2} + \frac{1}{{25}}{\overrightarrow b ^2} + \frac{9}{{25}}{\overrightarrow c ^2} = \frac{4}{{25}}.4 + \frac{1}{{25}}.9 + \frac{9}{{25}}.4 = \frac{{61}}{{25}}\).
Suy ra \(MN = \frac{{\sqrt {61} }}{5}\).
Trong không gian Oxyz, cho các điểm A(2;-3;3), B(-2;1;2), C(3;-1;2).
a) \(\overrightarrow {AB} = ( - 3;3;1)\).
b) \(\overrightarrow {AB} = 3\overrightarrow {AC} \).
c) Ba điểm A, B, C không thẳng hàng.
d) Tọa độ chân đương cao vẽ từ A của tam giác ABC là \(\left( { - \frac{{47}}{{29}};\frac{{13}}{{29}};2} \right)\).
a) \(\overrightarrow {AB} = ( - 3;3;1)\).
b) \(\overrightarrow {AB} = 3\overrightarrow {AC} \).
c) Ba điểm A, B, C không thẳng hàng.
d) Tọa độ chân đương cao vẽ từ A của tam giác ABC là \(\left( { - \frac{{47}}{{29}};\frac{{13}}{{29}};2} \right)\).
Sử dụng các quy tắc cộng, trừ vecto, nhân vecto với một số, tích vô hướng của hai vecto.
a) Sai. \(\overrightarrow {AB} = ( - 2 - 1;1 + 2;2 - 3) = ( - 3;3; - 1)\).
b) Sai. \(\overrightarrow {AC} = (3 - 1; - 1 + 2;2 - 3) = (2;1; - 1)\), suy ra \(3\overrightarrow {AC} = (6;3; - 3) \ne \overrightarrow {AB} \).
c) Đúng. Ta thấy \(\frac{{ - 3}}{2} \ne \frac{3}{1} \ne \frac{{ - 1}}{{ - 1}}\) suy ra \(\overrightarrow {AB} \), \(\overrightarrow {AC} \) không cùng phương. Vậy A, B, C không thẳng hàng.
d) Sai. Gọi A’(x;y;z) là chân đường cao hạ từ A của tam giác ABC.
Khi đó \(\overrightarrow {AA'} .\overrightarrow {BC} = 0\) (1) và \(\overrightarrow {BC} \), \(\overrightarrow {BA'} \) cùng phương (2).
Ta có \(\overrightarrow {AA'} = (x - 1;y + 2;z - 3)\), \(\overrightarrow {BC} = (3 + 2; - 1 - 1;2 - 2) = (5; - 2;0)\), \(\overrightarrow {BA'} = (x + 2;y - 1;z - 2)\).
(1) \( \Leftrightarrow 5(x - 1) - 2(y + 2) + 0(z - 3) = 0 \Leftrightarrow 5x - 2y = 9\).
(2) \( \Leftrightarrow \left\{ \begin{array}{l}\frac{{x + 2}}{5} = \frac{{y - 1}}{{ - 2}}\\z - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 5y = 1\\z = 2\end{array} \right.\)
Từ (1) và (2) suy ra \(\left\{ \begin{array}{l}x = \frac{{47}}{{29}}\\y = - \frac{{13}}{{29}}\\z = 2\end{array} \right.\), hay \(A'\left( {\frac{{47}}{{29}}; - \frac{{13}}{{29}};2} \right)\).
Thời gian chạy tập luyện cự li 100 mét của một vận đồng viên được cho trong bảng sau:

a) Số lần chạy từ 12 giây trở lên là 1.
b) Thời gian chạy trung bình của vận động viên là 10,9 giây.
c) Phương sai của mẫu số liệu trên bằng 0,168.
d) Độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần mười) là 0,5.
a) Số lần chạy từ 12 giây trở lên là 1.
b) Thời gian chạy trung bình của vận động viên là 10,9 giây.
c) Phương sai của mẫu số liệu trên bằng 0,168.
d) Độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần mười) là 0,5.
a) Quan sát tần số trong bảng số liệu.
b) Số trung bình: \(\bar x{\rm{\;}} = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\).
c) Phương sai: \({s^2} = \frac{{m{{({x_1} - \bar x)}^2} + ... + {m_k}{{({x_k} - \bar x)}^2}}}{n}\).
d) Độ lệch chuẩn: \(s = \sqrt {{s^2}} \).
a) Sai. Số lần chạy từ 12 giây trở lên là 0.
b) Sai. Thời gian chạy trung bình của vận động viên là:
\(\overline x = \frac{{3.10,2 + 8.10,6 + 6.11 + 2.11,4 + 1.11,8}}{{3 + 8 + 6 + 2 + 1}} = \frac{{54}}{5} = 10,8\) (giây).
c) Đúng. Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{3.{{\left( {10,2 - 10,8} \right)}^2} + 8.{{\left( {10,6 - 10,8} \right)}^2} + 6.{{\left( {11 - 10,8} \right)}^2} + 2.{{\left( {11,4 - 10,8} \right)}^2} + 1.{{\left( {11,8 - 10,8} \right)}^2}}}{{3 + 8 + 6 + 2 + 1}} = 0,168\).
d) Sai. Độ lệch chuẩn của mẫu số liệu trên là \(s = \sqrt {0,168} \approx 0,4\).
Một vât được phóng thẳng đứng lên trên từ mặt đất với tốc độ ban đầu là 32,5 m/s (bỏ qua sức cản của không khí), độ cao (tính bằng mét) của vật sau t giây được cho bởi công thức \(h(t) = 32,5t - 4,9{t^2}\). Vận tốc của vật sau 3 giây bằng bao nhiêu m/s?
Đáp án:
Đáp án:
Tính \(v(3) = h'(3)\).
Vận tốc của vật sau t giây là \(v(t) = h'(t) = 32,5 - 9,8t\) (m/s).
Vận tốc của vật sau 3 giây là \(v(3) = 32,5 - 9,8.3 = 3,1\) (m/s).
Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh x (cm), chiều cao là h (cm) và thể tích là 4000 \(c{m^3}\). Tìm độ dài cạnh hình vuông x sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.
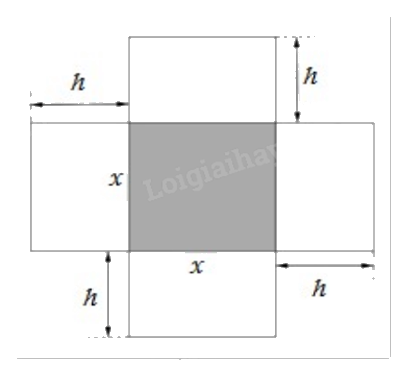
Đáp án:
Đáp án:
Lập hàm biểu diễn diện tích xung quanh và đáy của hộp rồi tìm giá trị nhỏ nhất của hàm đó.
Thể tích của hộp là \(V = {x^2}h = 4000\) (\(c{m^3}\)).
Suy ra chiều cao của hộp là \(h = \frac{{4000}}{{{x^2}}}\) (cm).
Diện tích xung quanh của hộp là \(S(x) = {x^2} + 4xh = {x^2} + 4x\frac{{4000}}{{{x^2}}} = {x^2} + \frac{{16000}}{x}\) (\(c{m^2}\)).
Chiếc hộp làm ra tốn ít bìa nhất khi diện tích xung quanh hình hộp nhỏ nhất.
Ta cần tìm giá trị nhỏ nhất của S(x).
Ta có \(S'(x) = 2x - \frac{{16000}}{{{x^2}}} = 0 \Leftrightarrow 2x = \frac{{16000}}{{{x^2}}} \Leftrightarrow 2{x^3} = 16000 \Leftrightarrow {x^3} = 8000 \Leftrightarrow x = 20\).
Ta có bảng biến thiên:
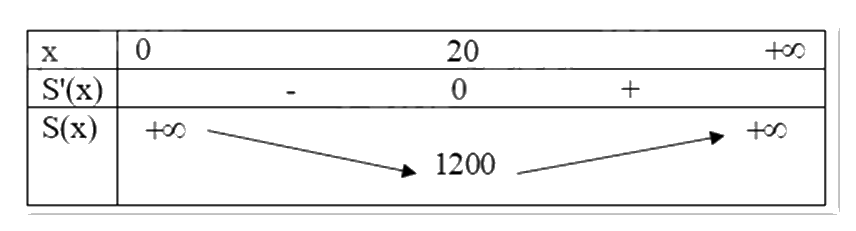
Vậy để tốn ít bìa nhất thì cạnh hình vuông có chiều dài x = 20 (cm).
Trong Vật lý, ta biết rằng khi mắc song song hai điện trở \({R_1}\) và \({R_2}\), thì điện trở tương đương R của mạch điện được tính theo công thức \(R = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) (theo Vật lý đại cương, NXB Giáo dục Việt Nam, 2016). Giả sử một điện trở \(10\Omega \) được mắc song song với một biến trở x thì điện trở tương đường R là hàm số \(\)\(y = \frac{{10x}}{{10 + x}}\) với x > 0. Điện trở tương đương của mạch không thể vượt quá bao nhiêu?
Đáp án:
Đáp án:
Tìm giới hạn của hàm số khi x tiến tới vô cực.
Ta có: Một điện trở \(10\Omega \) được mắc song song với một biến trở x nên điện trở tương đương là hàm số \(y = \frac{{10x}}{{10 + x}}\) với x > 0.
Vì \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{10x}}{{10 + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{10}}{{\frac{{10}}{x} + 1}} = \frac{{10}}{{0 + 1}} = 10\) nên điện trở tương đương của mạch không thể vượt quá \(10\Omega \).
Một chiếc cân đòn tay đang cân một vật có khối lượng m = 3 kg được thiết kế với đĩa cân được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có \(\widehat {ASC} = {90^o}\). Biết độ lớn của lực căng cho mỗi sợi xích có dạng \(\frac{{a\sqrt 2 }}{4}\). Lấy g = 10 \(m/{s^2}\), khi đó giá trị của a bằng bao nhiêu?
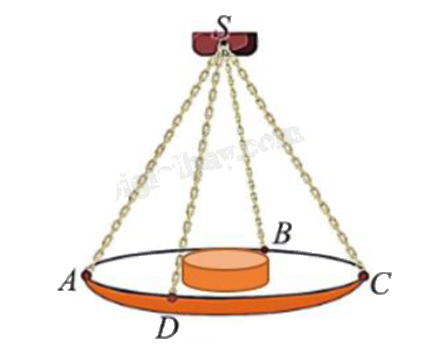
Đáp án:
Đáp án:
Sử dụng tính chất trung điểm, quy tắc nhân vecto với một số, cách xác định độ dài vecto, quy tắc tổng hợp lực.
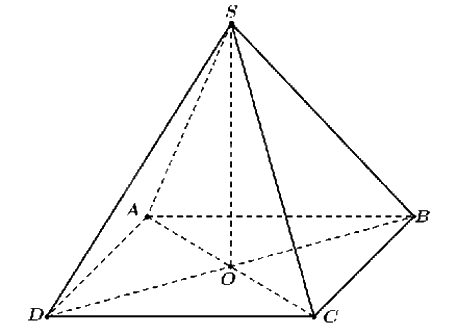
Gọi O là tâm hình vuông ABCD.
Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {OS} + \overrightarrow {SA} + \overrightarrow {OS} + \overrightarrow {SB} + \overrightarrow {OS} + \overrightarrow {SC} + \overrightarrow {OS} + \overrightarrow {SD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = - 4\overrightarrow {OS} = 4\overrightarrow {SO} \)
\( \Rightarrow \left| {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} } \right| = \left| {4\overrightarrow {SO} } \right| = 4SO\).
Trọng lượng của vật là \(P = mg = 3.10 = 30\)(N).
Suy ra \(4\left| {\overrightarrow {SO} } \right| = P = 30\)(N). Do đó \(SO = \frac{{30}}{4} = \frac{{15}}{2}\).
Vì tam giác ASC vuông cân tại S nên \(\widehat {SAC} = {45^o}\).
Xét tam giác SAO vuông tại O:
\(\sin \widehat {SAC} = \frac{{SO}}{{SA}} \Rightarrow SA = \frac{{SO}}{{\sin \widehat {SAC}}} = \frac{{\frac{{15}}{2}}}{{\sin {{45}^o}}} = \frac{{30\sqrt 2 }}{4}\).
Suy ra a = 30.
Hai chiếc khinh khí cầu bay lên từ cùng một địa điểm. Chiếc thứ nhất nằm cách điểm xuất phát 2,5 km về phía nam và 2 km về phía đông, đồng thời cách mặt đất 0,8 km. Chiếc thứ hai nằm cách điểm xuất phát 1,5 km về phía bắc và 3 km về phía tây, đồng thời cách mặt đất 0,6 km. Người ta cần tìm một vị trí trên mặt đất để tiếp nhiên liệu cho hai khinh khí cầu sao cho tổng khoảng cách từ vị trí đó tới hai khinh khí cầu nhỏ nhất. Giả sử vị trí cần tìm cách địa điểm hai khinh khí cầu bay lên là a km theo hướng nam và b km theo hướng tây. Tính tổng 2a + 3b.
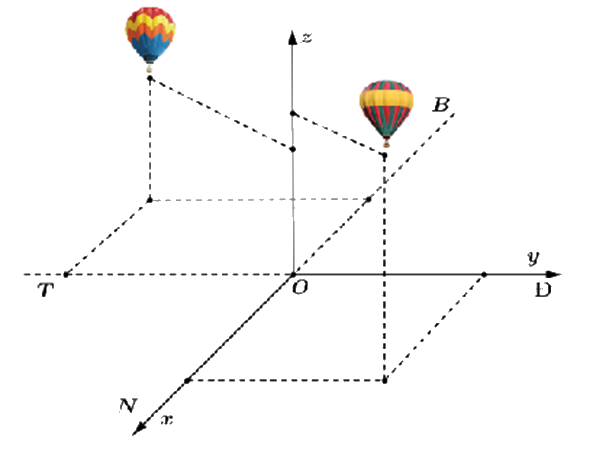
Đáp án:
Đáp án:
Sử dụng quy tắc tính tọa độ vecto, tính độ dài vecto.
Chọn hệ trục tọa độ Oxyz với gốc O đặt tại điểm xuất phát của hai khinh khí cầu, mặt phẳng (Oxy) trùng với mặt đất với trục Ox hướng về phía nam, trục Oy hướng về phía đông và trục Oz hướng thẳng đứng lên trời (tham khảo hình vẽ), đơn vị đo lấy theo kilômét.
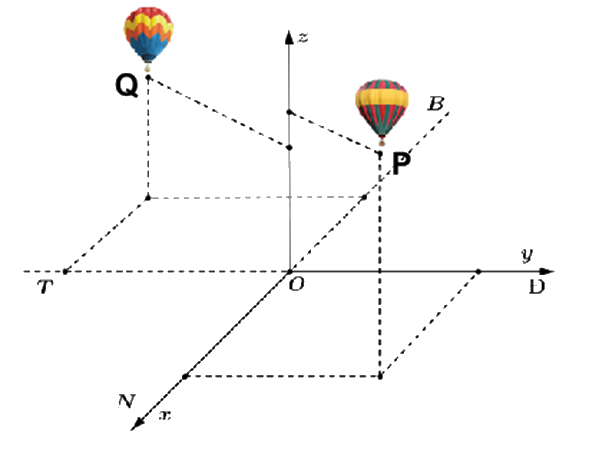
Gọi vị trí chiếc khinh khí cầu thứ nhất và thứ hai lần lượt là P, Q.
Khi đó: \(P\left( {\frac{5}{2};2;\frac{4}{5}} \right)\), \(Q\left( { - \frac{3}{2}; - 3;\frac{3}{5}} \right)\).
Gọi I là điểm tiếp nhiên liệu trên mặt đất (Oxy). Khi đó I\(({x_I};{y_I};0)\).
Khoảng cách từ vị trí tiếp nhiên liệu tới hai khinh khí cầu nhỏ nhất, tức là IP + IQ nhỏ nhất.
Gọi C là điểm đối xứng của P qua (Oxy). Khi đó \(C\left( {\frac{5}{2};2; - \frac{4}{5}} \right)\) và IP = IC.
Vậy để IP + IQ nhỏ nhất thì IC + IQ nhỏ nhất. Điều đó xảy ra khi Q, I, C thẳng hàng, hay \(\overrightarrow {QC} \), \(\overrightarrow {QI} \) cùng phương.
\(\overrightarrow {QC} = \left( {\frac{5}{2} + \frac{3}{2};2 + 3; - \frac{4}{5} - \frac{3}{5}} \right) = \left( {4;5; - \frac{7}{5}} \right)\); \(\overrightarrow {QI} = \left( {{x_I} + \frac{3}{2};{y_I} + 3; - \frac{3}{5}} \right)\).
Để \(\overrightarrow {QC} \), \(\overrightarrow {QI} \) cùng phương thì \(\frac{{{x_I} + \frac{3}{2}}}{4} = \frac{{{y_I} + 3}}{5} = \frac{3}{7}\). Từ đó tính được \({x_I} = \frac{3}{{14}}\); \({y_I} = - \frac{6}{7}\).
Vậy \(I\left( {\frac{3}{{14}};-\frac{6}{7};0} \right)\), suy ra \(a = \frac{3}{{14}}\); \(b = \frac{6}{7}\) (vì I cách điểm xuất phát b (km) theo hướng tây nên b > 0).
Ta được \(2a + 3b = 2.\frac{3}{{14}} + 3.\frac{6}{7} = 3\).
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Tính khoảng tứ phân vị của mẫu số liệu.
Đáp án:
Đáp án:
Tứ phân vị thứ i, kí hiệu là \({Q_i}\) với i = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_i} = {u_m} + \frac{{\frac{{in}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\).
Trong đó:
\(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu.
\([{u_m};{u_{m + 1}})\) là nhóm chứa tứ phân vị thứ i.
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ i.
\(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1}\).
Cỡ mẫu: n = 4 + 8 + 12 + 10 + 6 = 40.
Giả sử mẫu số liệu gốc là \({x_1},{x_2},...,{x_{40}}\) được sắp xếp theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{{{x_{10}} + {x_{11}}}}{2} \in [20;40)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là \({Q_1} = 20 + \frac{{\frac{{40}}{4} - 4}}{8}(40 - 20) = 35\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{{{x_{30}} + {x_{31}}}}{2} \in [60;80)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là \({Q_3} = 60 + \frac{{\frac{{3.40}}{4} - (4 + 8 + 12)}}{{10}}(80 - 60) = 72\).
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 72 - 35 = 37\).
Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5: Tổng quan và Hướng dẫn Ôn tập
Chào mừng các em học sinh lớp 12 đến với bài viết tổng quan về Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5 do tusach.vn cung cấp. Bài viết này sẽ cung cấp thông tin chi tiết về cấu trúc đề thi, các chủ đề trọng tâm, và hướng dẫn ôn tập hiệu quả để các em đạt kết quả tốt nhất trong kỳ thi sắp tới.
Cấu trúc Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5
Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5 thường bao gồm các phần sau:
- Phần trắc nghiệm: Khoảng 20-30% tổng số điểm, tập trung vào các kiến thức cơ bản và khả năng vận dụng nhanh.
- Phần tự luận: Khoảng 70-80% tổng số điểm, bao gồm các câu hỏi về đại số, hình học, và giải tích.
Các Chủ đề Trọng tâm
Để chuẩn bị tốt nhất cho kỳ thi, các em cần tập trung ôn tập các chủ đề sau:
- Đại số:
- Hàm số bậc nhất, bậc hai
- Phương trình, bất phương trình
- Dãy số, cấp số cộng, cấp số nhân
- Hình học:
- Vecto trong mặt phẳng
- Phương trình đường thẳng, đường tròn
- Hình học không gian (khối đa diện)
- Giải tích:
- Giới hạn
- Đạo hàm
- Tích phân
Hướng dẫn Ôn tập Hiệu quả
Dưới đây là một số lời khuyên giúp các em ôn tập hiệu quả:
- Nắm vững kiến thức cơ bản: Đây là nền tảng quan trọng để giải quyết các bài toán phức tạp.
- Luyện tập thường xuyên: Giải nhiều đề thi và bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải đề.
- Sử dụng tài liệu ôn tập chất lượng: Chọn các tài liệu ôn tập uy tín và được cập nhật thường xuyên.
- Tìm kiếm sự giúp đỡ khi cần thiết: Đừng ngần ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn trong quá trình học tập.
Tại sao nên chọn Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5 của tusach.vn?
Tusach.vn cam kết cung cấp:
- Đề thi được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
- Đáp án chi tiết, dễ hiểu, giúp học sinh tự đánh giá năng lực.
- Cập nhật liên tục các đề thi mới nhất.
- Giao diện thân thiện, dễ sử dụng.
Tải ngay Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5
Hãy truy cập tusach.vn để tải ngay Đề thi học kì 1 Toán 12 Chân trời sáng tạo - Đề số 5 và bắt đầu luyện thi ngay hôm nay! Chúc các em đạt kết quả cao nhất trong kỳ thi sắp tới.
| Chủ đề | Mức độ quan trọng |
|---|---|
| Hàm số | Cao |
| Đạo hàm | Cao |
| Vecto | Trung bình |
| Nguồn: tusach.vn | |