Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 6
Tổng quan nội dung
Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 6
Tusach.vn xin giới thiệu Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 6, được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các câu hỏi trắc nghiệm và tự luận, tập trung vào các chủ đề quan trọng trong chương trình học kì 1. Kèm theo đề thi là đáp án chi tiết, giúp học sinh tự đánh giá kết quả và rút kinh nghiệm.
Đề bài
Hàm số nào sau đây có tập xác định \(\mathbb{R}\)?
- A.
\(y = \tan x\)
- B.
\(y = \cot x\)
- C.
\(y = \frac{1}{{{{\sin }^2}x + 1}}\)
- D.
\(y = \frac{1}{{\cot x}}\)
Tổng các nghiệm của phương trình \(\tan (2x - {15^o}) = 1\) trên khoảng \(( - {90^o};{90^o})\) bằng
- A.
\({30^o}\)
- B.
\( - {60^o}\)
- C.
\({0^o}\)
- D.
\( - {30^o}\)
Cho dãy số \(\left( {{u_n}} \right) = {2024^n}\). Tính \({u_{n + 1}}\)?
- A.
\({u_{n + 1}} = {2024^n} + 2024\)
- B.
\({u_{n + 1}} = {2024^n} + 1\)
- C.
\({u_{n + 1}} = {2024^{n + 1}}\)
- D.
\({u_{n + 1}} = 2024(n + 1)\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và công sai d = -5. Khi đó –32 là số hạng thứ mấy của cấp số cộng đã cho?
- A.
7
- B.
10
- C.
9
- D.
8
Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu \({u_1} = 1\), công bội q = 2. Tổng ba số hạng đầu của cấp số nhân là
- A.
3
- B.
7
- C.
9
- D.
5
Phát biểu nào sau đây là sai?
- A.
\(\lim {u_n} = c\) (\({u_n} = c\) là hằng số)
- B.
\(\lim {q^n} = 0\) \(\left( {\left| q \right| > 1} \right)\)
- C.
\(\lim \frac{1}{n} = 0\)
- D.
\(\lim \frac{1}{{{n^k}}} = 0\) \((k > 1)\)
Hàm số \(y = \frac{1}{{2x - 4}}\) gián đoạn tại điểm nào dưới đây?
- A.
x = 1
- B.
x = 0
- C.
x = 2
- D.
x = -1
Trong các mệnh đề sau đây, mệnh đề nào sai?
- A.
Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa
- B.
Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất
- C.
Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất
- D.
Hai mặt phẳng cùng đi qua 3 điểm A, B, C không thẳng hàng thì hai mặt phẳng đó trùng nhau
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Gọi M, N lần lượt là trung điểm của SA và SC. Khẳng định nào sau đây đúng?
- A.
MN//(ABCD)
- B.
AB//(SCD)
- C.
BC//(SAD)
- D.
MN//(SBD)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi E là trung điểm của SA. Mặt phẳng nào dưới đây chứa đường thẳng OE?
- A.
(SBC)
- B.
(ABCD)
- C.
(SAC)
- D.
(CDE)
Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau:
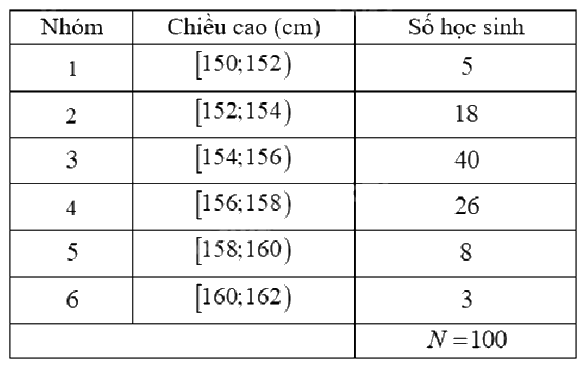
Giá trị đại diện của nhóm thứ tư là
- A.
156,5
- B.
157
- C.
157,5
- D.
158
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Nhóm chứa trung vị của mẫu số liệu trên là
- A.
[40;60)
- B.
[20;40)
- C.
[60;80)
- D.
[80;100)
Cho phương trình \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\).
a) Phương trình đã cho được viết lại như sau: \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
b) Ta có \(\cos (2x + \pi ) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\) \((k \in \mathbb{Z})\).
Biết \(\lim \frac{{2{n^2} - n + 4}}{{a{n^2} + n + 3}} = 2\) và \(\lim \frac{{{3^n} + {4^{n + 1}}}}{{{4^n} + 3}} = b\).
a) Giá trị của a = 2.
b) Giá trị của b = 4.
c) a; 2; b lập thành một cấp số cộng.
d) a; b; 16 lập thành một cấp số nhân.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy P sao cho BP = 2PD.
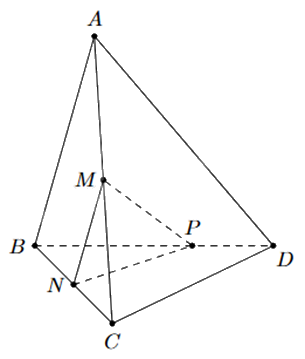
a) Gọi \(I = CD \cap (MNP)\). Ba điểm I, N, P thẳng hàng.
b) MN//(ABD).
c) Giao tuyến của hai mặt phẳng (MNP) và (ABD) là đường thẳng PQ song song với AB, với Q thuộc AD.
d) Tứ giác MNPQ là hình bình hành.
Trong một đề tài nghiên cứu về bệnh A, người ta ghi lại tuổi của bệnh nhân mắc bệnh này, số liệu thống kê được trình bày trong bảng sau:

a) Cỡ mẫu là n = 50.
b) Nhóm chứa mốt của mẫu số liệu là [55;65).
c) Trung vị của mẫu số liệu thuộc nhóm [25;35).
d) Trung vị của mẫu số liệu gần bằng 37,14.
Hằng ngày mức nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mức nước trong kênh được tính tại thời điểm t (giờ) trong một ngày (t > 0) bởi công thức \(h = 4\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) + 16\). Mực nước của kênh cao nhất khi t bằng bao nhiêu?
Đáp án:
Một rạp hát có 18 hàng ghế xếp theo hình quạt. Hàng thứ nhất có 16 ghế, hàng thứ hai có 20 ghế, hàng thứ ba có 24 ghế,... cứ thế cho đến hàng cuối cùng. Hỏi tổng số ghế có trong rạp là bao nhiêu?
Đáp án:
Tính giới hạn \(\lim \left[ {\frac{1}{{1.3}} + \frac{1}{{3.5}} + \frac{1}{{5.7}} + ... + \frac{1}{{(2n - 1)(2n + 1)}}} \right]\). Viết kết quả dưới dạng số thập phân.
Đáp án:
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{\sqrt[3]{{x + 7}} - \sqrt {3x + 1} }}{{x - 1}}\\ax\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ne 1\\x = 1\end{array}\). Tìm giá trị của a để hàm số liên tục tại \({x_0} = 1\) (làm tròn kết quả đến hàng phần mười).
Đáp án:
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC và BD, AC = 6, BD = 8; tam giác SBD là tam giác đều. Gọi I là điểm nằm trên đoạn thẳng AC sao cho AI = x (0 < x < 3), (P) là mặt phẳng đi qua điểm I và song song với mặt phẳng (SBD). Diện tích của hình tạo bởi các đoạn giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD bằng \(\frac{{a{x^2}\sqrt 3 }}{b}\). Tính giá trị của biểu thức P = a + b.
Đáp án:
Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu sau:

Hãy cho biết 75% học sinh khối 11 ngủ nhiều nhất bao nhiêu giờ?
Đáp án:
Lời giải và đáp án
Hàm số nào sau đây có tập xác định \(\mathbb{R}\)?
- A.
\(y = \tan x\)
- B.
\(y = \cot x\)
- C.
\(y = \frac{1}{{{{\sin }^2}x + 1}}\)
- D.
\(y = \frac{1}{{\cot x}}\)
Đáp án : C
Tìm tập xác định của từng hàm số.
Hàm số \(y = \tan x\) xác định \(\forall x \ne \frac{\pi }{2} + k\pi \) \(\left( {k \in \mathbb{Z}} \right)\).
Hàm số \(y = \cot x\) xác định \(\forall x \ne k\pi \) \(\left( {k \in \mathbb{Z}} \right)\).
Hàm số \(y = \frac{1}{{\cot x}}\) xác định \(\forall x \ne \frac{{k\pi }}{2}\) \(\left( {k \in \mathbb{Z}} \right)\).
Hàm số \(y = \frac{1}{{{{\sin }^2}x + 1}}\) xác định với mọi giá trị của x.
Tổng các nghiệm của phương trình \(\tan (2x - {15^o}) = 1\) trên khoảng \(( - {90^o};{90^o})\) bằng
- A.
\({30^o}\)
- B.
\( - {60^o}\)
- C.
\({0^o}\)
- D.
\( - {30^o}\)
Đáp án : D
\(\tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \) \((k \in \mathbb{Z})\).
\(\tan (2x - {15^o}) = 1 \Leftrightarrow 2x - {15^o} = {45^o} + k{180^o} \Leftrightarrow x = {30^o} + k{90^o}\) \((k \in \mathbb{Z})\).
Xét \( - {90^o} < x < {90^o} \Leftrightarrow - {90^o} < {30^o} + k{90^o} < {90^o} \Leftrightarrow - \frac{4}{3} < k < \frac{2}{3}\).
Suy ra k = -1 hoặc k = 0.
Với k = -1, ta được \(x = - {60^o}\).
Với k = 0, ta được \(x = {30^o}\).
Vậy tổng các nghiệm là \( - {60^o} + {30^o} = - {30^o}\).
Cho dãy số \(\left( {{u_n}} \right) = {2024^n}\). Tính \({u_{n + 1}}\)?
- A.
\({u_{n + 1}} = {2024^n} + 2024\)
- B.
\({u_{n + 1}} = {2024^n} + 1\)
- C.
\({u_{n + 1}} = {2024^{n + 1}}\)
- D.
\({u_{n + 1}} = 2024(n + 1)\)
Đáp án : C
Thay n + 1 vào n.
Ta có \({u_{n + 1}} = {2024^{n + 1}}\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và công sai d = -5. Khi đó –32 là số hạng thứ mấy của cấp số cộng đã cho?
- A.
7
- B.
10
- C.
9
- D.
8
Đáp án : D
Công thức số hạng tổng quát: \({u_n} = {u_1} + (n - 1)d\).
-32 là số hạng thứ n của cấp số cộng. Ta có \(32 = 3 + (n - 1)( - 5) \Leftrightarrow n = 8\).
Cho dãy số \(\left( {{u_n}} \right)\) là cấp số nhân có số hạng đầu \({u_1} = 1\), công bội q = 2. Tổng ba số hạng đầu của cấp số nhân là
- A.
3
- B.
7
- C.
9
- D.
5
Đáp án : B
Công thức tổng n số hạng đầu của cấp số nhân: \({S_n} = {u_1}\frac{{1 - {q^n}}}{{1 - q}}\).
Áp dụng công thức tổng số hạng của cấp số nhân ta có: \({S_3} = 1.\frac{{1 - {2^3}}}{{1 - 2}} = 7\).
Phát biểu nào sau đây là sai?
- A.
\(\lim {u_n} = c\) (\({u_n} = c\) là hằng số)
- B.
\(\lim {q^n} = 0\) \(\left( {\left| q \right| > 1} \right)\)
- C.
\(\lim \frac{1}{n} = 0\)
- D.
\(\lim \frac{1}{{{n^k}}} = 0\) \((k > 1)\)
Đáp án : B
Theo định nghĩa giới hạn hữu hạn của dãy số.
Ta có \(\lim {q^n} = 0\) \(\left( {\left| q \right| < 1} \right)\) nên B sai.
Hàm số \(y = \frac{1}{{2x - 4}}\) gián đoạn tại điểm nào dưới đây?
- A.
x = 1
- B.
x = 0
- C.
x = 2
- D.
x = -1
Đáp án : C
Tìm điểm mà tại đó hàm số không xác định
Hàm số có tập xác định là \(D = \mathbb{R}\backslash \{ 2\} \), suy ra hàm số gián đoạn tại x = 2.
Trong các mệnh đề sau đây, mệnh đề nào sai?
- A.
Hai mặt phẳng có một điểm chung thì chúng có vô số điểm chung khác nữa
- B.
Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất
- C.
Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất
- D.
Hai mặt phẳng cùng đi qua 3 điểm A, B, C không thẳng hàng thì hai mặt phẳng đó trùng nhau
Đáp án : B
Sử dụng kiến thức về vị trí tương đối giữa hai mặt phẳng.
B sai vì hai mặt phẳng có một điểm chung thì chúng có thể trùng nhau. Khi đó chúng có vô số điểm chung và chung nhau vô số đường thẳng.
Cho hình chóp S.ABCD có đáy ABCD là tứ giác lồi. Gọi M, N lần lượt là trung điểm của SA và SC. Khẳng định nào sau đây đúng?
- A.
MN//(ABCD)
- B.
AB//(SCD)
- C.
BC//(SAD)
- D.
MN//(SBD)
Đáp án : A
Đường thẳng song song với mặt phẳng nếu nó song song với một đường thuộc mặt phẳng đó.
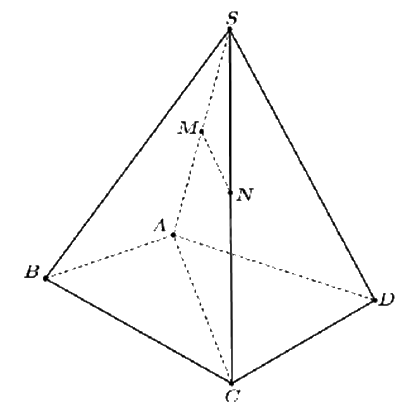
Vì MN là đường trung bình của tam giác SAC nên MN//AC.
Mà AC thuộc mặt phẳng (ABCD) suy ra MN//(ABCD).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi E là trung điểm của SA. Mặt phẳng nào dưới đây chứa đường thẳng OE?
- A.
(SBC)
- B.
(ABCD)
- C.
(SAC)
- D.
(CDE)
Đáp án : C
Mặt phẳng cần tìm chứa cả hai điểm O và E.
Ta có \(\left\{ \begin{array}{l}O \in AC\\E \in SA\end{array} \right.\) nên \(OE \subset (SAC)\).
Điều tra về chiều cao của học sinh khối lớp 11, ta có kết quả sau:
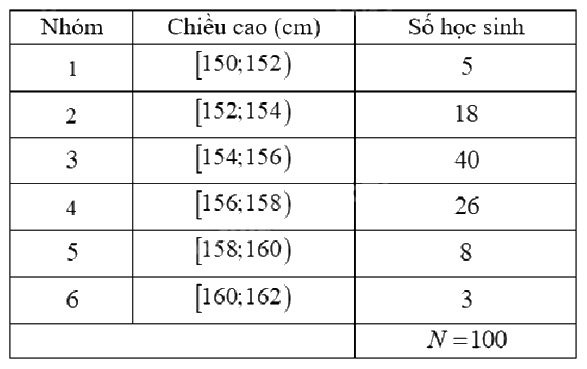
Giá trị đại diện của nhóm thứ tư là
- A.
156,5
- B.
157
- C.
157,5
- D.
158
Đáp án : B
Giá trị đại diện của nhóm là trung bình cộng của đầu mút trái và đầu mút phải nhóm đó.
Giá trị đại diện của nhóm thứ tư là \(\frac{{156 + 158}}{2} = 157\).
Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Nhóm chứa trung vị của mẫu số liệu trên là
- A.
[40;60)
- B.
[20;40)
- C.
[60;80)
- D.
[80;100)
Đáp án : A
Nhóm chứa trung vị là nhóm chứa giá trị chính giữa của mẫu số liệu.
Cỡ mẫu: n = 5 + 9 + 12 + 10 + 6 = 42.
Trung vị của mẫu số liệu trên là \({Q_2} = \frac{{{x_{21}} + {x_{22}}}}{2}\).
Mà \({x_{21}}\), \({x_{22}}\) \( \in [40;60)\).
Vậy nhóm chứa trung vị của mẫu số liệu trên là [40;60).
Cho phương trình \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\).
a) Phương trình đã cho được viết lại như sau: \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
b) Ta có \(\cos (2x + \pi ) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\) \((k \in \mathbb{Z})\).
a) Phương trình đã cho được viết lại như sau: \({\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)\).
b) Ta có \(\cos (2x + \pi ) = - \cos 2x\).
c) Phương trình đã cho đưa về dạng \(\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x\).
d) Nghiệm của phương trình đã cho là \(x = - \frac{\pi }{4} + k\pi \) và \(x = \frac{\pi }{{12}} + k\frac{\pi }{3}\) \((k \in \mathbb{Z})\).
a) Sử dụng công thức \({\sin ^2}x + {\cos ^2}x = 1\).
b) Sử dụng công thức \(\cos (x + \pi ) = - \cos x\).
c) Sử dụng công thức hạ bậc \({\sin ^2}x = \frac{{1 - \cos 2x}}{2}\), \({\cos ^2}x = \frac{{\cos 2x + 1}}{2}\).
d) Sử dụng công thức nghiệm của phương trình lượng giác cơ bản:
\(\cos x = \cos \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
a) Đúng. Ta có: \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\)
\( \Leftrightarrow {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1 - {\cos ^2}\left( {2x + \frac{\pi }{4}} \right)\)
\( \Leftrightarrow {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = {\sin ^2}\left( {2x + \frac{\pi }{4}} \right)\).
b) Đúng. \(\cos (2x + \pi ) = - \cos 2x\).
c) Đúng. Ta có: \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1\)
\( \Leftrightarrow {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = {\sin ^2}\left( {2x + \frac{\pi }{4}} \right)\)
\( \Leftrightarrow \frac{{\cos \left( {2x + \pi } \right) + 1}}{2} = \frac{{1 - \cos \left( {4x + \frac{\pi }{2}} \right)}}{2}\)
\( \Leftrightarrow \cos \left( {2x + \pi } \right) = - \cos \left( {4x + \frac{\pi }{2}} \right)\)
\( \Leftrightarrow - \cos 2x = - \cos \left( {4x + \frac{\pi }{2}} \right)\)
\( \Leftrightarrow \cos 2x = \cos \left( {4x + \frac{\pi }{2}} \right)\).
d) Sai. Ta có: \({\cos ^2}\left( {2x + \frac{\pi }{4}} \right) + {\cos ^2}\left( {x + \frac{\pi }{2}} \right) = 1 \Leftrightarrow \cos 2x = \cos \left( {4x + \frac{\pi }{2}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}2x = 4x + \frac{\pi }{2} + k2\pi \\2x = - 4x - \frac{\pi }{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 4x + \frac{\pi }{2} + k2\pi \\2x = - 4x - \frac{\pi }{2} + k2\pi \end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l} - 2x = \frac{\pi }{2} + k2\pi \\6x = - \frac{\pi }{2} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - \frac{\pi }{4} + k\pi \\x = - \frac{\pi }{{12}} + k\frac{\pi }{3}\end{array} \right.\) \((k \in \mathbb{Z})\).
Biết \(\lim \frac{{2{n^2} - n + 4}}{{a{n^2} + n + 3}} = 2\) và \(\lim \frac{{{3^n} + {4^{n + 1}}}}{{{4^n} + 3}} = b\).
a) Giá trị của a = 2.
b) Giá trị của b = 4.
c) a; 2; b lập thành một cấp số cộng.
d) a; b; 16 lập thành một cấp số nhân.
a) Giá trị của a = 2.
b) Giá trị của b = 4.
c) a; 2; b lập thành một cấp số cộng.
d) a; b; 16 lập thành một cấp số nhân.
Sử dụng các quy tắc tìm giới hạn của dãy số.
a) Sai. Ta có: \(\lim \frac{{2{n^2} - n + 4}}{{a{n^2} + n + 3}} = \lim \frac{{{n^2}\left( {2 - \frac{1}{n} + \frac{4}{{{n^2}}}} \right)}}{{{n^2}\left( {a + \frac{1}{n} + \frac{3}{{{n^2}}}} \right)}} = \lim \frac{{2 - \frac{1}{n} + \frac{4}{{{n^2}}}}}{{a + \frac{1}{n} + \frac{3}{{{n^2}}}}} = \frac{2}{a} = 2\).
Suy ra a = 1.
b) Đúng. Ta có: \(\lim \frac{{{3^n} + {4^{n + 1}}}}{{{4^n} + 3}} = \lim \frac{{{3^n} + {4^n}.4}}{{{4^n} + 3}} = \lim \frac{{{{\left( {\frac{3}{4}} \right)}^n} + 4}}{{1 + 3.{{\left( {\frac{1}{4}} \right)}^n}}} = \frac{{0 + 4}}{{1 + 0}} = 4 = b\).
c) Sai. 1; 2; 4 không lập thành một cấp số cộng.
d) Đúng. 1; 4; 16 lập thành một cấp số nhân với số hạng đầu là 1, công bội bằng 4.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC. Trên đoạn BD lấy P sao cho BP = 2PD.
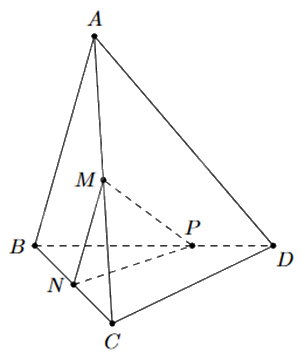
a) Gọi \(I = CD \cap (MNP)\). Ba điểm I, N, P thẳng hàng.
b) MN//(ABD).
c) Giao tuyến của hai mặt phẳng (MNP) và (ABD) là đường thẳng PQ song song với AB, với Q thuộc AD.
d) Tứ giác MNPQ là hình bình hành.
a) Gọi \(I = CD \cap (MNP)\). Ba điểm I, N, P thẳng hàng.
b) MN//(ABD).
c) Giao tuyến của hai mặt phẳng (MNP) và (ABD) là đường thẳng PQ song song với AB, với Q thuộc AD.
d) Tứ giác MNPQ là hình bình hành.
Sử dụng các điều kiện, tính chất của đường thẳng và mặt phẳng song song.
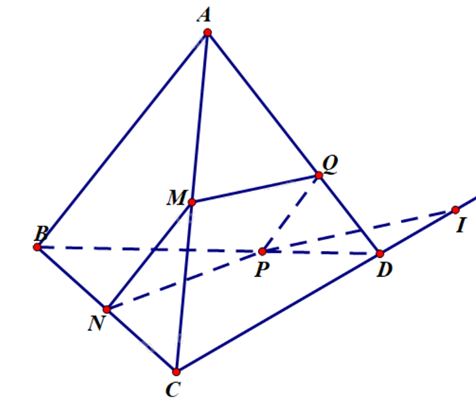
a) Sai. Xét trong mặt phẳng (BCD):
Vì NP không song song với CD nên giả sử NP giao CD tại O.
Khi đó \(\left\{ \begin{array}{l}O \in CD\\O \in NP \subset (MNP)\end{array} \right.\) nên \(O = CD \cap (MNP)\).
Vậy \(O \equiv I\). Vì \(O \in NP\) suy ra I, N, P thẳng hàng.
b) Đúng. Vì MN là đường trung bình của tam giác ABC nên MN//AB.
c) Đúng. Ta có \(\left\{ \begin{array}{l}MN//AB\\MN \subset (MNP)\\AB \subset (ABD)\\(MNP) \cap (ABD) = \{ P\} \end{array} \right.\) suy ra giao tuyến của (MNP) và (ABD) là đường thẳng qua P và song song với AB, MN.
Theo giả thiết, PQ//AB nên PQ chính là giao tuyến cần tìm.
d) Sai. Vì MN là đường trung bình của tam giác ABC nên \(MN = \frac{1}{2}AB\) (1).
Theo giả thiết, BP = 2PD nên suy ra \(\frac{{DP}}{{DB}} = \frac{1}{3}\).
Xét tam giác ABD có PQ//AB:
\(\frac{{DQ}}{{DA}} = \frac{{DP}}{{DB}} = \frac{{PQ}}{{AB}} = \frac{1}{3}\) (hệ quả định lý Thales).
Suy ra \(PQ = \frac{1}{3}AB\) (2).
Từ (1) và (2) suy ra \(MN \ne PQ\).
Vậy MNPQ không phải hình bình hành.
Trong một đề tài nghiên cứu về bệnh A, người ta ghi lại tuổi của bệnh nhân mắc bệnh này, số liệu thống kê được trình bày trong bảng sau:

a) Cỡ mẫu là n = 50.
b) Nhóm chứa mốt của mẫu số liệu là [55;65).
c) Trung vị của mẫu số liệu thuộc nhóm [25;35).
d) Trung vị của mẫu số liệu gần bằng 37,14.
a) Cỡ mẫu là n = 50.
b) Nhóm chứa mốt của mẫu số liệu là [55;65).
c) Trung vị của mẫu số liệu thuộc nhóm [25;35).
d) Trung vị của mẫu số liệu gần bằng 37,14.
a) Cỡ mẫu bằng tổng tần số trong bảng số liệu.
b) Nhóm chứa mốt có tần số lớn nhất trong bảng số liệu.
c) Trung vị là giá trị chính giữa trong các giá trị sắp xếp theo thứ tự không giảm.
d) Công thức tính trung vị: \({M_e} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.({u_{m + 1}} - {u_m})\).
a) Đúng. n = 10 + 12 + 14 + 9 + 5 = 50.
b) Sai. Nhóm chứa mốt là [35;45).
c) Sai. Ta có \(\frac{n}{2} = 25\) nên trung vị là \({M_e} = \frac{{{x_{25}} + {x_{26}}}}{2} \in [35;45)\).
d) Đúng. \({M_e} = 35 + \frac{{\frac{{50}}{2} - (10 + 12)}}{{14}}.(45 - 35) = \frac{{260}}{7} \approx 37,14\).
Hằng ngày mức nước của con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mức nước trong kênh được tính tại thời điểm t (giờ) trong một ngày (t > 0) bởi công thức \(h = 4\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) + 16\). Mực nước của kênh cao nhất khi t bằng bao nhiêu?
Đáp án:
Đáp án:
\(h = 4\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) + 16\) lớn nhất khi \(\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) = 1\).
Sử dụng công thức nghiệm của phương trình lượng giác cơ bản:
\(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\) \((k \in \mathbb{Z})\).
\(\sin \left( {\frac{{\pi t}}{8} + \frac{{5\pi }}{8}} \right) = 1 \Leftrightarrow \frac{{\pi t}}{8} + \frac{{5\pi }}{8} = \frac{\pi }{2} + k2\pi \Leftrightarrow \frac{{\pi t}}{8} = - \frac{\pi }{8} + k2\pi \)
\( \Leftrightarrow \frac{t}{8} = - \frac{1}{8} + 2k \Leftrightarrow t = - 1 + 16k\) \((k \in \mathbb{Z})\).
Ta có \(0 < t \le 24 \Leftrightarrow 0 < - 1 + 16k \le 24 \Leftrightarrow 1 < 16k \le 24 \Leftrightarrow \frac{1}{{16}} < k \le \frac{3}{2}\).
Vậy k = 1. Khi đó t = -1 + 16.1 = 15.
Vậy mực nước của kênh cao nhất khi t = 15 (giờ).
Một rạp hát có 18 hàng ghế xếp theo hình quạt. Hàng thứ nhất có 16 ghế, hàng thứ hai có 20 ghế, hàng thứ ba có 24 ghế,... cứ thế cho đến hàng cuối cùng. Hỏi tổng số ghế có trong rạp là bao nhiêu?
Đáp án:
Đáp án:
Sử dụng công thức tổng n số hạng đầu của cấp số cộng: \({S_n} = \frac{{n\left[ {2{u_1} + (n - 1)d} \right]}}{2}\).
Số ghế mỗi hàng lập thành một cấp số cộng với \({u_1} = 16\) và d = 4.
Tổng số ghế trong rạp là \({S_{18}} = \frac{{18\left[ {2.16 + (18 - 1).4} \right]}}{2} = 900\).
Tính giới hạn \(\lim \left[ {\frac{1}{{1.3}} + \frac{1}{{3.5}} + \frac{1}{{5.7}} + ... + \frac{1}{{(2n - 1)(2n + 1)}}} \right]\). Viết kết quả dưới dạng số thập phân.
Đáp án:
Đáp án:
Sử dụng quy tắc tính giới hạn tại vô cực.
\(\lim \left[ {\frac{1}{{1.3}} + \frac{1}{{3.5}} + \frac{1}{{5.7}} + ... + \frac{1}{{(2n - 1)(2n + 1)}}} \right]\)
\( = \lim \frac{1}{2}\left( {1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + ... + \frac{1}{{2n - 1}} + \frac{1}{{2n + 1}}} \right)\)
\( = \lim \frac{1}{2}\left( {1 - \frac{1}{{2n + 1}}} \right) = \frac{1}{2}\left( {1 - 0} \right) = \frac{1}{2} = 0,5\).
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{{\sqrt[3]{{x + 7}} - \sqrt {3x + 1} }}{{x - 1}}\\ax\end{array} \right.\) \(\begin{array}{l}khi\\khi\end{array}\) \(\begin{array}{l}x \ne 1\\x = 1\end{array}\). Tìm giá trị của a để hàm số liên tục tại \({x_0} = 1\) (làm tròn kết quả đến hàng phần mười).
Đáp án:
Đáp án:
Hàm số liên tục tại \({x_0}\) khi \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\).
Ta có: \(\frac{{\sqrt[3]{{x + 7}} - \sqrt {3x + 1} }}{{x - 1}} = \frac{{\sqrt[3]{{x + 7}} - 2 + 2 - \sqrt {3x + 1} }}{{x - 1}} = \frac{{\sqrt[3]{{x + 7}} - 2}}{{x - 1}} + \frac{{2 - \sqrt {3x + 1} }}{{x - 1}}\)
\( = \frac{{x + 7 - 8}}{{\left( {x - 1} \right)\left( {\sqrt {x + 7} + \sqrt[2]{{x + 7}}.2 + 4} \right)}} + \frac{{4 - \left( {3x + 1} \right)}}{{\left( {x - 1} \right)\left( {2 + \sqrt {3x + 1} } \right)}}\)
\( = \frac{1}{{\sqrt {x + 7} + \sqrt[2]{{x + 7}}.2 + 4}} + \frac{{3 - 3x}}{{\left( {x - 1} \right)\left( {2 + \sqrt {3x + 1} } \right)}}\)
\( = \frac{1}{{\sqrt {x + 7} + \sqrt[2]{{x + 7}}.2 + 4}} - \frac{3}{{2 + \sqrt {3x + 1} }}\).
Ta có: \(\mathop {\lim }\limits_{x \to 1} f(x) = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[3]{{x + 7}} - \sqrt {3x + 1} }}{{x - 1}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt {x + 7} + \sqrt[2]{{x + 7}}.2 + 4}} - \frac{3}{{2 + \sqrt {3x + 1} }}\)
\( = \frac{1}{{\sqrt {1 + 7} + \sqrt[2]{{1 + 7}}.2 + 4}} - \frac{3}{{2 + \sqrt {3.1 + 1} }} \approx - 0,7\).
Mà \(f(1) = a.1 = a\).
Để hàm số liên tục tại \({x_0} = 1\) thì \(\mathop {\lim }\limits_{x \to 1} f(x) = f(1)\), suy ra \(a \approx - 0,7\).
Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của AC và BD, AC = 6, BD = 8; tam giác SBD là tam giác đều. Gọi I là điểm nằm trên đoạn thẳng AC sao cho AI = x (0 < x < 3), (P) là mặt phẳng đi qua điểm I và song song với mặt phẳng (SBD). Diện tích của hình tạo bởi các đoạn giao tuyến của mặt phẳng (P) với các mặt của hình chóp S.ABCD bằng \(\frac{{a{x^2}\sqrt 3 }}{b}\). Tính giá trị của biểu thức P = a + b.
Đáp án:
Đáp án:
Sử dụng tính chất giao tuyến, hệ quả định lí Thales, công thức tính diện tích tam giác đều khi biết độ dài cạnh.
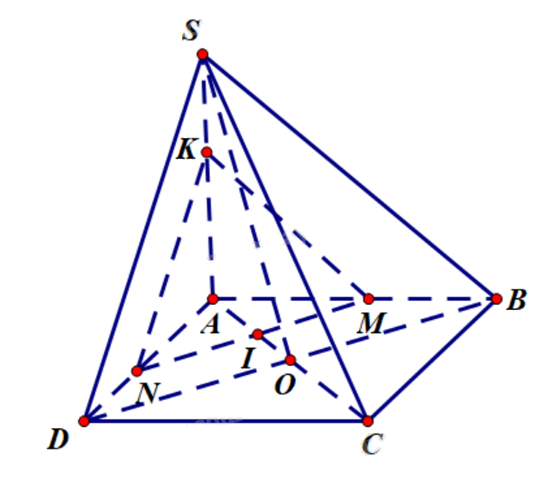
Vì (P)//(SBD) suy ra BD//(P) và SB//(P).
Ta có \(\left\{ \begin{array}{l}I \in (P) \cap (ABCD)\\BD \subset (ABCD)\\BD//(P)\end{array} \right.\) suy ra giao tuyến của (P) và (ABCD) là đường thẳng qua I song song với BD. Giao tuyến này cắt AB tại M, cắt AD tại N.
Tương tự \(\left\{ \begin{array}{l}M \in (P) \cap (SAB)\\SB \subset (SAB)\\SB//(P)\end{array} \right.\) suy ra giao tuyến của (P) và (SAB) là đường thẳng qua M song song với SB.
Giao tuyến này cắt SA tại K.
Thiết diện cần tìm là tam giác MNK.
Hai tam giác KMN và SBD có các cặp cạnh tương ứng song song nên chúng đồng dạng. Mà tam giác SBD đều nên tam giác KMN đều.
Xét tam giác AOD có IN//DO: \(\frac{{AI}}{{AO}} = \frac{{IN}}{{DO}}\) (hệ quả định lí Thales).
Xét tam giác AOB có IM//BO: \(\frac{{AI}}{{AO}} = \frac{{IM}}{{BO}}\) (hệ quả định lí Thales).
Suy ra \(\frac{{IN}}{{DO}} = \frac{{IM}}{{BO}}\). Do đó \(\frac{{AI}}{{AO}} = \frac{{IN + IM}}{{DO + BO}}\) hay \(\frac{{AI}}{{AO}} = \frac{{MN}}{{BD}} \Leftrightarrow \frac{x}{{\frac{{AC}}{2}}} = \frac{{MN}}{{BD}}\)
\( \Leftrightarrow \frac{x}{3} = \frac{{MN}}{8} \Leftrightarrow MN = \frac{{8x}}{3}\).
Diện tích tam giác đều KMN là \(S = \frac{{M{N^2}\sqrt 3 }}{4} = \frac{{{{\left( {\frac{{8x}}{3}} \right)}^2}\sqrt 3 }}{4} = \frac{{16{x^2}\sqrt 3 }}{9}\).
Suy ra a = 16, b = 9.
Vậy P = a + b = 16 + 9 = 25.
Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu sau:

Hãy cho biết 75% học sinh khối 11 ngủ nhiều nhất bao nhiêu giờ?
Đáp án:
Đáp án:
Tìm tứ phân vị thứ ba.
Cỡ mẫu: n = 6 + 12 + 13 + 10 + 3 = 44.
Do \(\frac{{3n}}{4} = 33\) nên \({Q_3} = \frac{{{x_{33}} + {x_{34}}}}{2} \in [7;8)\).
\({Q_3} = 7 + \frac{{\frac{{3.44}}{4} - (6 + 12 + 13)}}{{10}}(8 - 7) = 7,2\).
Vậy 75% học sinh khối 11 ngủ nhiều nhất 7,2 giờ.
Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 6: Tổng quan và Hướng dẫn Ôn tập
Chào mừng các em học sinh lớp 11 đến với đề thi học kì 1 môn Toán chương trình Chân trời sáng tạo - Đề số 6 do tusach.vn biên soạn. Đề thi này được thiết kế để giúp các em ôn tập và đánh giá kiến thức đã học trong học kì 1, chuẩn bị tốt nhất cho kỳ thi sắp tới.
Cấu trúc đề thi
Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 6 bao gồm hai phần chính:
- Phần trắc nghiệm: Khoảng 20 câu hỏi, tập trung vào các kiến thức cơ bản và vận dụng.
- Phần tự luận: Khoảng 3-5 câu hỏi, yêu cầu học sinh trình bày chi tiết lời giải và lập luận logic.
Nội dung đề thi
Đề thi tập trung vào các chủ đề chính sau:
- Đại số: Hàm số bậc hai, phương trình và bất phương trình bậc hai, hệ phương trình.
- Hình học: Vectơ, tích vô hướng, ứng dụng của tích vô hướng, đường thẳng và mặt phẳng trong không gian.
- Phân tích tổ hợp: Hoán vị, chỉnh hợp, tổ hợp.
- Xác suất: Các khái niệm cơ bản về xác suất.
Hướng dẫn ôn tập hiệu quả
Để đạt kết quả tốt nhất trong kỳ thi học kì 1, các em nên:
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các công thức và định lý quan trọng.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
- Ôn tập theo chủ đề: Chia nhỏ nội dung ôn tập thành các chủ đề nhỏ để dễ dàng nắm bắt và ghi nhớ.
- Làm đề thi thử: Làm các đề thi thử để đánh giá năng lực và làm quen với áp lực thời gian.
- Xem lại đáp án và phân tích lỗi sai: Sau khi làm đề thi thử, hãy xem lại đáp án và phân tích kỹ các lỗi sai để rút kinh nghiệm.
Tải đề thi và đáp án
Các em có thể tải đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 6 và đáp án chi tiết ngay tại tusach.vn. Chúng tôi luôn cập nhật những đề thi mới nhất và chất lượng nhất để phục vụ nhu cầu học tập của các em.
Lợi ích khi sử dụng đề thi của tusach.vn
- Đề thi được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
- Đáp án chi tiết, dễ hiểu.
- Miễn phí tải về.
- Cập nhật thường xuyên.
Lời khuyên
Hãy sử dụng đề thi này như một công cụ hỗ trợ đắc lực trong quá trình ôn tập của mình. Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi sắp tới!
| Chủ đề | Mức độ quan trọng |
|---|---|
| Hàm số bậc hai | Cao |
| Tích vô hướng | Trung bình |
| Hoán vị, chỉnh hợp, tổ hợp | Trung bình |
| Nguồn: tusach.vn | |