Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 1
Tổng quan nội dung
Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 1
Chào mừng các em học sinh lớp 11 đến với đề thi học kì 1 môn Toán theo chương trình Chân trời sáng tạo - Đề số 1.
Đề thi này được biên soạn bám sát cấu trúc đề thi chính thức của Bộ Giáo dục và Đào tạo, giúp các em làm quen với dạng đề và rèn luyện kỹ năng giải quyết bài toán.
Tusach.vn hy vọng với đề thi này, các em sẽ có một kỳ thi học kì 1 thành công tốt đẹp!
Đề bài
Nếu một cung tròn có số đo là 20 độ thì số đo radian của nó là:
- A.\(\frac{\pi }{{10}}\).
- B.\(\frac{\pi }{9}\).
- C.\(\frac{\pi }{8}\).
- D.\(\frac{\pi }{{11}}\).
Chọn đáp án đúng
- A.\(\cos \left( {a + b} \right) = \cos a\cos b + \sin a\sin b\).
- B.\(\cos \left( {a + b} \right) = \cos a\sin b - \sin a\cos b\).
- C.\(\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b\).
- D.\(\cos \left( {a + b} \right) = \cos a\sin b + \sin a\cos b\).
Nghiệm của phương trình \(\sin x = \sin \frac{\pi }{3}\) là:
- A.\(\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
- B.\(\left[ \begin{array}{l}x = \frac{\pi }{3} + k\pi \\x = \frac{{2\pi }}{3} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
- C.\(x = \pm \frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
- D.\(x = \pm \frac{{2\pi }}{3} + k\pi \left( {k \in \mathbb{Z}} \right)\).
Tập xác định của D của hàm số \(y = \cot x\) là:
- A.\(D = \mathbb{R}\).
- B.\(D = \mathbb{R}\backslash \left\{ {\frac{{k\pi }}{2}\left| {k \in \mathbb{Z}} \right.} \right\}\).
- C.\(D = \mathbb{R}\backslash \left\{ {k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
- D.\(D = \mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
Hàm số \(y = \tan x\)tuần hoàn với chu kì là:
- A.\(\frac{\pi }{2}\).
- B.\(\pi \).
- C.\(\frac{{3\pi }}{2}\).
- D.\(2\pi \).
Độ dài của 60 lá dương xỉ trưởng thành được cho bằng mẫu số liệu ghép nhóm sau:

Tần số của nhóm [30;40) là:
- A.9.
- B.17.
- C.24.
- D.10.
Trong các dãy số sau, dãy số nào là dãy số tăng?
- A.1; 2; 3; 4; …
- B.4; 3; 2; 5; …
- C.1; 2; 1; 2; …
- D.4; 3; 1; 2; …
Trong các dãy số sau, dãy số nào là cấp số cộng?
- A.1; 2; 3; 5; 7; …
- B.1; 3; 5; 7; 9; ….
- C.1; 2; 4; 8; 16; ….
- D.1; 1; 2; 3; 4; ….
Dãy số nào dưới đây được viết dưới dạng công thức của số hạng tổng quát?
- A.1; 4; 7; 8; 10; ...
- B.Dãy số gồm các số nguyên dương chia hết cho 5.
- C.\({u_1} = 2;\;{u_n} = 3{u_{n - 1}} - 1\) với \(n \ge 2\).
- D.\({u_n} = \frac{1}{n}\left( {n \in \mathbb{N}*} \right)\).
Biết \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\). Chọn đáp án đúng
- A.\(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = + \infty \).
- B.\(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = - \infty \).
- C.\(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = 0\).
- D.\(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = a\).
Hàm số nào sau đây liên tục trên \(\mathbb{R}\)?
- A.\(y = \frac{{x + 1}}{x}\).
- B.\(y = \tan x\).
- C.\(y = \frac{{x + 1}}{{{x^2}}}\).
- D.\(y = \frac{{x - 1}}{{{x^2} + 1}}\).
Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } \frac{4}{n}\) bằng:
- A.1.
- B.0.
- C.2.
- D.4.
Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left( {x - 3} \right)\) là:
- A.1.
- B.2.
- C.\( - 2\).
- D.\( + \infty \).
Cho lăng trụ tam giác ABC.A’B’C’. Khẳng định nào sau đây là đúng?
- A.(ABC) // (AB’C’).
- B.(B’A’C’) // (B’AC).
- C.(ABC’) // (A’B’C’).
- D.(ABC) // (A’B’C’).
Cho đường thẳng d và mặt phẳng \(\left( \alpha \right)\) không có điểm chung. Kết luận nào sau đây là đúng?
- A.\(d//\left( \alpha \right)\).
- B.d cắt \(\left( \alpha \right)\).
- C.d nằm trong \(\left( \alpha \right)\).
- D.d cắt a hoặc d nằm trong \(\left( \alpha \right)\).
Cho hai đường thẳng a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
- A.1.
- B.2.
- C.4.
- D.3.
Hình chóp tứ giác có mặt bên là hình gì?
- A.Hình tứ giác.
- B.Hình tam giác.
- C.Hình ngũ giác.
- D.Hình lục giác.
Nếu d là giao tuyến của hai mặt phẳng phân biệt (P) và (Q) thì:
- A.\(d \subset \left( P \right)\).
- B.\(d \subset \left( Q \right)\).
- C.Cả a và b đều đúng.
- D.Cả a và b đều sai.
Cho tứ diện ABCD. Chọn đáp án đúng.
- A.AB và CD là hai đường thẳng vuông góc với nhau.
- B.AB và CD là hai đường thẳng cắt nhau.
- C.AB và CD là hai đường thẳng cùng thuộc một mặt phẳng.
- D.AB và CD là hai đường thẳng chéo nhau.
Khảo sát thời gian tập thể dục trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Giá trị đại diện của nhóm \(\left[ {60;80} \right)\) là:
- A.60.
- B.70.
- C.80.
- D.7.
Giá trị lớn nhất của hàm số \(y = 2\cos x + 1\) bằng:
- A.\( - 1\).
- B.1.
- C.3.
- D.\(\frac{1}{2}\).
Tìm tất cả các giá trị của m để phương trình \({\cos ^2}x - {\sin ^2}x - m = 0\) có nghiệm?
- A.\(m \ge 1\).
- B.\( - 1 \le m \le 1\).
- C.\(m \le 1\).
- D.\(m \ge 0\).
Cho góc \(\alpha \) thỏa mãn \(\sin \alpha = \frac{1}{2}\) và \(\frac{\pi }{2} < \alpha < \pi \). Tính \(\cos \alpha \).
- A.\(\cos \alpha = \frac{{ - \sqrt 3 }}{2}\).
- B.\(\cos \alpha = \frac{{\sqrt 3 }}{2}\).
- C.\(\cos \alpha = \frac{{ \pm \sqrt 3 }}{2}\).
- D.Cả A, B, C đều sai.
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + 2{u_{n - 2}}\end{array} \right.\left( {n \ge 3,n \in \mathbb{N}} \right)\). Giá trị của \({u_3} + {u_4}\) là:
- A.4.
- B.6.
- C.8.
- D.10.
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2,q = 3\). Tính tổng của mười số hạng đầu tiên của cấp số nhân đó.
- A.59048.
- B.59084.
- C.59050.
- D.59080.
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2;d = 3\). Khi đó, \({u_4} + {u_6}\) bằng:
- A.24.
- B.30.
- C.26.
- D.28.
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 16}}{{x - 2}}\) là:
- A.2.
- B.0.
- C.\( - \infty \).
- D.\( + \infty \).
Biết rằng \(\mathop {\lim }\limits_{x \to \sqrt 3 } \frac{{{x^2} - 3}}{{x - \sqrt 3 }} = a\sqrt b \) (với a, b là các số nguyên). Chọn đáp án đúng:
- A.\({a^2} + {b^2} = 13\).
- B.\({a^2} + {b^2} = 9\).
- C.\({a^2} + {b^2} = 6\).
- D.\({a^2} + {b^2} = 11\).
Với giá trị nào của m thì hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 1\;khi\;x \ne -1\\m\;\;\;\;\;\;\,khi\;x = -1\end{array} \right.\) liên tục tại \({x_0} = - 1\)?
- A.\(m = 2\).
- B.\(m = - 2\).
- C.\(m = 1\).
- D.\(m = - 1\).
Cho tam giác ABC và một điểm S không thuộc mặt phẳng ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Khi đó, giao tuyến của hai mặt phẳng (SBN) và (SCM) là:
- A.SG với G là giao điểm của BN và MC.
- B.SN.
- C.SM.
- D.AG với G là giao điểm của BN và MC.
Cho 4 điểm phân biệt A, B, C, D trong đó không có ba điểm nào thẳng hàng. Xác định được tất cả bao nhiêu từ 3 trong 4 điểm đã cho?
- A.1.
- B.2.
- C.3.
- D.4.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là:
- A.Đường thẳng m qua S vuông góc với AB.
- B.Đường thẳng m qua S song song với AB.
- C.SO với O là giao điểm của AC và BD.
- D.Cả A, B, C đều sai.
Cho hình hộp ABCD. A’B’C’D’ có AC cắt BD tại O và A’C’ cắt B’D’ tại O’. Khi đó, mặt phẳng (AB’D’) song song với mặt phẳng nào dưới đây?
- A.(A’OC’).
- B.(BDA’).
- C.(BDC’).
- D.(BCD).
Tìm cân nặng trung bình của học sinh lớp 11A cho dưới mẫu số liệu ghép nhóm sau:

- A.52,33.
- B.50,33.
- C.55,33.
- D.51,33.
Tuổi thọ (năm) của các bình ác quy ô tô được cho như sau:

Cỡ mẫu của mẫu số liệu ghép nhóm trên là:
- A.15.
- B.56.
- C.10.
- D.7.
Tính giới hạn sau: \(I = \mathop {\lim }\limits_{x \to 1} \frac{{2\sqrt {3 + x} - 4x}}{{2x - 2}}\)
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. M là điểm nằm trên cạnh BC sao cho \(MB = 2MC\). Chứng minh rằng MG // (ACD).
Cho hai số thực a và b thỏa mãn điều kiện \(\sin \left( {a + b} \right) - 2\cos \left( {a - b} \right) = 0\). Tính giá trị của biểu thức \(A = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}}\).
Chứng minh rằng dãy số \({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \ldots + \frac{1}{{n(n + 1)}}\) tăng và bị chặn trên.
Lời giải và đáp án
Nếu một cung tròn có số đo là 20 độ thì số đo radian của nó là:
- A.\(\frac{\pi }{{10}}\).
- B.\(\frac{\pi }{9}\).
- C.\(\frac{\pi }{8}\).
- D.\(\frac{\pi }{{11}}\).
Đáp án : B
Sử dụng công thức: \({\alpha ^0} = \alpha .\frac{\pi }{{180}}rad\).
Ta có: \({20^0} = 20.\frac{\pi }{{180}} = \frac{\pi }{9}\)
Chọn đáp án đúng
- A.\(\cos \left( {a + b} \right) = \cos a\cos b + \sin a\sin b\).
- B.\(\cos \left( {a + b} \right) = \cos a\sin b - \sin a\cos b\).
- C.\(\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b\).
- D.\(\cos \left( {a + b} \right) = \cos a\sin b + \sin a\cos b\).
Đáp án : C
Sử dụng công thức: \(\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b\).
Ta có:\(\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b\)
Nghiệm của phương trình \(\sin x = \sin \frac{\pi }{3}\) là:
- A.\(\left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
- B.\(\left[ \begin{array}{l}x = \frac{\pi }{3} + k\pi \\x = \frac{{2\pi }}{3} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\).
- C.\(x = \pm \frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)\).
- D.\(x = \pm \frac{{2\pi }}{3} + k\pi \left( {k \in \mathbb{Z}} \right)\).
Đáp án : A
Phương trình \(\sin x = \sin \alpha \)có nghiệm: \(x = \alpha + k2\pi ,k \in \mathbb{Z}\) và \(x = \pi - \alpha + k2\pi ,k \in \mathbb{Z}\)
\(\sin x = \sin \frac{\pi }{3} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \pi - \frac{\pi }{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Tập xác định của D của hàm số \(y = \cot x\) là:
- A.\(D = \mathbb{R}\).
- B.\(D = \mathbb{R}\backslash \left\{ {\frac{{k\pi }}{2}\left| {k \in \mathbb{Z}} \right.} \right\}\).
- C.\(D = \mathbb{R}\backslash \left\{ {k2\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
- D.\(D = \mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\).
Đáp án : D
Sử dụng kiến thức về tập xác định của hàm số lượng giác: Hàm số \(y = \cot x\) có tập xác định là \(D = \mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\)
Hàm số \(y = \cot x\) có tập xác định là \(D = \mathbb{R}\backslash \left\{ {k\pi \left| {k \in \mathbb{Z}} \right.} \right\}\)
Hàm số \(y = \tan x\)tuần hoàn với chu kì là:
- A.\(\frac{\pi }{2}\).
- B.\(\pi \).
- C.\(\frac{{3\pi }}{2}\).
- D.\(2\pi \).
Đáp án : B
Sử dụng kiến thức về đồ thị và tính chất của hàm số \(y = \tan x\): Hàm số \(y = \tan x\) tuần hoàn với chu kì \(\pi \)
Hàm số \(y = \tan x\) tuần hoàn với chu kì \(\pi \)
Độ dài của 60 lá dương xỉ trưởng thành được cho bằng mẫu số liệu ghép nhóm sau:

Tần số của nhóm [30;40) là:
- A.9.
- B.17.
- C.24.
- D.10.
Đáp án : C
Sử dụng kiến thức về tần số của mẫu số liệu ghép nhóm: Số giá trị của mẫu số liệu thuộc mỗi nhóm là tần số của nhóm đó.
Tần số của nhóm \(\left[ {30;40} \right)\) là 24.
Trong các dãy số sau, dãy số nào là dãy số tăng?
- A.1; 2; 3; 4; …
- B.4; 3; 2; 5; …
- C.1; 2; 1; 2; …
- D.4; 3; 1; 2; …
Đáp án : A
Sử dụng kiến thức về dãy số tăng: Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số tăng nếu ta có: \({u_{n + 1}} > {u_n}\) với mọi \(n \in \mathbb{N}*\)
Trong các dãy số trên, chỉ có dãy số 1; 2; 3; 4; … có \(1 < 2 < 3 < 4...\) nên dãy số 1; 2; 3; 4; … là dãy số tăng.
Trong các dãy số sau, dãy số nào là cấp số cộng?
- A.1; 2; 3; 5; 7; …
- B.1; 3; 5; 7; 9; ….
- C.1; 2; 4; 8; 16; ….
- D.1; 1; 2; 3; 4; ….
Đáp án : B
Sử dụng kiến thức về cấp số cộng: Cấp số cộng là một dãy số (hữu hạn hay vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Trong các dãy số trên, chỉ có dãy số 1; 3; 5; 7; 9; … có kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d \(\left( {d = 2} \right)\)
Dãy số nào dưới đây được viết dưới dạng công thức của số hạng tổng quát?
- A.1; 4; 7; 8; 10; ...
- B.Dãy số gồm các số nguyên dương chia hết cho 5.
- C.\({u_1} = 2;\;{u_n} = 3{u_{n - 1}} - 1\) với \(n \ge 2\).
- D.\({u_n} = \frac{1}{n}\left( {n \in \mathbb{N}*} \right)\).
Đáp án : D
Sử dụng kiến thức về cách cho một dãy số.
Dãy số được viết dưới dạng công thức của số hạng tổng quát là: \({u_n} = \frac{1}{n}\left( {n \in \mathbb{N}*} \right)\)
Biết \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\). Chọn đáp án đúng
- A.\(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = + \infty \).
- B.\(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = - \infty \).
- C.\(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = 0\).
- D.\(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = a\).
Đáp án : A
Sử dụng quy tắc về giới hạn vô cực của dãy số: Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = + \infty \).
Nếu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty ,\mathop {\lim }\limits_{n \to + \infty } {v_n} = a > 0\) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n}{v_n} = + \infty \).
Hàm số nào sau đây liên tục trên \(\mathbb{R}\)?
- A.\(y = \frac{{x + 1}}{x}\).
- B.\(y = \tan x\).
- C.\(y = \frac{{x + 1}}{{{x^2}}}\).
- D.\(y = \frac{{x - 1}}{{{x^2} + 1}}\).
Đáp án : D
Sử dụng kiến thức về hàm số liên tục trên một khoảng: Hàm số \(y = f\left( x \right)\) được gọi là liên tục trên khoảng (a; b) nếu nó liên tục tại mọi điểm trên khoảng này.
Hàm số \(y = \frac{{x - 1}}{{{x^2} + 1}}\) liên tục trên \(\mathbb{R}\)
Giá trị của \(\mathop {\lim }\limits_{n \to + \infty } \frac{4}{n}\) bằng:
- A.1.
- B.0.
- C.2.
- D.4.
Đáp án : B
Sử dụng công thức: \(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} = 0\)
Ta có: \(\mathop {\lim }\limits_{n \to + \infty } \frac{1}{n} = 0\) nên \(\mathop {\lim }\limits_{n \to + \infty } \frac{4}{n} = 0\)
Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left( {x - 3} \right)\) là:
- A.1.
- B.2.
- C.\( - 2\).
- D.\( + \infty \).
Đáp án : C
Sử dụng quy tắc tính giới hạn của hàm số tại một điểm: Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L,\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\) thì \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) - g\left( x \right)} \right] = L - M\)
\(\mathop {\lim }\limits_{x \to 1} \left( {x - 3} \right) = 1 - 3 = - 2\)
Cho lăng trụ tam giác ABC.A’B’C’. Khẳng định nào sau đây là đúng?
- A.(ABC) // (AB’C’).
- B.(B’A’C’) // (B’AC).
- C.(ABC’) // (A’B’C’).
- D.(ABC) // (A’B’C’).
Đáp án : D
Sử dụng kiến thức về hình lăng trụ tam giác: Hình lăng trụ có hai đáy song song với nhau.
Hình lăng trụ tam giác ABC.A’B’C’ có (ABC) // (A’B’C’).
Cho đường thẳng d và mặt phẳng \(\left( \alpha \right)\) không có điểm chung. Kết luận nào sau đây là đúng?
- A.\(d//\left( \alpha \right)\).
- B.d cắt \(\left( \alpha \right)\).
- C.d nằm trong \(\left( \alpha \right)\).
- D.d cắt a hoặc d nằm trong \(\left( \alpha \right)\).
Đáp án : A
Sử dụng kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng: Nếu d và \(\left( \alpha \right)\) không có điểm chung thì \(d//\left( \alpha \right)\)
Nếu d và \(\left( \alpha \right)\) không có điểm chung thì \(d//\left( \alpha \right)\)
Cho hai đường thẳng a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
- A.1.
- B.2.
- C.4.
- D.3.
Đáp án : C
Sử dụng kiến thức về vị trí tương đối của hai đường thẳng: Có bốn vị trí tương đối của hai đường thẳng a và b trong không gian: cắt nhau, trùng nhau, song song và chéo nhau.
Hai đường thẳng a và b có thể: cắt nhau, trùng nhau, song song, chéo nhau.
Hình chóp tứ giác có mặt bên là hình gì?
- A.Hình tứ giác.
- B.Hình tam giác.
- C.Hình ngũ giác.
- D.Hình lục giác.
Đáp án : B
Sử dụng kiến thức về hình chóp: Hình chóp tứ giác có mặt bên là hình tam giác.
Hình chóp tứ giác có mặt bên là hình tam giác.
Nếu d là giao tuyến của hai mặt phẳng phân biệt (P) và (Q) thì:
- A.\(d \subset \left( P \right)\).
- B.\(d \subset \left( Q \right)\).
- C.Cả a và b đều đúng.
- D.Cả a và b đều sai.
Đáp án : C
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng chung d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó.
Vì d là giao tuyến của hai mặt phẳng phân biệt (P) và (Q) thì \(d \subset \left( P \right)\) và \(d \subset \left( Q \right)\)
Cho tứ diện ABCD. Chọn đáp án đúng.
- A.AB và CD là hai đường thẳng vuông góc với nhau.
- B.AB và CD là hai đường thẳng cắt nhau.
- C.AB và CD là hai đường thẳng cùng thuộc một mặt phẳng.
- D.AB và CD là hai đường thẳng chéo nhau.
Đáp án : D
Sử dụng kiến thức về hai đường thẳng chéo nhau: Nếu hai đường thẳng a và b không cùng nằm trong bất kì một mặt phẳng nào thì ta nó a và b chéo nhau.
Vì hai đường thẳng AB và CD không cùng nằm trong một mặt phẳng nào nên AB và CD là hai đường thẳng chéo nhau.
Khảo sát thời gian tập thể dục trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Giá trị đại diện của nhóm \(\left[ {60;80} \right)\) là:
- A.60.
- B.70.
- C.80.
- D.7.
Đáp án : B
Sử dụng kiến thức về giá trị đại diện của một nhóm.
Cho mẫu số liệu ghép nhóm:

Với nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\) thì \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\).
Giá trị đại diện của nhóm \(\left[ {60;80} \right)\) là: \(\frac{{60 + 80}}{2} = 70\).
Giá trị lớn nhất của hàm số \(y = 2\cos x + 1\) bằng:
- A.\( - 1\).
- B.1.
- C.3.
- D.\(\frac{1}{2}\).
Đáp án : C
Sử dụng kiến thức về hàm số lượng giác: \( - 1 \le \cos x \le 1\) với mọi số thực x.
Vì \(\cos x \le 1\;\forall x \in \mathbb{R} \Rightarrow 2\cos x \le 2\;\forall x \in \mathbb{R} \Rightarrow 2\cos x + 1 \le 3\;\forall x \in \mathbb{R}\)
Do đó, giá trị lớn nhất của hàm số \(y = 2\cos x + 1\) là 3
Tìm tất cả các giá trị của m để phương trình \({\cos ^2}x - {\sin ^2}x - m = 0\) có nghiệm?
- A.\(m \ge 1\).
- B.\( - 1 \le m \le 1\).
- C.\(m \le 1\).
- D.\(m \ge 0\).
Đáp án : B
Sử dụng kiến thức về điều kiện có nghiệm của phương trình \(\cos x = m\): Phương trình \(\cos x = m\) có nghiệm khi và chỉ khi \(\left| m \right| \le 1\)
Ta có: \({\cos ^2}x - {\sin ^2}x - m = 0 \Leftrightarrow \cos 2x = m\left( 1 \right)\)
Để phương trình (1) có nghiệm thì \(\left| m \right| \le 1 \Leftrightarrow - 1 \le m \le 1\)
Cho góc \(\alpha \) thỏa mãn \(\sin \alpha = \frac{1}{2}\) và \(\frac{\pi }{2} < \alpha < \pi \). Tính \(\cos \alpha \).
- A.\(\cos \alpha = \frac{{ - \sqrt 3 }}{2}\).
- B.\(\cos \alpha = \frac{{\sqrt 3 }}{2}\).
- C.\(\cos \alpha = \frac{{ \pm \sqrt 3 }}{2}\).
- D.Cả A, B, C đều sai.
Đáp án : A
Sử dụng công thức: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = \pm \sqrt {1 - {{\sin }^2}\alpha } = \pm \frac{{\sqrt 3 }}{2}\).
Mà \(\frac{\pi }{2} < \alpha < \pi \) nên điểm cuối của \(\alpha\) thuộc góc phần tư thứ II, suy ra \(\cos \alpha < 0\). Do đó, \(\cos \alpha = \frac{{ - \sqrt 3 }}{2}\).
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + 2{u_{n - 2}}\end{array} \right.\left( {n \ge 3,n \in \mathbb{N}} \right)\). Giá trị của \({u_3} + {u_4}\) là:
- A.4.
- B.6.
- C.8.
- D.10.
Đáp án : C
Tính các giá trị \({u_3}\) và \({u_4}\) rồi tính tổng.
Ta có: \({u_3} = {u_2} + 2{u_1} = 1 + 2.1 = 3;{u_4} = {u_3} + 2{u_2} = 3 + 2.1 = 5\). Do đó, \({u_3} + {u_4} = 3 + 5 = 8\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2,q = 3\). Tính tổng của mười số hạng đầu tiên của cấp số nhân đó.
- A.59048.
- B.59084.
- C.59050.
- D.59080.
Đáp án : A
Sử dụng kiến thức về tổng của n số hạng đầu của một cấp số nhân: Cho cấp số nhân \(\left( {{u_n}} \right)\) với công bội \(q \ne 1\). Khi đó, tổng của n số hạng đầu tiên trong cấp số nhân là: \({S_n} = \frac{{{u_1}\left( {1 - {q^n}} \right)}}{{1 - q}}\)
Tổng của 10 số hạng đầu tiên của cấp số nhân là: \(S = \frac{{2.\left( {1 - {3^{10}}} \right)}}{{1 - 3}} = 59048\)
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 2;d = 3\). Khi đó, \({u_4} + {u_6}\) bằng:
- A.24.
- B.30.
- C.26.
- D.28.
Đáp án : D
Sử dụng kiến thức về công thức số hạng tổng quát của cấp số cộng: Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\) của nó được xác định theo công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d\).
Ta có: \({u_4} = {u_1} + 3d = 2 + 3.3 = 11;{u_6} = {u_1} + 5d = 2 + 5.3 = 17\)
Do đó, \({u_4} + {u_6} = 11 + 17 = 28\)
Kết quả của giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 16}}{{x - 2}}\) là:
- A.2.
- B.0.
- C.\( - \infty \).
- D.\( + \infty \).
Đáp án : C
Sử dụng kiến thức tính giới hạn của thương \(\frac{{f\left( x \right)}}{{g\left( x \right)}}\): Nếu \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L < 0\), \(\mathop {\lim }\limits_{x \to x_0^ + } g\left( x \right) = 0\) và \(g\left( x \right) > 0\) thì \(\mathop {\lim }\limits_{x \to x_0^ + } \frac{{f\left( x \right)}}{{g\left( x \right)}} = - \infty \)
Ta có: \(\mathop {\lim }\limits_{x \to {2^ + }} \left( {x - 16} \right) = 2 - 16 = - 14 < 0,\mathop {\lim }\limits_{x \to {2^ + }} \left( {x - 2} \right) = 0\)
Với \(x \to {2^ + }\) thì \(x > 2\) nên \(x - 2 > 0\). Do đó, \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 16}}{{x - 2}} = - \infty \)
Biết rằng \(\mathop {\lim }\limits_{x \to \sqrt 3 } \frac{{{x^2} - 3}}{{x - \sqrt 3 }} = a\sqrt b \) (với a, b là các số nguyên). Chọn đáp án đúng:
- A.\({a^2} + {b^2} = 13\).
- B.\({a^2} + {b^2} = 9\).
- C.\({a^2} + {b^2} = 6\).
- D.\({a^2} + {b^2} = 11\).
Đáp án : A
Sử dụng kiến thức về giới hạn hàm số để làm: Nhận thấy \(x = \sqrt 3 \) là nghiệm của cả tử thức và mẫu thức nên ta cần rút phân thức trước khi tính giới hạn.
Ta có: \(\mathop {\lim }\limits_{x \to \sqrt 3 } \frac{{{x^2} - 3}}{{x - \sqrt 3 }} = \mathop {\lim }\limits_{x \to \sqrt 3 } \frac{{\left( {x - \sqrt 3 } \right)\left( {x + \sqrt 3 } \right)}}{{x - \sqrt 3 }} = \mathop {\lim }\limits_{x \to \sqrt 3 } \left( {x + \sqrt 3 } \right) = \sqrt 3 + \sqrt 3 = 2\sqrt 3 \).
Do đó, \(a = 2,b = 3\). Suy ra: \({a^2} + {b^2} = {2^2} + {3^2} = 13\).
Với giá trị nào của m thì hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 1\;khi\;x \ne -1\\m\;\;\;\;\;\;\,khi\;x = -1\end{array} \right.\) liên tục tại \({x_0} = - 1\)?
- A.\(m = 2\).
- B.\(m = - 2\).
- C.\(m = 1\).
- D.\(m = - 1\).
Đáp án : D
Sử dụng kiến thức về hàm số liên tục: Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng (a; b) chứa điểm \({x_0}\). Hàm số \(f\left( x \right)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Tập xác định của hàm số f(x) là \(D = \mathbb{R}\).
Ta có: \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \left( {2x + 1} \right) = - 1\).
Hàm số đã cho liên tục tại \({x_0} = - 1\) khi \(f\left( { - 1} \right) = \mathop {\lim }\limits_{x \to - 1} f\left( x \right) \Leftrightarrow m = - 1\).
Cho tam giác ABC và một điểm S không thuộc mặt phẳng ABC. Gọi M, N lần lượt là trung điểm của AB và AC. Khi đó, giao tuyến của hai mặt phẳng (SBN) và (SCM) là:
- A.SG với G là giao điểm của BN và MC.
- B.SN.
- C.SM.
- D.AG với G là giao điểm của BN và MC.
Đáp án : A
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Đường thẳng chung d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó.
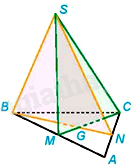
Xét mặt phẳng (ABC), gọi G là giao điểm của BN và CM.
Vì \(G \in BN \Rightarrow G \in \left( {SBN} \right);G \in CM \Rightarrow G \in \left( {SCM} \right)\) nên G là điểm chung của hai mặt phẳng (SBN) và (SCM)
Ta có: \(S \in SB \Rightarrow S \in \left( {SBN} \right),S \in SC \Rightarrow S \in \left( {SCM} \right)\) nên S là điểm chung của hai mặt phẳng (SBN) và (SCM)
Do đó, SG là giao tuyến của hai mặt phẳng (SBN) và (SCM).
Cho 4 điểm phân biệt A, B, C, D trong đó không có ba điểm nào thẳng hàng. Xác định được tất cả bao nhiêu từ 3 trong 4 điểm đã cho?
- A.1.
- B.2.
- C.3.
- D.4.
Đáp án : D
Sử dụng kiến thức về cách xác định một mặt phẳng: Một mặt phẳng hoàn toàn được xác định qua ba điểm không thẳng hàng.
Ta xác định được các mặt phẳng (ABC), (ABD), (ACD), (BCD). Do đó, xác định được 4 mặt phẳng.
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là:
- A.Đường thẳng m qua S vuông góc với AB.
- B.Đường thẳng m qua S song song với AB.
- C.SO với O là giao điểm của AC và BD.
- D.Cả A, B, C đều sai.
Đáp án : B
Sử dụng kiến thức về giao tuyến của hai mặt phẳng: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
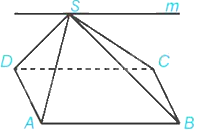
Ta có: Vì ABCD là hình bình hành nên AB // CD. Mà \(AB \subset \left( {SAB} \right),CD \subset \left( {SCD} \right)\)
Do đó, giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng m qua S song song với AB.
Cho hình hộp ABCD. A’B’C’D’ có AC cắt BD tại O và A’C’ cắt B’D’ tại O’. Khi đó, mặt phẳng (AB’D’) song song với mặt phẳng nào dưới đây?
- A.(A’OC’).
- B.(BDA’).
- C.(BDC’).
- D.(BCD).
Đáp án : C
Sử dụng kiến thức về hai mặt phẳng song song: Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng (Q) thì (P) và (Q) song song với nhau.
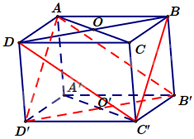
Vì BD // B’D’ nên B’D’ // (BDC’). Vì AD’ // BC’ nên AD’ // (BDC’)
Lại có hai đường thẳng AD’ và B’D’ cắt nhau và nằm trong mặt phẳng (AB’D’). Do đó, (AB’D’) // (BDC’)
Tìm cân nặng trung bình của học sinh lớp 11A cho dưới mẫu số liệu ghép nhóm sau:

- A.52,33.
- B.50,33.
- C.55,33.
- D.51,33.
Đáp án : D
Sử dụng kiến thức số trung bình của mẫu số liệu ghép nhóm:
Cho mẫu số liệu ghép nhóm

Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\overline x \): \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\), trong đó \(n = {m_1} + ... + {m_k}\) là cỡ mẫu và \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) (với \(i = 1;...;k\)) là giá trị đại diện của nhóm \(\left[ {{a_i};{a_{i + 1}}} \right)\).
Trong mỗi khoảng cân nặng, giá trị đại diện được thể hiện ở bảng sau:

Cân nặng trung bình của học sinh lớp 11A là: \(\overline x = \frac{{10.43 + 48.8 + 53.16 + 58.4 + 63.2 + 68.2}}{{10 + 8 + 16 + 4 + 2 + 2}} \approx 51,33\left( {kg} \right)\)
Tuổi thọ (năm) của các bình ác quy ô tô được cho như sau:

Cỡ mẫu của mẫu số liệu ghép nhóm trên là:
- A.15.
- B.56.
- C.10.
- D.7.
Đáp án : B
Sử dụng kiến thức về cỡ mẫu số liệu ghép nhóm: Cho mẫu số liệu ghép nhóm

Số trung bình của mẫu số liệu ghép nhóm là \(\overline x \): \(\overline x = \frac{{{m_1}{x_1} + ... + {m_k}{x_k}}}{n}\), trong đó \(n = {m_1} + ... + {m_k}\) là cỡ mẫu
Cỡ mẫu của mẫu số liệu ghép nhóm là: \(4 + 10 + 15 + 14 + 7 + 6 = 56\)
Tính giới hạn sau: \(I = \mathop {\lim }\limits_{x \to 1} \frac{{2\sqrt {3 + x} - 4x}}{{2x - 2}}\)
Sử dụng kiến thức về giới hạn của hàm số: Rút gọn biểu thức \(\frac{{2\sqrt {3 + x} - 4x}}{{2x - 2}}\) rồi áp dụng quy tắc về giới hạn để tính.
\(I = \mathop {\lim }\limits_{x \to 1} \frac{{2\sqrt {3 + x} - 4x}}{{2x - 2}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {2\sqrt {3 + x} - 4x} \right)\left( {2\sqrt {3 + x} + 4x} \right)}}{{2\left( {x - 1} \right)\left( {2\sqrt {3 + x} + 4x} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{4\left( {x + 3} \right) - 16{x^2}}}{{2\left( {x - 1} \right)\left( {2\sqrt {3 + x} + 4x} \right)}}\)
\( = \mathop {\lim }\limits_{x \to 1} \frac{{ - 16{x^2} + 4x + 12}}{{2\left( {x - 1} \right)\left( {2\sqrt {3 + x} + 4x} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - 4\left( {x - 1} \right)\left( {4x + 3} \right)}}{{4\left( {x - 1} \right)\left( {\sqrt {3 + x} + 2x} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - \left( {4x + 3} \right)}}{{\sqrt {3 + x} + 2x}} = \frac{{ - 7}}{4}\)
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD. M là điểm nằm trên cạnh BC sao cho \(MB = 2MC\). Chứng minh rằng MG // (ACD).
Sử dụng kiến thức về đường thẳng song song với mặt phẳng: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).
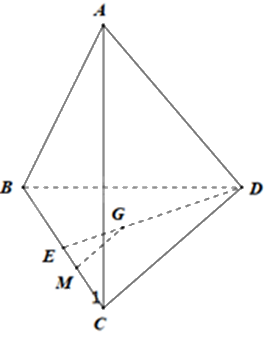
Gọi E là trung điểm của BC. Vì G là trọng tâm của tam giác BCD nên \(\frac{{GD}}{{ED}} = \frac{2}{3}\)
Mà \(MB = 2MC \Rightarrow 3MC = BC\). Lại có: \(EC = BE = \frac{1}{2}BC \Rightarrow \frac{{MC}}{{EC}} = \frac{2}{3}\)
Tam giác EDC có: \(\frac{{GD}}{{ED}} = \frac{{MC}}{{EC}}\left( { = \frac{2}{3}} \right)\) nên MG // CD (định lý Thalès đảo)
Mà \(CD \subset \left( {ACD} \right)\) nên MG // (ACD)
Cho hai số thực a và b thỏa mãn điều kiện \(\sin \left( {a + b} \right) - 2\cos \left( {a - b} \right) = 0\). Tính giá trị của biểu thức \(A = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}}\).
Sử dụng công thức: \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2};\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\)
\(A = \frac{1}{{2 - \sin 2a}} + \frac{1}{{2 - \sin 2b}} = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{\left( {2 - \sin 2a} \right)\left( {2 - \sin 2b} \right)}} = \frac{{4 - \left( {\sin 2a + \sin 2b} \right)}}{{4 - 2\left( {\sin 2a + \sin 2b} \right) + \sin 2a.\sin 2b}}\)
Vì \(\sin \left( {a + b} \right) - 2\cos \left( {a - b} \right) = 0 \Rightarrow \sin \left( {a + b} \right) = 2\cos \left( {a - b} \right)\)
Ta có: \(4 - \left( {\sin 2a + \sin 2b} \right) = 4 - 2\sin \left( {a + b} \right)\cos \left( {a - b} \right) = 4 - 4{\cos ^2}\left( {a - b} \right) = 4{\sin ^2}\left( {a - b} \right)\)
Lại có: \(4 - 2\left( {\sin 2a + \sin 2b} \right) + \sin 2a.\sin 2b\)
\( = 4 - 4\sin \left( {a + b} \right)\cos \left( {a - b} \right) + \frac{1}{2}\left[ {\cos \left( {2a - 2b} \right) - \cos \left( {2a + 2b} \right)} \right]\)
\( = 4 - 8{\cos ^2}\left( {a - b} \right) + \frac{1}{2}\left[ {2{{\cos }^2}\left( {a - b} \right) - 1 - 1 + 2{{\sin }^2}\left( {a + b} \right)} \right]\)
\( = 3 - 7{\cos ^2}\left( {a - b} \right) + {\sin ^2}\left( {a + b} \right) = 3 - 3{\cos ^2}\left( {a - b} \right) = 3{\sin ^2}\left( {a - b} \right)\)
Vậy \(A = \frac{{4{{\sin }^2}\left( {a - b} \right)}}{{3{{\sin }^2}\left( {a - b} \right)}} = \frac{4}{3}\)
Chứng minh rằng dãy số \({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \ldots + \frac{1}{{n(n + 1)}}\) tăng và bị chặn trên.
Sử dụng kiến thức về dãy số tăng: Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số tăng nếu \({u_{n + 1}} > {u_n}\) với mọi \(n \in \mathbb{N}*\)
Sử dụng kiến thức về dãy số bị chặn trên: Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn trên nếu tồn tại một số M sao cho \({u_n} \le M\) với mọi \(n \in \mathbb{N}*\).
Ta có: \({u_n} = \frac{{2 - 1}}{{1.2}} + \frac{{3 - 2}}{{2.3}} + \frac{{4 - 3}}{{3.4}} + \ldots + \frac{{(n + 1) - n}}{{n(n + 1)}} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \ldots + \frac{1}{n} - \frac{1}{{n + 1}} = 1 - \frac{1}{{n + 1}}\)
Xét hiệu: \({u_{n + 1}} - {u_n} = 1 - \frac{1}{{n + 2}} - \left( {1 - \frac{1}{{n + 1}}} \right) = \frac{1}{{n + 1}} - \frac{1}{{n + 2}} > 0 \Rightarrow \left( {{u_n}} \right)\) tăng
Nhận thấy \({u_n} = 1 - \frac{1}{{n + 1}} < 1 \Rightarrow \left( {{u_n}} \right)\) bị chặn trên.
Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 1: Tổng quan và Hướng dẫn
Kỳ thi học kì 1 môn Toán lớp 11 là một bước quan trọng để đánh giá kiến thức và kỹ năng của học sinh sau một học kỳ học tập. Đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 1 do Tusach.vn cung cấp là một công cụ hữu ích giúp học sinh ôn tập và làm quen với cấu trúc đề thi thực tế.
Cấu trúc đề thi
Đề thi này bao gồm các dạng câu hỏi trắc nghiệm và tự luận, tập trung vào các chủ đề chính sau:
- Đại số: Hàm số bậc hai, phương trình và bất phương trình bậc hai, dãy số, cấp số cộng và cấp số nhân.
- Hình học: Vectơ, tích vô hướng của hai vectơ, ứng dụng của tích vô hướng, đường thẳng trong mặt phẳng.
Tại sao nên luyện tập với đề thi này?
- Làm quen với cấu trúc đề thi: Đề thi được thiết kế theo cấu trúc đề thi chính thức, giúp học sinh làm quen với dạng đề và phân bổ thời gian hợp lý.
- Rèn luyện kỹ năng giải quyết bài toán: Đề thi chứa nhiều dạng bài tập khác nhau, giúp học sinh rèn luyện kỹ năng giải quyết bài toán một cách linh hoạt và hiệu quả.
- Đánh giá năng lực bản thân: Sau khi làm đề thi, học sinh có thể tự đánh giá năng lực bản thân và xác định những kiến thức còn yếu để tập trung ôn tập.
- Đáp án chi tiết: Tusach.vn cung cấp đáp án chi tiết cho từng câu hỏi, giúp học sinh hiểu rõ phương pháp giải và tự kiểm tra kết quả.
Hướng dẫn ôn tập hiệu quả
Để đạt kết quả tốt nhất trong kỳ thi học kì 1, học sinh nên:
- Nắm vững kiến thức cơ bản: Đảm bảo hiểu rõ các định nghĩa, định lý và công thức quan trọng trong chương trình học.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
- Sử dụng các tài liệu ôn tập: Tham khảo sách giáo khoa, sách bài tập, đề thi thử và các tài liệu ôn tập khác để bổ sung kiến thức và kỹ năng.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn trong quá trình học tập, hãy tìm kiếm sự giúp đỡ từ giáo viên, bạn bè hoặc các trung tâm gia sư.
Tải đề thi và đáp án
Các em có thể tải đề thi học kì 1 Toán 11 Chân trời sáng tạo - Đề số 1 và đáp án chi tiết ngay tại Tusach.vn. Chúc các em ôn tập tốt và đạt kết quả cao trong kỳ thi sắp tới!
Bảng so sánh các chương trình Toán 11
| Chương trình | Nhà xuất bản | Đặc điểm |
|---|---|---|
| Chân trời sáng tạo | Giáo dục Việt Nam | Tiếp cận theo năng lực, chú trọng phát triển tư duy. |
| Kết nối tri thức với cuộc sống | Giáo dục Việt Nam | Liên hệ thực tế, ứng dụng kiến thức vào cuộc sống. |
Tusach.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục tri thức. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích khác!