Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 4
Tổng quan nội dung
Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 4
Tusach.vn xin giới thiệu Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 4, được biên soạn bám sát chương trình học và cấu trúc đề thi chính thức. Đề thi này là tài liệu ôn tập lý tưởng giúp học sinh làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các câu hỏi trắc nghiệm và tự luận, tập trung vào các chủ đề quan trọng trong chương trình học kì 1. Đi kèm với đề thi là đáp án chi tiết, giúp học sinh tự đánh giá kết quả và tìm ra những điểm cần cải thiện.
Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay \(3\frac{2}{5}\) vòng ngược chiều kim đồng hồ?
Đề bài
Phần trắc nghiệm (5 điểm)
Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay \(3\frac{2}{5}\) vòng ngược chiều kim đồng hồ?
A. \(1\;{224^0}\) | B. \(\frac{{34\pi }}{5}rad\) |
C. Cả A và B đều đúng | D. Cả A và B đều sai. |
Câu 2: Chọn đáp án đúng:
A. \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = \frac{1}{2}\tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\) B. \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = 2\tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\) |
C. \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = \tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\) D. \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = 3\tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\) |
Câu 3: Chọn khẳng định đúng:
A. \({\sin ^4}\alpha - {\cos ^4}\alpha = \cos 2\alpha \) | B. \({\sin ^4}\alpha - {\cos ^4}\alpha = - \cos 2\alpha \) |
C. \({\sin ^4}\alpha - {\cos ^4}\alpha = \sin 2\alpha \) | D. \({\sin ^4}\alpha - {\cos ^4}\alpha = - \sin 2\alpha \) |
Câu 4: Chọn đáp án đúng.
A. Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng |
C. Đồ thị hàm số chẵn nhận gốc tọa độ làm tâm đối xứng D. Cả A và C đều đúng |
Câu 5: Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu tương ứng là huyết áp tâm thu và tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số \(p\left( t \right) = 110 + 20\sin \left( {160\pi t} \right)\). Chọn đáp án đúng.
A. Chỉ số huyết áp của người này là 130/90 và chỉ số huyết áp là cao hơn mức bình thường. B. Chỉ số huyết áp của người này là 130/80 và chỉ số huyết áp là cao hơn mức bình thường. |
C. Chỉ số huyết áp của người này là 110/70 và chỉ số huyết áp là thấp hơn mức bình thường. D. Chỉ số huyết áp của người này là 110/75 và chỉ số huyết áp là thấp hơn mức bình thường. |
Câu 6: Sử dụng máy tính cầm tay để giải phương trình \(\sqrt 3 \tan x - 3 = 0\) với kết quả là radian (làm tròn kết quả đến hàng phần trăm) là:
A. \(x \approx - 1,05 + k\pi ,k \in \mathbb{Z}\) | B. \(x \approx 1,05 + k\pi ,k \in \mathbb{Z}\) |
C. Cả A và B đều đúng | D. Cả A và B đều sai |
Câu 7: Tìm tất cả các tham số thực m để phương trình \({\sin ^2}x + \sin x\cos x = m\) có nghiệm.
A. \(m \le \frac{{1 - \sqrt 2 }}{2};\frac{{1 + \sqrt 2 }}{2} \le m\) | B. \(\frac{{1 - \sqrt 2 }}{2} \le m \le \frac{{1 + \sqrt 2 }}{2}\) |
C. \(m \le \frac{{1 - \sqrt 2 }}{2}\) | D. \(m \le \frac{{1 + \sqrt 2 }}{2}\) |
Câu 8: Dãy số có các số hạng đầu là \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};...\) Số hạng tổng quát của dãy số này là:
A. \({u_n} = \frac{{n + 1}}{{n - 1}}\) | B. \({u_n} = \frac{{n + 1}}{n}\) |
C. \({u_n} = \frac{{n - 1}}{n}\) | D. \({u_n} = \frac{{{n^2} - n}}{{n - 1}}\) |
Câu 9: Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{n^2}}},\forall n = 2;{\rm{ }}3;{\rm{ }}4; \cdots .\) Mệnh đề nào sau đây đúng?
A. Dãy số \(\left( {{u_n}} \right)\) bị chặn trên và không bị chặn dưới B. Dãy số \(\left( {{u_n}} \right)\) bị chặn dưới và không bị chặn trên |
C. Dãy số \(\left( {{u_n}} \right)\) bị chặn D. Dãy số \(\left( {{u_n}} \right)\) không bị chặn |
Câu 10: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng?
A. \({u_n} = 8 - {3^n}\) | B. \({u_n} = \frac{8}{{{3^n}}}\) |
C. \({u_n} = {8.3^n}\) | D. \({u_n} = 8 - 3n\) |
Câu 11: Một công ty thực hiện việc trả lương cho các kỹ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là 14 triệu đồng/ quý và kể từ quý làm việc thứ hai, mức lương sẽ được tăng 500 000 đồng mỗi quý. Tổng số tiền một kỹ sư nhận được sau ba năm làm việc tại công ty là:
A. 205 triệu đồng | B. 201 triệu đồng |
C. 209 triệu đồng | D. 203 triệu đồng |
Câu 12: Cho ba góc của một tam giác lập thành một cấp số cộng, trong đó góc lớn nhất gấp đôi góc nhỏ nhất. Số đo góc lớn nhất của tam giác là:
A. \({70^0}\) | B. \({90^0}\) |
C. \({60^0}\) | D. \({80^0}\) |
Câu 13: Dãy số gồm các số tự nhiên lẻ nhỏ hơn 20, sắp xếp theo thứ tự từ bé đến lớn là:
A. Dãy số hữu hạn: \(1;3;5;7;9;11;13;15;17;19\) | B. Dãy số vô hạn: \(19;17;15;13;11;9;7;5;3;1\) |
C. Dãy số vô hạn: \(1;3;5;7;9;11;13;15;17;19\) | D. Dãy số hữu hạn: \(19;17;15;13;11;9;7;5;3;1\) |
Câu 14: Hình nào trong các hình sau đây là hình chóp tứ giác?
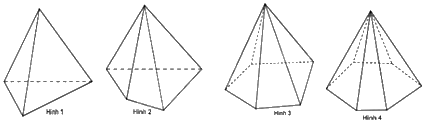
A. Hình 1 | B. Hình 2 |
C. Hình 3 | D. Hình 4 |
Câu 15: Cho tam giác ABC và điểm S không nằm trong mặt phẳng chứa tam giác ABC. Có bao nhiêu mặt phẳng được tạo thành?
A. 6 mặt phẳng | B. 2 mặt phẳng |
C. 3 mặt phẳng | D. 4 mặt phẳng |
Câu 16: Cho hình chóp S. ABCD có đáy ABCD là hình thang với AB là đáy lớn. Trên đoạn SA, lấy điểm I không trùng với S và A; trên đoạn BC lấy điểm J không trùng với B và C. Giao tuyến của đường thẳng IJ và mặt phẳng (SBD) là:
A. Điểm H là giao điểm SK và IJ, với K là giao điểm của AJ và BD | B. Điểm H là giao điểm SE và IJ, với E là giao điểm của AD và BC |
C. Điểm H là giao điểm SD và IJ | D. Điểm H là giao điểm BD và IJ |
Câu 17: Cho hình chóp tam giác S. ABC. Trong các cặp đường thẳng sau, cặp đường thẳng nào không chéo nhau?
A. SA và BC | B. AB và SC |
C. SB và SC | D. AC và SB |
Câu 18: Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và ABD. Gọi M, N lần lượt là trung điểm của BC và BD. Trong các đường thẳng MN, CD, BD, BC thì IJ song song với bao nhiêu đường thẳng?
A. 1 | B. 2 |
C. 3 | D. 4 |
Câu 19: Cho hình chóp tứ giác S. ABCD có M, N, I, K lần lượt là trung điểm của SA, SC, AD, CD. Tứ giác MNKI là hình gì?
A. Hình thoi | B. Hình vuông |
C. Hình chữ nhật | D. Hình bình hành |
Câu 20: Cho các số a, b, c \(\left( {a < b < c,c \in \mathbb{Z}} \right)\) lập thành cấp số nhân; đồng thời \(a,b + 8,c\) theo thứ tự lập thành cấp số cộng và \(a,b + 8,c + 64\) theo thứ tự lập thành cấp số nhân. Giá trị biểu thức \(P = a + b + c\) là:
A. 52 | B. 54 |
C. 60 | D. 70 |
Phần tự luận (5 điểm)
Bài 1. (1,5 điểm)
1) Giải các phương trình sau:
a) \({\sin ^2}x - {\cos ^2}x + \cos 3x = 0\)
b) \(\sin x + \sqrt 3 \cos x = 0\)
2) Tìm giá trị nhỏ nhất, lớn nhất của hàm số \(y = 2{\sin ^2}x + \sqrt 3 \sin 2x\)
3) Phương trình \({\tan ^4}x + 1 = \frac{{\left( {2 - {{\sin }^2}2x} \right)\sin 3x}}{{{{\cos }^4}x}}\) có bao nhiêu nghiệm thuộc \(\left( {\frac{\pi }{2};\pi } \right)\)?
Bài 2. (1,5 điểm)
a) Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 4,{u_2} = 10.\) Tính \({u_{100}}\).
b) Cho dãy số \(\left( {{u_n}} \right)\): \(\left( {{u_n}} \right):\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = \sqrt {1 + u_n^2} \end{array} \right.\). Tìm công thức số hạng tổng quát của dãy số trên.
Bài 3. (1,0 điểm) Cho hình chóp S. ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của SB. N là điểm trên cạnh BC sao cho \(BN = 2CN\). Xác định giao tuyến của mặt phẳng (SCD) và mặt phẳng (AMN).
Bài 4. (1,0 điểm)
a) Cho hình chóp S. ABCD có đáy là hình thang với đáy lớn là AB. Gọi I, J lần lượt là trung điểm của AD và BC và G là trọng tâm của tam giác SAB. Tìm giao tuyến của mặt phẳng (SAB) và mặt phẳng (IJG)
b) Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi \({G_1},{G_2}\) lần lượt là trọng tâm các tam giác SAB và SCD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng \({G_1}{G_2}\)//AD//BC
-------- Hết --------
Lời giải chi tiết
Phần trắc nghiệm (5 điểm)
Câu 1: C | Câu 2: D | Câu 3: B | Câu 4: A | Câu 5: A |
Câu 6: B | Câu 7: B | Câu 8: C | Câu 9: C | Câu 10: D |
Câu 11: B | Câu 12: D | Câu 13: A | Câu 14: B | Câu 15: D |
Câu 16: A | Câu 17: C | Câu 18: B | Câu 19: D | Câu 20: A |
Câu 1: Góc lượng giác nào dưới đây tương ứng với chuyển động quay \(3\frac{2}{5}\) vòng ngược chiều kim đồng hồ?
A. \(1\;{224^0}\) | B. \(\frac{{34\pi }}{5}rad\) |
C. Cả A và B đều đúng | D. Cả A và B đều sai. |
Phương pháp
Một vòng quay của kim đồng hồ ứng với 360 độ, \({1^\circ } = \frac{\pi }{{180}}{\rm{ rad}} \) và \( 1{\rm{rad}} = {\left( {\frac{{180}}{\pi }} \right)^\circ }{\rm{. }}\)
Quy ước chiều quay ngược với chiều kim đồng hồ là chiều dương.
Lời giải
\(3\frac{2}{5}\) vòng đường tròn ứng với: \(3\frac{2}{5}{.360^0} = 1\;{224^0} = \frac{{34\pi }}{5}rad\)
Đáp án C
Câu 2: Chọn đáp án đúng:
A. \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = \frac{1}{2}\tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\) B. \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = 2\tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\) |
C. \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = \tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\) D. \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = 3\tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\) |
Phương pháp
Sử dụng công thức: \(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha ,\tan \alpha .\cot \alpha = 1,{\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Lời giải
Ta có: \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = \sqrt {{{\sin }^4}x + 4\left( {1 - {{\sin }^2}x} \right)} + \sqrt {{{\cos }^4}x + 4\left( {1 - {{\cos }^2}x} \right)} \)
\( = \sqrt {{{\left( {{{\sin }^2}x} \right)}^2} - 4{{\sin }^2}x + 4} + \sqrt {{{\left( {{{\cos }^2}x} \right)}^2} - 4{{\cos }^2}x + 4} = \sqrt {{{\left( {{{\sin }^2}x - 2} \right)}^2}} + \sqrt {{{\left( {{{\cos }^2}x - 2} \right)}^2}} \)
\( = \left( {2 - {{\sin }^2}x} \right) + \left( {2 - {{\cos }^2}x} \right) = 4 - \left( {{{\sin }^2}x + {{\cos }^2}x} \right) = 3\)
Lại có: \(\left( {x + \frac{\pi }{3}} \right) + \left( {\frac{\pi }{6} - x} \right) = \frac{\pi }{2} \Rightarrow \tan \left( {\frac{\pi }{6} - x} \right) = \cot \left( {x + \frac{\pi }{3}} \right) \Rightarrow \tan \left( {\frac{\pi }{6} - x} \right).\tan \left( {x + \frac{\pi }{3}} \right) = 1\)
Do đó: \(\sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} = 3\tan \left( {x + \frac{\pi }{3}} \right)\tan \left( {\frac{\pi }{6} - x} \right)\)
Đáp án D
Câu 3: Chọn khẳng định đúng:
A. \({\sin ^4}\alpha - {\cos ^4}\alpha = \cos 2\alpha \) | B. \({\sin ^4}\alpha - {\cos ^4}\alpha = - \cos 2\alpha \) |
C. \({\sin ^4}\alpha - {\cos ^4}\alpha = \sin 2\alpha \) | D. \({\sin ^4}\alpha - {\cos ^4}\alpha = - \sin 2\alpha \) |
Phương pháp
Sử dụng công thức: \({\cos ^2}\alpha - {\sin ^2}\alpha = \cos 2\alpha ,{\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
Lời giải
\({\sin ^4}\alpha - {\cos ^4}\alpha = {\left( {{{\sin }^2}\alpha } \right)^2} - {\left( {{{\cos }^2}\alpha } \right)^2} \\= \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\left( {{{\sin }^2}\alpha - {{\cos }^2}\alpha } \right) = {\sin ^2}\alpha - {\cos ^2}\alpha \\= - \cos 2\alpha \)
Đáp án B
Câu 4: Chọn đáp án đúng.
A. Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng |
C. Đồ thị hàm số chẵn nhận gốc tọa độ làm tâm đối xứng D. Cả A và C đều đúng |
Phương pháp
+ Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
+ Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Lời giải
+ Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.
+ Đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Đáp án A
Câu 5: Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng các mô trong cơ thể. Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu tương ứng là huyết áp tâm thu và tâm trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số \(p\left( t \right) = 110 + 20\sin \left( {160\pi t} \right)\). Chọn đáp án đúng.
A. Chỉ số huyết áp của người này là 130/90 và chỉ số huyết áp là cao hơn mức bình thường. B. Chỉ số huyết áp của người này là 130/80 và chỉ số huyết áp là cao hơn mức bình thường. |
C. Chỉ số huyết áp của người này là 110/70 và chỉ số huyết áp là thấp hơn mức bình thường. D. Chỉ số huyết áp của người này là 110/75 và chỉ số huyết áp là thấp hơn mức bình thường. |
Phương pháp
Sử dụng kiến thức: \( - 1 \le \sin \alpha \le 1\)
Lời giải
Ta có: \( - 1 \le \sin \left( {160\pi t} \right) \le 1\forall t \in \mathbb{R} \Leftrightarrow - 20 \le 20\sin \left( {160\pi t} \right) \le 20\forall t \in \mathbb{R}\)
\( \Leftrightarrow 90 \le 110 + 20\sin \left( {160\pi t} \right) \le 130\;\forall t \in \mathbb{R}\)
Vậy chỉ số huyết áp của người này là 130/90 và chỉ số huyết áp của người này là cao hơn mức bình thường.
Đáp án A
Câu 6: Sử dụng máy tính cầm tay để giải phương trình \(\sqrt 3 \tan x - 3 = 0\) với kết quả là radian (làm tròn kết quả đến hàng phần trăm) là:
A. \(x \approx - 1,05 + k\pi ,k \in \mathbb{Z}\) | B. \(x \approx 1,05 + k\pi ,k \in \mathbb{Z}\) |
C. Cả A và B đều đúng | D. Cả A và B đều sai |
Phương pháp
Sử dụng máy tính cầm tay để tìm nghiệm của phương trình.
Lời giải
Ta có: \(\sqrt 3 \tan x - 3 = 0 \Leftrightarrow \tan x = \sqrt 3 \)
Sau khi chuyển máy tính sang chế độ “radian”. Bấm liên tiếp

Ta được kết quả gần đúng là 1,05.
Vậy phương trình \(\sqrt 3 \tan x - 3 = 0\) có các nghiệm là \(x \approx 1,05 + k\pi ,k \in \mathbb{Z}\).
Đáp án B
Câu 7: Tìm tất cả các tham số thực m để phương trình \({\sin ^2}x + \sin x\cos x = m\) có nghiệm.
A. \(m \le \frac{{1 - \sqrt 2 }}{2};\frac{{1 + \sqrt 2 }}{2} \le m\) | B. \(\frac{{1 - \sqrt 2 }}{2} \le m \le \frac{{1 + \sqrt 2 }}{2}\) |
C. \(m \le \frac{{1 - \sqrt 2 }}{2}\) | D. \(m \le \frac{{1 + \sqrt 2 }}{2}\) |
Phương pháp
Sử dụng kiến thức: Phương trình \(a\sin x + b\cos x = c\) có nghiệm khi \({c^2} \le {a^2} + {b^2}\)
Lời giải
\({\sin ^2}x + \sin x\cos x = m \Leftrightarrow \frac{{1 - \cos 2x}}{2} + \frac{1}{2}\sin 2x = m \Leftrightarrow 1 - \cos 2x + \sin 2x = 2m\)
\( \Leftrightarrow - \cos 2x + \sin 2x = 2m - 1\) (1)
Phương trình (1) có nghiệm khi và chỉ khi
\({\left( { - 1} \right)^2} + {1^2} \ge {\left( {2m - 1} \right)^2} \Leftrightarrow {\left( {2m - 1} \right)^2} \le 2 \Leftrightarrow - \sqrt 2 \le 2m - 1 \le \sqrt 2 \Leftrightarrow \frac{{1 - \sqrt 2 }}{2} \le m \le \frac{{1 + \sqrt 2 }}{2}\)
Đáp án B
Câu 8: Dãy số có các số hạng đầu là \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};...\) Số hạng tổng quát của dãy số này là:
A. \({u_n} = \frac{{n + 1}}{{n - 1}}\) | B. \({u_n} = \frac{{n + 1}}{n}\) |
C. \({u_n} = \frac{{n - 1}}{n}\) | D. \({u_n} = \frac{{{n^2} - n}}{{n - 1}}\) |
Phương pháp
Tìm công thức số hạng tổng quát của dãy số \(\left( {{u_n}} \right)\): Từ các số đã cho của dãy số, biến đổi sao cho các số hạng có chung một quy luật theo n, từ đó tìm được công thức số hạng tổng quát \({u_n}\).
Lời giải
Ta có: \({u_1} = 0 = \frac{{1 - 1}}{1};{u_2} = \frac{1}{2} = \frac{{2 - 1}}{2};{u_3} = \frac{2}{3} = \frac{{3 - 1}}{3};{u_4} = \frac{3}{4} = \frac{{4 - 1}}{4};{u_5} = \frac{4}{5} = \frac{{5 - 1}}{5};...\)
Dự đoán công thức số hạng tổng quát: \({u_n} = \frac{{n - 1}}{n}\).
Đáp án C
Câu 9: Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + ... + \frac{1}{{{n^2}}},\forall n = 2;{\rm{ }}3;{\rm{ }}4; \cdots .\) Mệnh đề nào sau đây đúng?
A. Dãy số \(\left( {{u_n}} \right)\) bị chặn trên và không bị chặn dưới B. Dãy số \(\left( {{u_n}} \right)\) bị chặn dưới và không bị chặn trên |
C. Dãy số \(\left( {{u_n}} \right)\) bị chặn D. Dãy số \(\left( {{u_n}} \right)\) không bị chặn |
Phương pháp
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số bị chặn trên nếu tồn tại một số M sao cho \({u_n} \le M\;\forall n \in \mathbb{N}*\).
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số bị chặn dưới nếu tồn tại một số m sao cho \({u_n} \ge m\;\forall n \in \mathbb{N}*\).
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, nghĩa là tồn tại các số M và m sao cho \(m \le {u_n} \le M\;\forall n \in \mathbb{N}*\).
Lời giải
Ta có \({u_n} > 0\;\forall n = 2;{\rm{ }}3;{\rm{ }}4; \cdots \) nên \({u_n}\) bị chặn dưới bởi 0.
Mặt khác \(\frac{1}{{{k^2}}} < \frac{1}{{\left( {k - 1} \right)k}}\,\, = \frac{1}{{k - 1}} - \frac{1}{k}\,\,\left( {k \in {\mathbb{N}^*},\,k \ge 2} \right)\) nên suy ra:
\({u_n} < \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + \cdots + \frac{1}{{n\left( {n + 1} \right)}} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{2} - \frac{1}{4} + \cdots + \frac{1}{n} - \frac{1}{{n + 1}} = 1 - \frac{1}{{n + 1}} < 1\)
Do đó, dãy \(\left( {{u_n}} \right)\) bị chặn trên. Vậy dãy số \(\left( {{u_n}} \right)\) bị chặn.
Đáp án C
Câu 10: Trong các dãy số được cho dưới đây, dãy số nào là cấp số cộng?
A. \({u_n} = 8 - {3^n}\) | B. \({u_n} = \frac{8}{{{3^n}}}\) |
C. \({u_n} = {8.3^n}\) | D. \({u_n} = 8 - 3n\) |
Phương pháp
Cấp số cộng là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó với một số không đổi d, tức là: \({u_n} = {u_{n - 1}} + d\) với \(n \ge 2\).
Lời giải
Xét dãy số: \({u_n} = 8 - 3n\), ta có: \({u_1} = 5;{u_2} = 2;{u_3} = - 1;{u_4} = - 4;..\)
Nhận thấy các số hạng, kể từ số hạng thứ hai trở đi, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với \( - 3\) nên dãy số \({u_n} = 8 - 3n\) là cấp số cộng
Đáp án D
Câu 11: Một công ty thực hiện việc trả lương cho các kỹ sư theo phương thức sau: Mức lương của quý làm việc đầu tiên cho công ty là 14 triệu đồng/ quý và kể từ quý làm việc thứ hai, mức lương sẽ được tăng 500 000 đồng mỗi quý. Tổng số tiền một kỹ sư nhận được sau ba năm làm việc tại công ty là:
A. 205 triệu đồng | B. 201 triệu đồng |
C. 209 triệu đồng | D. 203 triệu đồng |
Phương pháp
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d. Đặt \({S_n} = {u_1} + {u_2} + {u_3} + ... + {u_n}\).
Khi đó: \({S_n} = \frac{{\left( {{u_1} + {u_n}} \right)n}}{2} = \frac{{\left[ {2{u_1} + \left( {n - 1} \right)d} \right]n}}{2}\)
Lời giải
Gọi \({u_n}\) là mức lương của quý thứ n làm việc tại công ty.
Khi đó, dãy số \(\left( {{u_n}} \right)\) lập thành một cấp số cộng có số hạng đầu \({u_1} = 14\) và công sai \(d = 0,5\)
Một năm có 4 quý nên 3 năm có 12 quý. Do đó, để tính số tiền kỹ sư nhận được sau ba năm, ta đi tính tổng 12 số hạng đầu tiên của cấp số cộng.
Số tiền người kĩ sư nhận được là: \({S_{12}} = \frac{{12\left[ {2.14 + \left( {12 - 1} \right).0,5} \right]}}{2} = 201\) (triệu đồng)
Đáp án B
Câu 12: Cho ba góc của một tam giác lập thành một cấp số cộng, trong đó góc lớn nhất gấp đôi góc nhỏ nhất. Số đo góc lớn nhất của tam giác là:
A. \({70^0}\) | B. \({90^0}\) |
C. \({60^0}\) | D. \({80^0}\) |
Phương pháp
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát được xác định theo công thức \({u_n} = {u_1} + \left( {n - 1} \right)d\)
Lời giải
Không làm mất tính tổng quát, gọi ba góc A, B, C của tam giác ABC theo thứ tự từ bé đến lớn lập thành một cấp số cộng có công sai là d. Khi đó, \(\widehat B = \widehat A + d,\widehat C = \widehat B + d = \widehat A + 2d \Rightarrow \widehat A + \widehat C = 2\widehat B\)
Theo giả thiết ta có: \(\widehat A + \widehat B + \widehat C = {180^0},\widehat C = 2\widehat A\)
Do đó, ta có hệ phương trình: \(\left\{ \begin{array}{l}\widehat A + \widehat C = 2\widehat B\\\widehat A + \widehat B + \widehat C = {180^0}\\\widehat C = 2\widehat A\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\widehat A = {40^0}\\\widehat B = {60^0}\\\widehat C = {80^0}\end{array} \right.\)
Vậy góc có số đo lớn nhất là \({80^0}\)
Đáp án D
Câu 13: Dãy số gồm các số tự nhiên lẻ nhỏ hơn 20, sắp xếp theo thứ tự từ bé đến lớn là:
A. Dãy số hữu hạn: \(1;3;5;7;9;11;13;15;17;19\) | B. Dãy số vô hạn: \(19;17;15;13;11;9;7;5;3;1\) |
C. Dãy số vô hạn: \(1;3;5;7;9;11;13;15;17;19\) | D. Dãy số hữu hạn: \(19;17;15;13;11;9;7;5;3;1\) |
Phương pháp
Hàm số u xác định trên tập hợp \(M = \left\{ {1;2;3;..;m} \right\}\) thì được gọi là một dãy số hữu hạn. Dạng triển khai của dãy số này là \({u_1},{u_2},...,{u_m}\).
Lời giải
Dãy số gồm các số tự nhiên lẻ nhỏ hơn 20, sắp xếp theo thứ tự từ bé đến lớn là dãy số hữu hạn: \(1;3;5;7;9;11;13;15;17;19\)
Đáp án A
Câu 14: Hình nào trong các hình sau đây là hình chóp tứ giác?
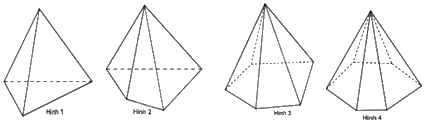
A. Hình 1 | B. Hình 2 |
C. Hình 3 | D. Hình 4 |
Phương pháp
Cho đa giác lồi \({A_1}{A_2}{A_3}....{A_n}\) nằm trong mặt phẳng \(\left( \alpha \right)\) và điểm S không thuộc \(\left( \alpha \right)\). Nối S với các đỉnh \({A_1};{A_2};{A_3};...;{A_n}\) ta được n tam giác \(S{A_1}{A_2};S{A_2}{A_3};...;S{A_n}{A_1}\). Hình được tạo bởi n tam giác đó và đa giác \({A_1}{A_2}{A_3}....{A_n}\) được gọi là hình chóp, kí hiệu là \(S.{A_1}{A_2}{A_3}....{A_n}\).
Lời giải
Hình 2 là hình chóp tứ giác.
Đáp án B
Câu 15: Cho tam giác ABC và điểm S không nằm trong mặt phẳng chứa tam giác ABC. Có bao nhiêu mặt phẳng được tạo thành?
A. 6 mặt phẳng | B. 2 mặt phẳng |
C. 3 mặt phẳng | D. 4 mặt phẳng |
Phương pháp
Một mặt phẳng được xác định nếu biết nó chứa ba điểm không thẳng hàng.
Lời giải
Các mặt phẳng được tạo thành là: (SAB), (SAC), (SBC), (ABC). Vậy có 4 mặt phẳng được tạo thành.
Đáp án D
Câu 16: Cho hình chóp S. ABCD có đáy ABCD là hình thang với AB là đáy lớn. Trên đoạn SA, lấy điểm I không trùng với S và A; trên đoạn BC lấy điểm J không trùng với B và C. Giao tuyến của đường thẳng IJ và mặt phẳng (SBD) là:
A. Điểm H là giao điểm SK và IJ, với K là giao điểm của AJ và BD | B. Điểm H là giao điểm SE và IJ, với E là giao điểm của AD và BC |
C. Điểm H là giao điểm SD và IJ | D. Điểm H là giao điểm BD và IJ |
Phương pháp
Cách tìm giao điểm của đường thẳng d và mặt phẳng \(\left( \alpha \right)\):
Trường hợp 1: \(\left( \alpha \right)\) chứa đường thẳng d’ và d’ cắt đường thẳng d tại I.
Khi đó, \(I = d \cap d' \Rightarrow I = d \cap \left( \alpha \right)\)
Trường hợp 2: \(\left( \alpha \right)\) không chứa đường thẳng nào cắt d.
+ Tìm mặt phẳng \(\left( \beta \right)\) chứa d và \(\left( \alpha \right) \cap \left( \beta \right) = d'\)
+ Tìm \(I = d \cap d'\). Khi đó, \(I = d \cap \left( \alpha \right)\)
Lời giải
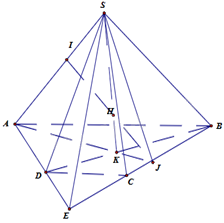
Trong mặt phẳng (ABCD), gọi K là giao điểm của AJ và BD nên K thuộc mặt phẳng (SBD) và mặt phẳng (SAJ).
Lại có, S thuộc mặt phẳng (SBD) và mặt phẳng (SAJ).
Do đó, \(SK = mp\left( {SAJ} \right) \cap mp\left( {SBD} \right)\)
Trong mặt phẳng (SAJ), gọi H là giao điểm của SK và IJ.
Vì \(H \in IJ,H \in SK \subset mp\left( {SBD} \right)\)
Vậy H là giao điểm của SK và mặt phẳng (SBD).
Đáp án A
Câu 17: Cho hình chóp tam giác S. ABC. Trong các cặp đường thẳng sau, cặp đường thẳng nào không chéo nhau?
A. SA và BC | B. AB và SC |
C. SB và SC | D. AC và SB |
Phương pháp
Nếu không có mặt phẳng nào chứa hai đường thẳng a và b thì khi đó ta nói đường thẳng a và b chéo nhau.
Lời giải
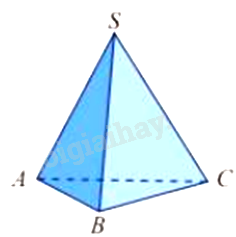
Hai đường thẳng SB và SC cùng nằm trong mặt phẳng (SBC) nên hai đường thẳng này không chéo nhau.
Đáp án C
Câu 18: Cho tứ diện ABCD. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và ABD. Gọi M, N lần lượt là trung điểm của BC và BD. Trong các đường thẳng MN, CD, BD, BC thì IJ song song với bao nhiêu đường thẳng?
A. 1 | B. 2 |
C. 3 | D. 4 |
Phương pháp
Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Lời giải
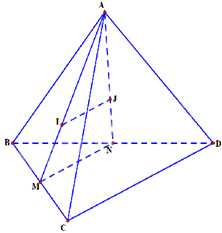
Vì M, N lần lượt là trung điểm của BC và BD nên MN là đường trung bình của tam giác BCD. Do đó, MN//CD
Vì I là trọng tâm tam giác ABC nên \(\frac{{AI}}{{AM}} = \frac{2}{3}\)
Vì J là trọng tâm tam giác ABD nên \(\frac{{AJ}}{{AN}} = \frac{2}{3}\)
Do đó, \(\frac{{AJ}}{{AN}} = \frac{{AI}}{{AM}}\) nên IJ//MN (định lí Thalès đảo)
Vì IJ//MN, MN//CD nên IJ//CD
Vậy đường thẳng IJ song song với hai đường thẳng là MN và CD.
Đáp án B
Câu 19: Cho hình chóp tứ giác S. ABCD có M, N, I, K lần lượt là trung điểm của SA, SC, AD, CD. Tứ giác MNKI là hình gì?
A. Hình thoi | B. Hình vuông |
C. Hình chữ nhật | D. Hình bình hành |
Phương pháp
Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Lời giải
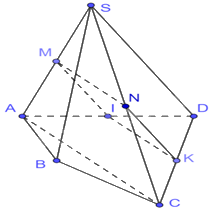
Vì M, N lần lượt là trung điểm của SA, SC nên MN là đường trung bình của tam giác SAC. Do đó, MN//AC, \(MN = \frac{1}{2}AC\)
Vì I, K lần lượt là trung điểm của DA, DC nên IK là đường trung bình của tam giác DAC. Do đó, IK//AC, \(IK = \frac{1}{2}AC\)
Do đó, IK//MN, \(IK = MN\). Vậy tứ giác MNKI là hình bình hành.
Đáp án D
Câu 20: Cho các số a, b, c \(\left( {a < b < c,c \in \mathbb{Z}} \right)\) lập thành cấp số nhân; đồng thời \(a,b + 8,c\) theo thứ tự lập thành cấp số cộng và \(a,b + 8,c + 64\) theo thứ tự lập thành cấp số nhân. Giá trị biểu thức \(P = a + b + c\) là:
A. 52 | B. 54 |
C. 60 | D. 70 |
Phương pháp
Cấp số nhân \(\left( {{u_n}} \right)\) có số hạng đầu là \({u_1}\) và công bội q thì số hạng tổng quát \({u_n}\) của nó được xác định bởi công thức \({u_n} = {u_1}.{q^{n - 1}}\) với \(n \ge 2\).
Lời giải
Theo đầu bài ta có hệ phương trình: \(\left\{ \begin{array}{l}ac = {b^2}\\a + c = 2\left( {b + 8} \right)\\a\left( {c + 64} \right) = {\left( {b + 8} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}ac = {b^2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\a - 2b = 16 - c\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\\ac + 64a = {\left( {b + 8} \right)^2}\,\,\,\,\,\left( 3 \right)\end{array} \right..\)
Thay (1) vào (3) ta có: \({b^2} + 64a = {b^2} + 16b + 64 \Leftrightarrow 4a - b = 4\,\,\left( 4 \right).\)
Kết hợp (2) và (4) ta có: \(\left\{ \begin{array}{l}a - 2b = 16 - c\\4a - b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{c - 8}}{7}\\b = \frac{{4c - 60}}{7}\end{array} \right.\,\,\,\,\,\left( 5 \right)\)\(\)
Thay (5) vào (1) ta có: \(7\left( {c - 8} \right)c = {\left( {4c - 60} \right)^2} \Leftrightarrow 9{c^2} - 424c + 3600 = 0 \Leftrightarrow \left[ \begin{array}{l}c = 36\\c = \frac{{100}}{9}\end{array} \right. \Leftrightarrow c = 36\,\,\left( {c \in \mathbb{Z}} \right).\)
Với \(c = 36 \Rightarrow a = 4,b = 12 \Rightarrow P = 36 + 4 + 12 = 52\)
Đáp án A
Phần tự luận (5 điểm)
Bài 1. (1,5 điểm)
1) Giải các phương trình sau:
a) \({\sin ^2}x - {\cos ^2}x + \cos 3x = 0\)
b) \(\sin x + \sqrt 3 \cos x = 0\)
2) Tìm giá trị nhỏ nhất, lớn nhất của hàm số \(y = 2{\sin ^2}x + \sqrt 3 \sin 2x\)
3) Phương trình \({\tan ^4}x + 1 = \frac{{\left( {2 - {{\sin }^2}2x} \right)\sin 3x}}{{{{\cos }^4}x}}\) có bao nhiêu nghiệm thuộc \(\left( {\frac{\pi }{2};\pi } \right)\)?
Phương pháp
1) a) + Xét phương trình \(\cos x = m\)
* Nếu \(\left| m \right| > 1\) thì phương trình vô nghiệm.
* Nếu \(\left| m \right| \le 1\) thì phương trình có nghiệm: \(x = \alpha + k2\pi ,k \in \mathbb{Z}\) và \(x = - \alpha + k2\pi ,k \in \mathbb{Z}\), với \(\alpha \) là góc thuộc \(\left[ {0;\pi } \right]\) sao cho \(\cos \alpha = m\)
b) \(\sin \alpha = 0 \Leftrightarrow \alpha = k\pi \left( {k \in \mathbb{Z}} \right)\)
2) Sử dụng kiến thức \( - 1 \le \sin x \le 1\)
3) + tanx xác định khi \(\cos x \ne 0\)
+ Xét phương trình \(\sin x = m\)
* Nếu \(\left| m \right| > 1\) thì phương trình vô nghiệm.
* Nếu \(\left| m \right| \le 1\) thì phương trình có nghiệm: \(x = \alpha + k2\pi ,k \in \mathbb{Z}\) và \(x = \pi - \alpha + k2\pi ,k \in \mathbb{Z}\), với \(\alpha \) là góc thuộc \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) sao cho \(\sin \alpha = m\)
Lời giải
1)
a) \({\sin ^2}x - {\cos ^2}x + \cos 3x = 0 \Leftrightarrow \cos 3x - \cos 2x = 0 \Leftrightarrow \cos 3x = \cos 2x\)
\( \Leftrightarrow \left[ \begin{array}{l}3x = 2x + k2\pi \\3x = - 2x + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = k2\pi \\x = \frac{{k2\pi }}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình đã cho có họ nghiệm là \(x = k2\pi ,x = \frac{{k2\pi }}{5}\left( {k \in \mathbb{Z}} \right)\)
b) \(\sin x + \sqrt 3 \cos x = 0 \Leftrightarrow \frac{1}{2}\sin x + \frac{{\sqrt 3 }}{2}\cos x = 0 \Leftrightarrow \cos \frac{\pi }{3}\sin x + \sin \frac{\pi }{3}\cos x = 0\)
\( \Leftrightarrow \sin \left( {x + \frac{\pi }{3}} \right) = 0 \Leftrightarrow x + \frac{\pi }{3} = k\pi \left( {k \in \mathbb{Z}} \right) \Leftrightarrow x = - \frac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình đã cho có họ nghiệm là \(x = - \frac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)\)
2) Ta có: \(y = 2{\sin ^2}x + \sqrt 3 \sin 2x = 1 - \cos 2x + \sqrt 3 \sin 2x\)
\( = \sqrt 3 \sin 2x - \cos 2x + 1 = 2\left( {\frac{{\sqrt 3 }}{2}\sin 2x - \frac{1}{2}\cos 2x} \right) + 1\)
\( = 2\left( {\sin 2x\cos \frac{\pi }{6} - \sin \frac{\pi }{6}\cos 2x} \right) + 1 = 2\sin \left( {2x - \frac{\pi }{6}} \right) + 1.\)
Mà \( - 1 \le \sin \left( {2x - \frac{\pi }{6}} \right) \le 1 \Rightarrow - 1 \le 1 + 2\sin \left( {2x - \frac{\pi }{6}} \right) \le 3 \Rightarrow - 1 \le y \le 3.\)
Do đó, giá trị nhỏ nhất của hàm số là \( - 1\), giá trị lớn nhất của hàm số là 3.
3) Điều kiện: \(\cos x \ne 0\)
\({\tan ^4}x + 1 = \frac{{\left( {2 - {{\sin }^2}2x} \right)\sin 3x}}{{{{\cos }^4}x}} \Leftrightarrow {\sin ^4}x + {\cos ^4}x = \left( {2 - {{\sin }^2}2x} \right)\sin 3x\)
\( \Leftrightarrow {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x{\cos ^2}x = \left( {2 - {{\sin }^2}2x} \right)\sin 3x\)
\( \Leftrightarrow 1 - \frac{1}{2}{\sin ^2}2x = \left( {2 - {{\sin }^2}2x} \right)\sin 3x \Leftrightarrow 2 - {\sin ^2}2x = 2\left( {2 - {{\sin }^2}2x} \right)\sin 3x\)
\( \Leftrightarrow \left( {2 - {{\sin }^2}2x} \right)\left( {1 - 2\sin 3x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}2 - {\sin ^2}2x = 0\\1 - 2\sin 3x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sin 2x = \pm \sqrt 2 \left( {VL} \right)\\\sin 3x = \frac{1}{2}\end{array} \right.\)
\( \Leftrightarrow \sin 3x = \sin \frac{\pi }{6} \Leftrightarrow \left[ \begin{array}{l}3x = \frac{\pi }{6} + k2\pi \\3x = \pi - \frac{\pi }{6} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{18}} + \frac{{k2\pi }}{3}\\x = \frac{{5\pi }}{{18}} + \frac{{k2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\) (thỏa mãn điều kiện)
Lại có: \(x \in \left( {\frac{\pi }{2};\pi } \right)\) nên \(\left[ \begin{array}{l}\frac{\pi }{2} < \frac{\pi }{{18}} + \frac{{k2\pi }}{3} < \pi \\\frac{\pi }{2} < \frac{{5\pi }}{{18}} + \frac{{k2\pi }}{3} < \pi \end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}\frac{2}{3} < k < \frac{{17}}{{12}}\\\frac{1}{3} < k < \frac{{13}}{{12}}\end{array} \right.\left( {k \in \mathbb{Z}} \right) \Leftrightarrow \left[ \begin{array}{l}k = 1\\k = 1\end{array} \right.\)
Với \(k = 1\) thì \(x = \frac{{13\pi }}{{18}}\) hoặc \(x = \frac{{17\pi }}{{18}}\) (thỏa mãn điều kiện). Vậy có hai nghiệm thuộc \(\left( {\frac{\pi }{2};\pi } \right)\)
Bài 2. (1,5 điểm)
a) Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 4,{u_2} = 10.\) Tính \({u_{100}}\).
b) Cho dãy số \(\left( {{u_n}} \right)\): \(\left( {{u_n}} \right):\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = \sqrt {1 + u_n^2} \end{array} \right.\). Tìm công thức số hạng tổng quát của dãy số trên.
Phương pháp
a) Nếu một cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\) của nó được xác định bởi công thức: \({u_n} = {u_1} + \left( {n - 1} \right)d,n \ge 2\)
b) Công thức truy hồi là hệ thức biểu thị số hạng thứ n của dãy số qua số hạng (hay vài số hạng) đứng trước nó.
Lời giải
a) Ta có: \(d = {u_2} - {u_1} = 10 - 4 = 6\). Do đó, \({u_{100}} = {u_1} + \left( {100 - 1} \right)d = 4 + 99.6 = 598\)
b) Ta có
\(\begin{array}{l}{u_1} = 3 = \sqrt {{3^2} + 0} \\{u_2} = \sqrt {10} = \sqrt {{3^2} + 1} \\{u_3} = \sqrt {11} = \sqrt {{3^2} + 2} \\{u_4} = \sqrt {12} = \sqrt {{3^2} + 3} \\...\\{u_n} = \sqrt {{3^2} + n - 1} \,\,\left( * \right)\end{array}\)
Vậy công thức số hạng tổng quát của dãy số là: \({u_n} = \sqrt {{3^2} + n - 1} \)
Bài 3. (1,0 điểm) Cho hình chóp S. ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của SB. N là điểm trên cạnh BC sao cho \(BN = 2CN\). Xác định giao tuyến của mặt phẳng (SCD) và mặt phẳng (AMN).
Phương pháp
Nếu hai mặt phân biệt (P) và (Q) có điểm chung thì chúng có một đường thẳng chung duy nhất d chứa tất cả các điểm chung của hai mặt phẳng đó. Đường thẳng d đó gọi là giao tuyến của hai mặt phẳng (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\)
Lời giải
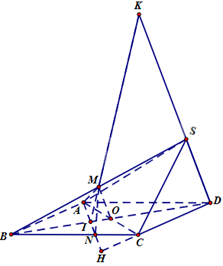
Trong mặt phẳng (ABCD), gọi H là giao điểm của AN và CD
Vì H thuộc AN nên H thuộc mặt phẳng (AMN), H thuộc DC nên H thuộc mặt phẳng (SCD).
Trong mặt phẳng (ABCD), gọi I là giao điểm của AN và BD nên I thuộc mặt phẳng (SBD).
Trong mặt phẳng (SBD), gọi K là giao điểm của IM và SD nên K thuộc mặt phẳng (AMN) và mặt phẳng (SCD).
Do đó, HK là giao tuyến của hai mặt phẳng (AMN) và mặt phẳng (SCD).
Bài 4. (1,0 điểm)
a) Cho hình chóp S. ABCD có đáy là hình thang với đáy lớn là AB. Gọi I, J lần lượt là trung điểm của AD và BC và G là trọng tâm của tam giác SAB. Tìm giao tuyến của mặt phẳng (SAB) và mặt phẳng (IJG)
b) Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi \({G_1},{G_2}\) lần lượt là trọng tâm các tam giác SAB và SCD. Gọi M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng \({G_1}{G_2}\)//AD//BC
Phương pháp
Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì song song với nhau.
Lời giải
a) VìI, J lần lượt là trung điểm của AD và BC nên IJ là đường trung bình của hình thang ABCD. Do đó, IJ//AB//CD. Ta có: G là điểm chung giữa hai mặt phẳng (SAB) và (IJG) Mà \(\left\{ \begin{array}{l}\left( {SAB} \right) \supset AB;\left( {IJG} \right) \supset IJ\\AB\parallel IJ\end{array} \right.\) Nên giao tuyến của mặt phẳng (SAB) và mặt phẳng (IJG) là đường thẳng qua G và song song với AB và IJ (đường thẳng PQ như hình vẽ). | 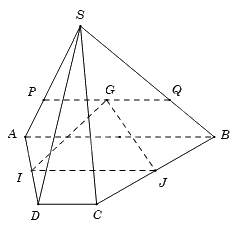 |
b) Vì \({G_1},{G_2}\) lần lượt là trọng tâm các tam giác SAB và SCD nên \(\frac{{S{G_1}}}{{SM}} = \frac{{S{G_2}}}{{SN}} = \frac{2}{3}\) nên MN//\({G_1}{G_2}\) Vì M, N lần lượt là trung điểm của AB, CD nên MN//AD//BC. Do đó, \({G_1}{G_2}\)//AD//BC | 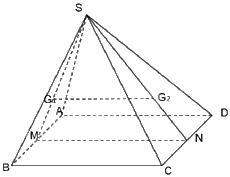 |
Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 4: Tổng quan và Hướng dẫn Ôn tập
Chào mừng các em học sinh lớp 11 đến với bài viết tổng quan về Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 4 do tusach.vn cung cấp. Đề thi này đóng vai trò quan trọng trong việc đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của các em sau một nửa học kỳ đầu tiên.
Cấu trúc Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 4
Đề thi được cấu trúc theo dạng đề thi giữa kỳ phổ biến hiện nay, bao gồm:
- Phần trắc nghiệm: Khoảng 5-7 câu, tập trung vào các kiến thức cơ bản, định nghĩa, tính chất và công thức.
- Phần tự luận: Khoảng 3-5 câu, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể.
Các chủ đề chính thường xuất hiện trong đề thi bao gồm:
- Hàm số lượng giác
- Phương trình lượng giác
- Đại lượng lượng giác của một góc bất kỳ
- Vecto trong mặt phẳng
- Tích vô hướng của hai vecto
- Ứng dụng của tích vô hướng
Tại sao nên luyện tập với Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 4?
Việc luyện tập với đề thi này mang lại nhiều lợi ích thiết thực cho các em:
- Làm quen với cấu trúc đề thi: Giúp các em hiểu rõ dạng đề thi, phân bổ thời gian hợp lý và tự tin hơn khi làm bài thi chính thức.
- Kiểm tra kiến thức: Đề thi giúp các em tự đánh giá mức độ nắm vững kiến thức và kỹ năng giải toán của mình.
- Rèn luyện kỹ năng: Việc giải đề thi giúp các em rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế.
- Tìm ra điểm yếu: Sau khi làm đề thi, các em có thể đối chiếu với đáp án để tìm ra những điểm yếu và tập trung ôn tập.
Hướng dẫn ôn tập hiệu quả cho Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo
Để đạt kết quả tốt nhất trong kỳ thi giữa kỳ, các em nên:
- Nắm vững kiến thức cơ bản: Đọc kỹ sách giáo khoa, ghi chép đầy đủ các kiến thức quan trọng và làm bài tập trong sách.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau, từ dễ đến khó, để rèn luyện kỹ năng giải toán.
- Học nhóm: Trao đổi kiến thức và kinh nghiệm với bạn bè để hiểu sâu hơn về các khái niệm và phương pháp giải toán.
- Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo hoặc các bạn học giỏi.
- Sử dụng tài liệu ôn tập: Tham khảo các tài liệu ôn tập, đề thi thử và đáp án chi tiết để chuẩn bị tốt nhất cho kỳ thi.
Tải Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 4 và Đáp án
Các em có thể tải Đề thi giữa kì 1 Toán 11 Chân trời sáng tạo - Đề số 4 và Đáp án chi tiết ngay tại tusach.vn. Chúng tôi luôn cập nhật những tài liệu ôn tập mới nhất và chất lượng nhất để giúp các em học tập tốt hơn.
Bảng so sánh các dạng bài tập thường gặp
| Dạng bài tập | Mức độ khó | Kỹ năng cần thiết |
|---|---|---|
| Giải phương trình lượng giác cơ bản | Dễ | Biến đổi lượng giác, sử dụng công thức |
| Giải phương trình lượng giác nâng cao | Trung bình | Sử dụng phương pháp đổi biến, phương pháp lượng giác hóa |
| Tính góc giữa hai vecto | Dễ | Sử dụng công thức tích vô hướng |
| Ứng dụng tích vô hướng để chứng minh đẳng thức hình học | Trung bình - Khó | Sử dụng kiến thức về hình học, tích vô hướng |
Chúc các em học tập tốt và đạt kết quả cao trong kỳ thi giữa kỳ!