Giải mục 3 trang 8 SGK Toán 10 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải Mục 3 Trang 8 SGK Toán 10 Tập 2 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 10 Tập 2 - Kết Nối Tri Thức. Bài viết này sẽ giúp bạn hiểu rõ cách giải Mục 3 trang 8, đồng thời cung cấp các kiến thức nền tảng cần thiết.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp bạn tự tin chinh phục môn Toán.
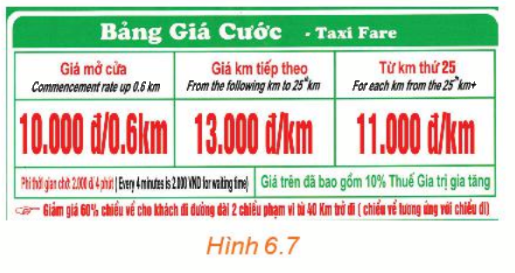
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7. a) Tính số tiền phải trả khi di chuyển 25 km. b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển. c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.
Luyện tập 3
Vẽ đồ thị của hàm số \(y = 3x + 1\) và \(y = - 2{x^2}\). Hãy cho biết:
a) Hàm số \(y = 3x + 1\)đồng biến hay nghịch biến trên \(\mathbb{R}\)
b) Hàm số \(y = - 2{x^2}\)đồng biến hay nghịch biến trên \(( - \infty ;0)\) và \((0; + \infty )\).
Phương pháp giải:
Quan sát đồ thị hàm số trên (a;b)
Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.
Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải.
Lời giải chi tiết:
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)
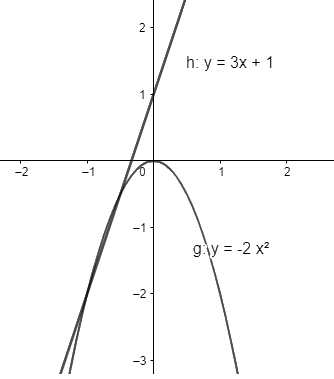
a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
HĐ6
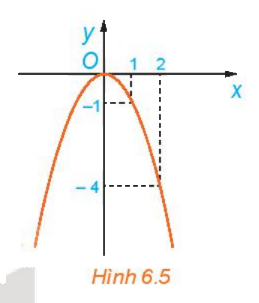
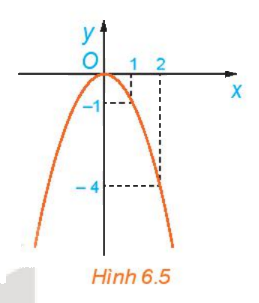
Quan sát đồ thị của hàm số \(y = f(x) = - {x^2}\) trên \(\mathbb{R}\)(H.6.5).
a) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng \(( - \infty ;0)\)?
b) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng \((0; + \infty )\)?
Lời giải chi tiết:
Dựa vào đồ thị, ta thấy:
a) Trên khoảng \(\left( { - \infty ;0} \right)\) , giá trị của f(x) tăng
b) Trên khoảng \(\left( {0; + \infty } \right)\) , giá trị của f(x) giảm
HĐ5
Cho hàm số \(y = - x + 1\) và \(y = x\). Tính giá trị y theo giá trị x để hoàn thành bảng sau:
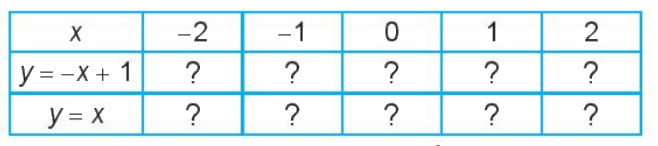
Khi giá trị x tăng, giá trị y tương ứng của mỗi hàm số \(y = - x + 1\) và \(y = x\) tăng hay giảm?
Lời giải chi tiết:
Thay x vào ta có:

Dựa vào bảng trên ta thấy:
Khi x tăng, giá trị y của hàm số y=-x+1 giảm
Khi x tăng, giá trị y của hàm số y=x tăng
Vận dụng 2
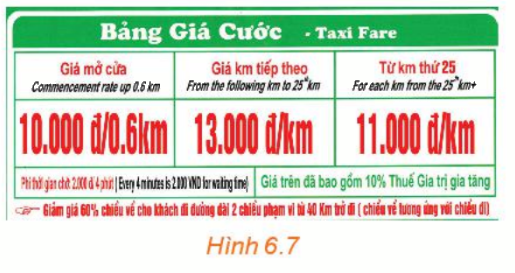
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.
a) Tính số tiền phải trả khi di chuyển 25 km.
b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.
c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.
Lời giải chi tiết:
Gọi x là số km taxi đã đi; y (nghìn đồng) là số tiền cước phải trả
a) Khi di chuyển 25km thì
Với 0,6km đầu tiên, số tiền cước phải trả 10000 (đồng)
Với những km tiếp theo, số tiền cước phải trả 13000.(25-0,6)=317200(đồng)
Vậy số tiền cước phải trả 317200+10000=327200(đồng)
b) Khi hành khách đi từ 0km đến 0,6km thì \(y = 10\)(nghìn đồng)
Khi hành khách đi từ 0,7km đến 25km thì \(y = 10 + (x - 0,6).13 = 13x + 2,2\)(nghìn đồng)
Khi khách hàng đi từ 25km trở lên \(y = 13.25 + 2,2 + (x - 25).11 = 11x + 52,2\) (nghìn đồng)
c) Vẽ đồ thị hàm số
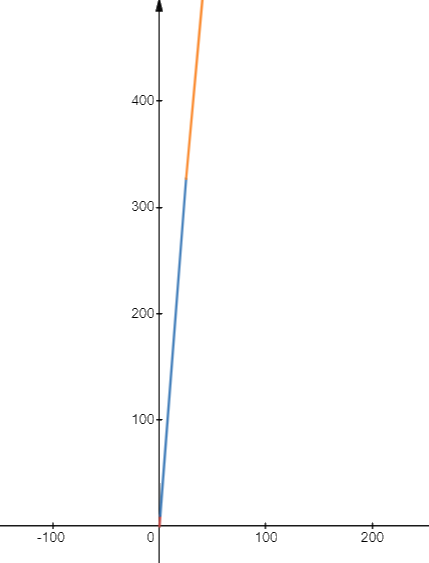
Nhìn trên đồ thị ta có thể thấy đồ thị đồng biến trên \(\left( {0; + \infty } \right)\)
- HĐ5
- HĐ6
- Luyện tập 3
- Vận dụng 2
Cho hàm số \(y = - x + 1\) và \(y = x\). Tính giá trị y theo giá trị x để hoàn thành bảng sau:
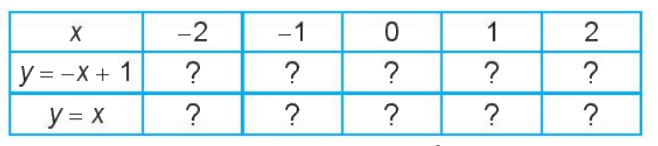
Khi giá trị x tăng, giá trị y tương ứng của mỗi hàm số \(y = - x + 1\) và \(y = x\) tăng hay giảm?
Lời giải chi tiết:
Thay x vào ta có:

Dựa vào bảng trên ta thấy:
Khi x tăng, giá trị y của hàm số y=-x+1 giảm
Khi x tăng, giá trị y của hàm số y=x tăng
Quan sát đồ thị của hàm số \(y = f(x) = - {x^2}\) trên \(\mathbb{R}\)(H.6.5).
a) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng \(( - \infty ;0)\)?
b) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng \((0; + \infty )\)?
Lời giải chi tiết:
Dựa vào đồ thị, ta thấy:
a) Trên khoảng \(\left( { - \infty ;0} \right)\) , giá trị của f(x) tăng
b) Trên khoảng \(\left( {0; + \infty } \right)\) , giá trị của f(x) giảm
Vẽ đồ thị của hàm số \(y = 3x + 1\) và \(y = - 2{x^2}\). Hãy cho biết:
a) Hàm số \(y = 3x + 1\)đồng biến hay nghịch biến trên \(\mathbb{R}\)
b) Hàm số \(y = - 2{x^2}\)đồng biến hay nghịch biến trên \(( - \infty ;0)\) và \((0; + \infty )\).
Phương pháp giải:
Quan sát đồ thị hàm số trên (a;b)
Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.
Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải.
Lời giải chi tiết:
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)
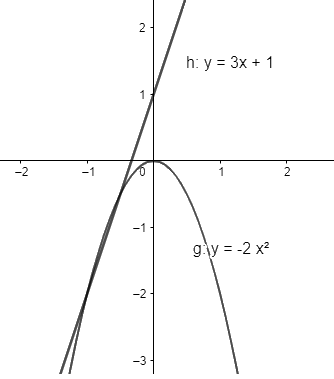
a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.
a) Tính số tiền phải trả khi di chuyển 25 km.
b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.
c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.
Lời giải chi tiết:
Gọi x là số km taxi đã đi; y (nghìn đồng) là số tiền cước phải trả
a) Khi di chuyển 25km thì
Với 0,6km đầu tiên, số tiền cước phải trả 10000 (đồng)
Với những km tiếp theo, số tiền cước phải trả 13000.(25-0,6)=317200(đồng)
Vậy số tiền cước phải trả 317200+10000=327200(đồng)
b) Khi hành khách đi từ 0km đến 0,6km thì \(y = 10\)(nghìn đồng)
Khi hành khách đi từ 0,7km đến 25km thì \(y = 10 + (x - 0,6).13 = 13x + 2,2\)(nghìn đồng)
Khi khách hàng đi từ 25km trở lên \(y = 13.25 + 2,2 + (x - 25).11 = 11x + 52,2\) (nghìn đồng)
c) Vẽ đồ thị hàm số
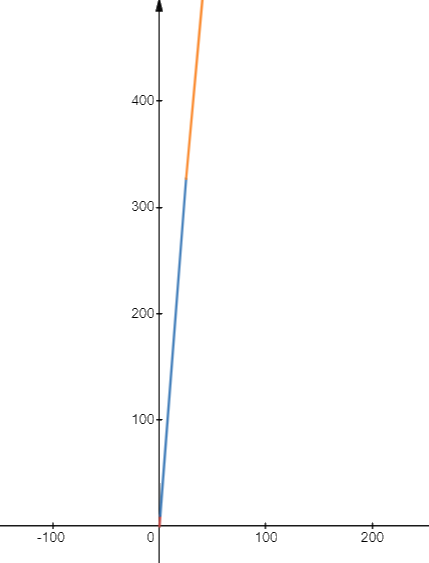
Nhìn trên đồ thị ta có thể thấy đồ thị đồng biến trên \(\left( {0; + \infty } \right)\)
Giải Mục 3 Trang 8 SGK Toán 10 Tập 2 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Mục 3 trang 8 SGK Toán 10 Tập 2 - Kết Nối Tri Thức thường xoay quanh các bài toán liên quan đến vectơ, phép toán vectơ, và ứng dụng của vectơ trong hình học. Để giải quyết các bài toán này một cách hiệu quả, bạn cần nắm vững các khái niệm cơ bản và các công thức liên quan.
1. Khái Niệm Cơ Bản Về Vectơ
Vectơ là một đoạn thẳng có hướng. Nó được xác định bởi điểm gốc và điểm cuối. Vectơ được ký hiệu bằng một chữ cái in hoa hoặc một cặp điểm (ví dụ: AB, a).
- Độ dài của vectơ: Khoảng cách giữa điểm gốc và điểm cuối.
- Hướng của vectơ: Hướng của đoạn thẳng.
- Vectơ chỉ phương: Vectơ có cùng hướng với một đường thẳng.
2. Phép Toán Vectơ
Có hai phép toán cơ bản trên vectơ là phép cộng và phép nhân với một số thực.
- Phép cộng vectơ: Cộng hai vectơ bằng cách cộng các tọa độ tương ứng của chúng.
- Phép nhân vectơ với một số thực: Nhân một vectơ với một số thực bằng cách nhân mỗi tọa độ của vectơ đó với số thực đó.
3. Ứng Dụng Của Vectơ Trong Hình Học
Vectơ được sử dụng để biểu diễn các điểm, đường thẳng, và các hình hình học khác. Nó cũng được sử dụng để giải quyết các bài toán về khoảng cách, góc, và diện tích.
4. Giải Chi Tiết Bài Tập Mục 3 Trang 8
Để giải các bài tập trong Mục 3 trang 8, bạn cần:
- Đọc kỹ đề bài và xác định các thông tin đã cho và yêu cầu của bài toán.
- Vẽ hình minh họa để giúp bạn hiểu rõ hơn về bài toán.
- Sử dụng các khái niệm và công thức liên quan để giải bài toán.
- Kiểm tra lại kết quả của bạn để đảm bảo tính chính xác.
Ví dụ: (Giả sử có một bài tập cụ thể ở trang 8, ở đây sẽ là lời giải chi tiết cho bài tập đó. Ví dụ: Bài 3 trang 8)
Cho tam giác ABC, với A(1;2), B(3;4), C(5;0). Tìm tọa độ của điểm D sao cho ABCD là hình bình hành.
Giải:
Vì ABCD là hình bình hành, ta có: overrightarrow{AB} = overrightarrow{DC}.
overrightarrow{AB} = (3-1; 4-2) = (2; 2)
Gọi D(x; y). Khi đó, overrightarrow{DC} = (5-x; 0-y) = (5-x; -y)
Suy ra: 5-x = 2 và -y = 2. Vậy x = 3 và y = -2. Do đó, D(3; -2).
5. Luyện Tập Thêm
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. tusach.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp bạn tự tin hơn trong quá trình học tập.
6. Tổng Kết
Việc nắm vững các khái niệm cơ bản về vectơ, phép toán vectơ, và ứng dụng của vectơ trong hình học là rất quan trọng để giải quyết các bài tập trong Mục 3 trang 8 SGK Toán 10 Tập 2 - Kết Nối Tri Thức. Hãy luyện tập thường xuyên và tìm kiếm sự giúp đỡ khi cần thiết để đạt được kết quả tốt nhất.
Chúc bạn học tốt!